2020-2021学年14.2 三角形全等的判定图文课件ppt

这是一份2020-2021学年14.2 三角形全等的判定图文课件ppt，共18页。PPT课件主要包含了情境引入，作图与探究，新课讲授，“角边角”判定方法，几何语言，∴DBCB，练一练，证明∵BE＝CF，即BF＝CE，等式性质等内容，欢迎下载使用。

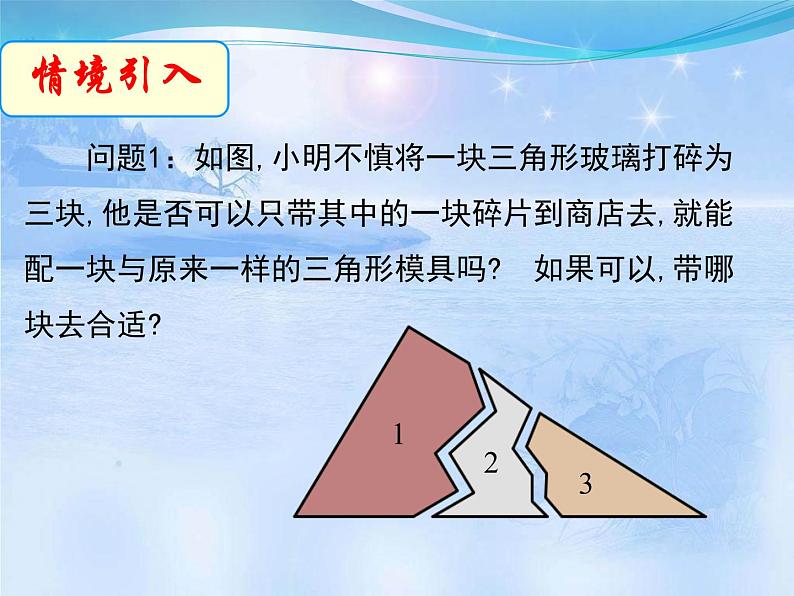
问题1：如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?
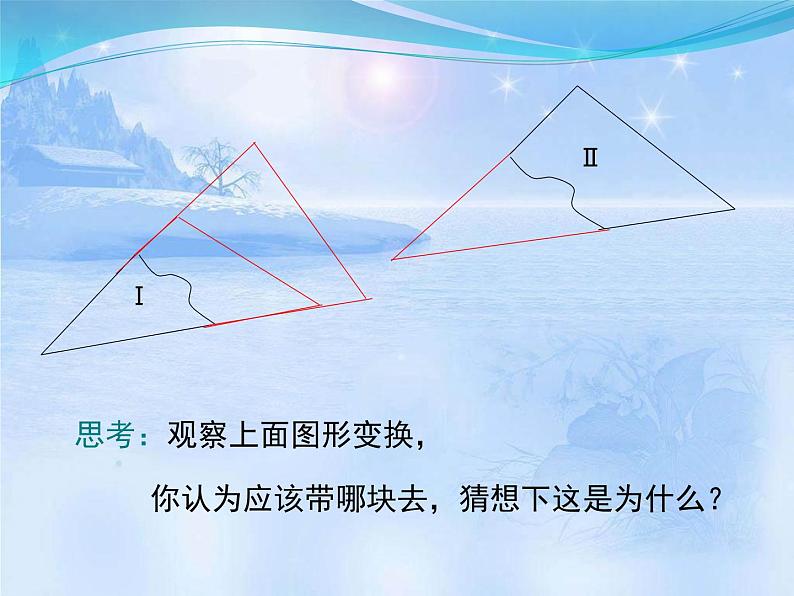
思考：观察上面图形变换，
你认为应该带哪块去，猜想下这是为什么？
活动：猜想、测量、验证
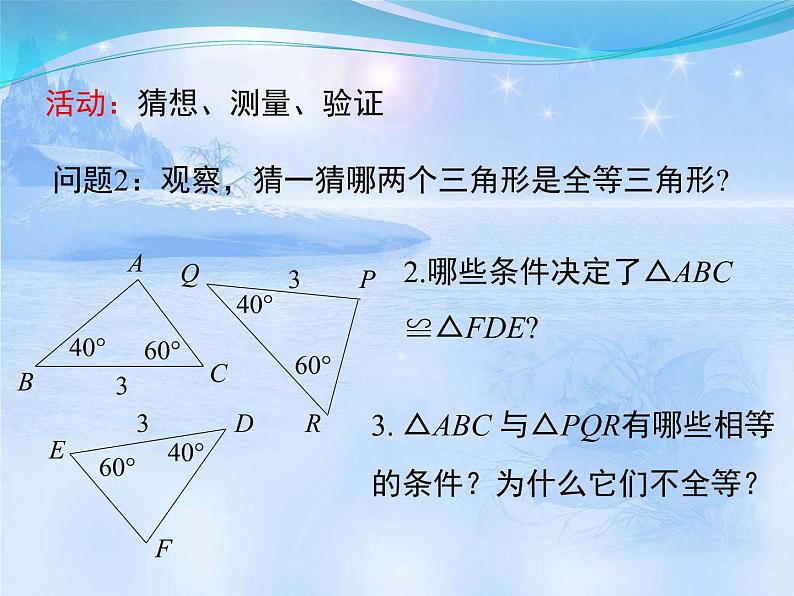
问题2：观察，猜一猜哪两个三角形是全等三角形?
2.哪些条件决定了△ABC ≌△FDE?
3. △ABC 与△PQR有哪些相等的条件？为什么它们不全等？
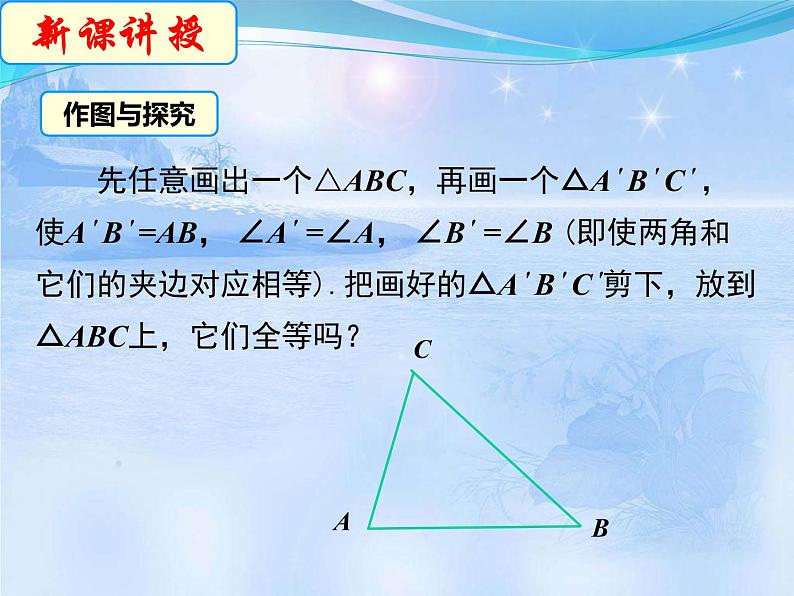
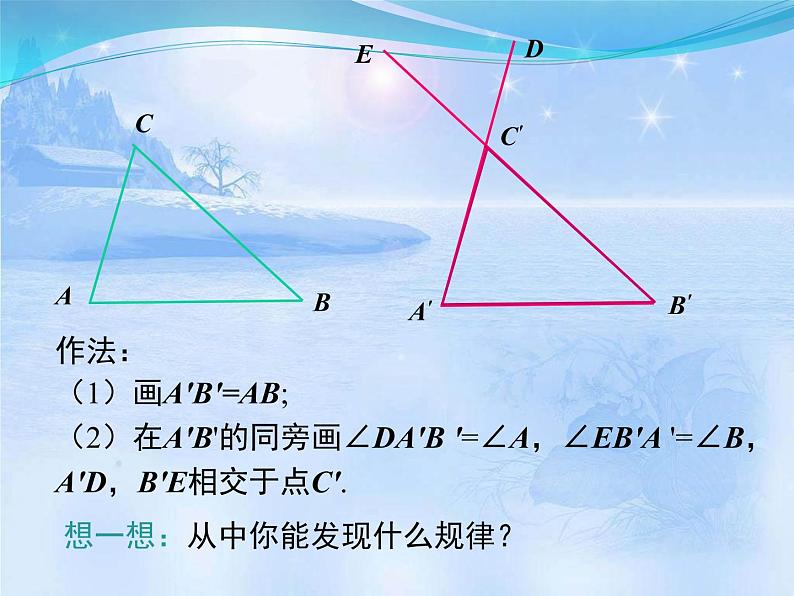
先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ， 使A ′ B ′ =AB， ∠A ′ =∠A， ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下，放到△ABC上，它们全等吗？
作法：（1）画A'B'=AB;（2）在A'B'的同旁画∠DA'B '=∠A，∠EB'A '=∠B，A'D，B'E相交于点C'.
想一想：从中你能发现什么规律？
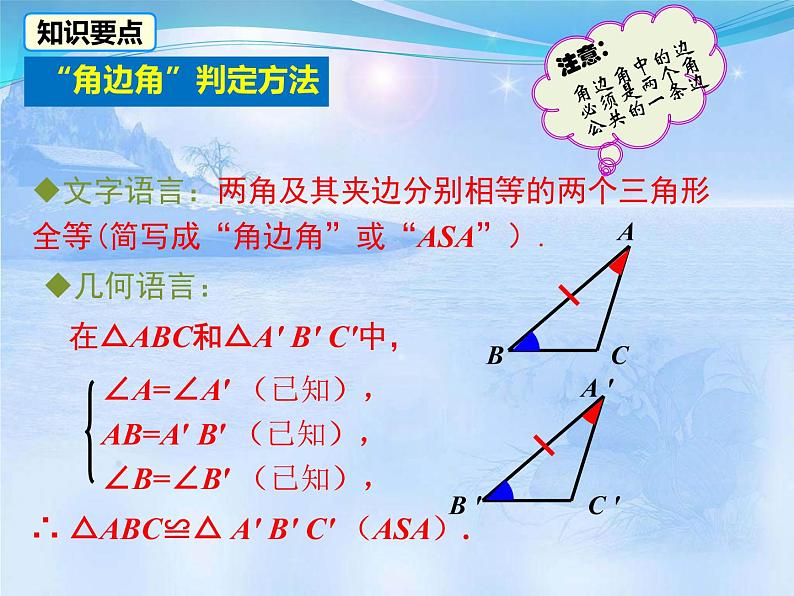
文字语言：两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”）.
注意：角边角中的边必须是两个角公共的一条边
例1 如图， ∠DAB＝ ∠CAB，∠ DBP＝ ∠CBP，求证：DB=CB.
∵ ∠DBA与∠DBP互为邻补角， ∠ABC与∠CBP互为邻补角，
　且∠DBP＝ ∠CBP，
∴ ∠DBA＝∠CBA，（等角的补角相等）
在△ABD和△ABC中，
∠DAB＝ ∠CAB ，（已知）AB=AB，（公共边）∠DBA＝∠CBA，（已证）
∴ △ABD ≌ △ABC（ASA），
（全等三角形的对应边相等）
“ASA”的判定与性质的综合运用
1、如图，点E，F在BC上，BE＝CF，∠AFB＝∠DEC，∠B＝∠C.求证：AB＝DC.
∴BE＋EF＝CF＋EF
在△ABF和△DCE中，
∠B＝∠C （已知） BF＝CE （已证）∠AFB＝∠DEC（已知）
∴△ABF≌△DCE. (ASA)
例2 如图，要测量河两岸相对的两点A、B之间的距离，可以在AB的垂线BF上取两点C、D，使BC=CD，再过点D作BF的垂线DE.使点A、C、E在一条直线上，这时测得DE的长等于AB的长，请说明道理.
已知AB⊥BD，ED ⊥ BD，且AE交BD于C，BC=CD.
2.转化为判定的条件：
∠ ABC=∠EDC=90° (垂直定义）
BC=DC，(已知条件）
∠ ACB=∠ ECD . (对顶角相等）
△ABC≌△EDC(ASA)∴AB=DE(全等三角形的对应边相等）
∵ AB⊥BD，ED ⊥ BD
∴ ∠ ABC=∠EDC=90°
在△ABC和△EDC中，
∠ABC ＝ ∠EDC ，（已证） BC ＝ DC，（已知）∠ACB＝∠ECD，（对顶角相等）
∴ △ABC ≌ △EDC (ASA)
(全等三角形的对应边相等）
如图，已知∠ACB=∠DBC，∠ABC=∠CDB，判别图中的两个三角形是否全等，并说明理由.
不全等，因为BC虽然是公共边，但不是对应边.
易错点：判定全等的条件中，必须是对应边相等， 对应角相等，否则不能判定.
1.如图，如果∠A=∠D, ∠B=∠E，要使△ABC≌△DEF ，需添加一个条件 _______.
2、课本P102练习第2、3题
两角及其夹边分别相等的两个三角形
给出两角的度数和所夹边的长，作三角形，形状是唯一的
三角形全等的“ASA”判定：两角及其夹边分别相等的两个三角形全等.