巩固练习_直线、平面垂直的判定_基础

【巩固练习】

1．下列表述正确的个数为（    ）

①若直线a∥平面，直线a⊥b，则b⊥；

②若直线a平面，b，且a⊥b，则a⊥；

③若直线a平行于平面内的两条直线，则a∥；

④若直线a垂直于平面内两条直线，则a⊥。

A．0    B．1    C．2    D．3

2．若经过直线外的任意一点，作该直线的垂直平面，可作出平面的个数为（    ）

A．1    B．2    C．3    D．无数

3．（2016 浙江）已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则（    ）

A．m∥l    B．m∥n    C．n⊥l    D．m⊥n

4．1，2，3是空间三条不同的直线，则下列命题正确的是（    ）

A．1⊥2，2⊥31∥3

B．1⊥2，2∥31⊥3

C．1∥2∥31，2，3共面

D．1，2，3共点1，2，3共面

5．（2015广东珠海二模）l、m是空间条直线，、是空间两个平面，则（    ）

A．l∥m，，，则

B．l⊥m，，，则

C．，，，则l⊥m

D．，l∥m，，则

6．在三棱柱ABC—A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是（    ）

A．30°    B．45°    C．60°    D．90°

7．如右图，三棱锥P—ABC中，PA⊥平面ABC，∠BAC=90°，则二面角B—PA—C的大小为（    ）

A．90°    B．60°    C．45°    D．30°

8．如图，已知六棱锥P—ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论正确的是（    ）

A．PB⊥AD

B．平面PAB⊥平面PBC

C．直线BC∥平面PAE

D．直线PD与平面ABC所成的角为45°

9．设三棱锥P—ABC的顶点P在平面ABC上的射影是H，给出下列命题：

①若PA⊥BC，PB⊥AC，则H是△ABC的垂心；

②若PA、PB、PC两两互相垂直，则H是△ABC的垂心；

③若∠ABC=90°，H是AC的中点，则PA=PB=PC；

④若PA=PB=PC，则H是△ABC的外心。

则正确命题的序号有________。

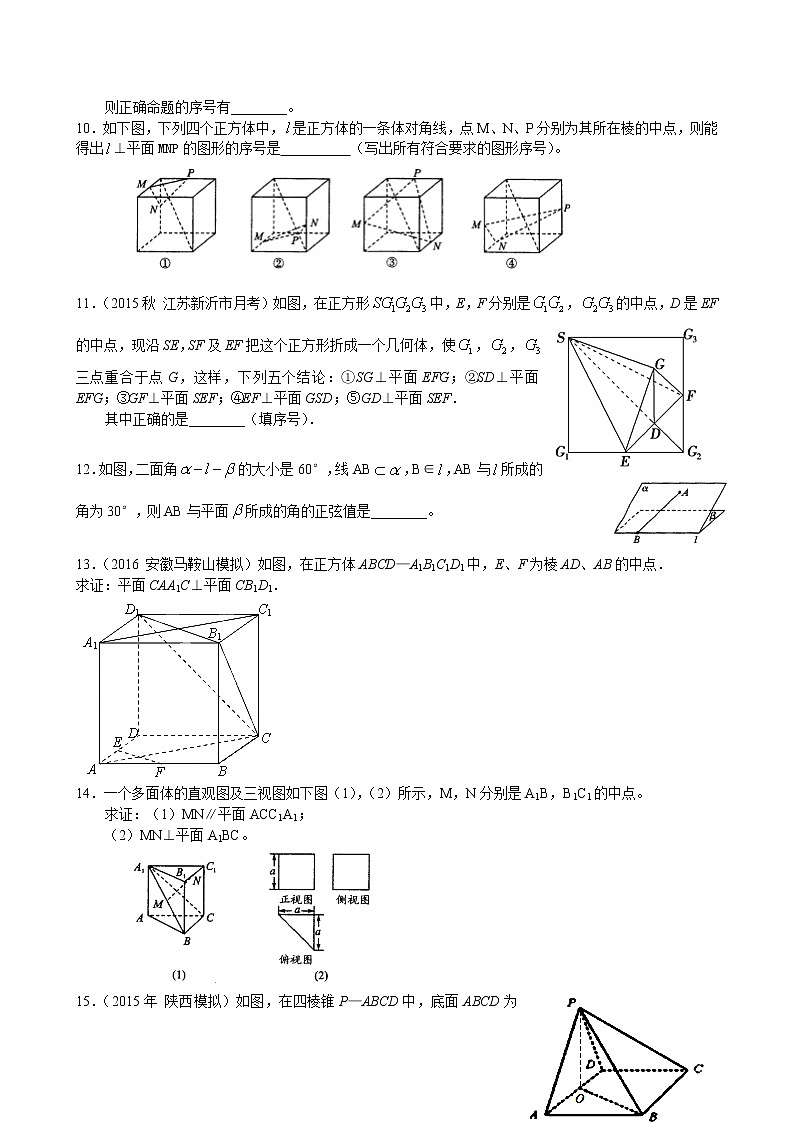
10．如下图，下列四个正方体中，是正方体的一条体对角线，点M、N、P分别为其所在棱的中点，则能得出⊥平面MNP的图形的序号是          （写出所有符合要求的图形序号）。

11．（2015秋 江苏新沂市月考）如图，在正方形中，E，F分别是，的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使，，三点重合于点G，这样，下列五个结论：①SG⊥平面EFG；②SD⊥平面EFG；③GF⊥平面SEF；④EF⊥平面GSD；⑤GD⊥平面SEF．

其中正确的是________（填序号）．

12．如图，二面角的大小是60°，线AB，B∈，AB与所成的角为30°，则AB与平面所成的角的正弦值是________。

13．（2016 安徽马鞍山模拟）如图，在正方体ABCD—A1B1C1D1中，E、F为棱AD、AB的中点．

求证：平面CAA1C⊥平面CB1D1．

14．一个多面体的直观图及三视图如下图（1），（2）所示，M，N分别是A1B，B1C1的中点。

求证：（1）MN∥平面ACC1A1；

（2）MN⊥平面A1BC。

15．（2015年 陕西模拟）如图，在四棱锥P—ABCD中，底面ABCD为菱形且∠DAB=60°，O为AD中点．

（1）若PA=PD，求证：平面POB⊥平面PAD；

（2）试问在线段BC上是否存在点M，使DM∥面POB，如存在，指出M的位置，如不存在，说明理由．

16．如右图，在三棱锥A—BCD中，AB⊥平面BCD，BD⊥CD。

（1）求证：平面ABD⊥平面ACD；

（2）若AB=BC=2BD，求二面角B—AC—D的正切值。

【答案与解析】

1．【答案】A

【解析】 ①中b与还可能平行、斜交或b在平面内；②中a与还可能平行或斜交；③中a还可能在平面内；由直线与平面垂直的判定定理知④错。

2．【答案】A

【解析】  过直线外的一点与一个平面垂直的平面有且仅有一个。

3．【答案】C

【解析】∵互相垂直的平面α，β交于直线l，直线m，n满足m∥α，

∴m∥β或mβ或m与β相交，，

∵n⊥β，

∴n⊥l．

故选：C．

4．【答案】B

【解析】  在空间中，垂直于同一直线的两条直线不一定平行，故A错；两平行线中的一条垂直于第三条直线，则另一条也垂直于第三条直线，B正确；相互平行的三条直线不一定共面，如三棱柱的三条侧棱，故C错；共点的三条直线不一定共面，如三棱锥的三条侧棱，故D错。

5．【分析】根据空间直线和平面平行或垂直的判定定理以及性质定理分别进行判断即可．

【答案】D

【解析】A．若l∥m，，，则或与相交，故A错误

    B．若l⊥m，，，则或与相交，故B错误

C．若，，，则l⊥m或l，m相交，或异面直线，故C错误

D．若，l∥m，则，∵，∴成立，故D正确．

故选：D

6．【答案】C

【解析】 如图是三棱柱ABC—A1B1C1，不妨设各棱长为1。

取BC的中点E，连接AE，DE，∵CC1⊥底面ABC，

∴侧面BB1C1C⊥底面ABC，

又E为BC的中点，且△ABC为正三角形，∴AE⊥BC，

由两平面垂直的性质定理知，AE⊥平面BB1C1C，

∴∠ADE的大小就是AD与平面BB1C1C所成角的大小。

容易计算∠ADE=60°。故选C。

7．【答案】A

【解析】 因为PA⊥平面ABC，BA、CA平面ABC，所以BA⊥AP，CA⊥AP，因此，∠BAC即为二面角B—PA—C的平面角，又∠BAC=90°，故选A。

8．【答案】D

【解析】  ∵PA⊥平面ABC，∴∠ADP是直线PD与平面ABC所成的角。

∵六边形ABCDEF是正六边形，∴AD=2AB，

∵，

∴直线PD与平面ABC所成的角为45°，选D。

9．【答案】①②③④ 

【解析】根据线面垂直的判定及定义可证明。

10．【答案】①④ 

【解析】根据线面垂直的判定。

11．【分析】根据题意，在折叠过程中，始终有⊥，⊥，即SG⊥GE，SG⊥GF，由线面垂直的判定定理，易得SG⊥平面EFG，分析四个选项，即可给出正确的选择．

【答案】①

【证明】∵在折叠过程中，始终有SG1⊥，⊥，

即SG⊥GE，SG⊥GF，

∴SG⊥平面EFG．

故答案为：①．

【点评】本题主要考查了垂直问题的证明，其一般规律是“由已知想性质，由求证想判定”，也就是说，根据已知条件去思考有关的性质定理；根据要求证的结论去思考有关的判定定理，往往需要将分析与综合的思路结合起来．

12．【答案】 

【解析】如图，作AO⊥于O，AC⊥于C，连接OB、OC，则OC⊥。

设AB与所成角为，则∠ABO=，

由图得。

13．【解析】因为在正方体中，

⊥平面，而平面，

所以⊥．

又因为在正方形中，⊥，

所以⊥平面．

又因为平面，

所以平面⊥平面．

14．证明：由题意知，该几何体是一个三棱柱，且侧棱与底面垂直，其中AC⊥BC，AC=BC=CC1。

（1）由已知AA1⊥平面A1B1C1，所以AA1⊥A1B1，因此四边形ABB1A1为矩形，连接AB1，则A，M，B1三点共线，且M是AB1的中点。连接AC1，在△AB1C1中，M，N分别为AB1，B1C1的中点，所以MN∥AC1。因为AC1平面ACC1A1，MN平面ACC1A1，所以MN∥平面ACC1A1。

（2）因为AC⊥BC，BC⊥CC1，AC∩CC1=C，所以BC⊥平面ACC1A1，所以BC⊥AC1，又四边形ACC1A1为正方形，所以AC1⊥A1C。又BC∩A1C=C，因此AC1⊥平面A1BC，又MN∥AC1，所以MN⊥平面A1BC。

15．【分析】（1）由题意可证明PO⊥AD，OB⊥AD，从而可证AD⊥面POB，又AD面PAD从而可证面POB⊥面PAD．

   （2）取M为PC的中点，则BMDO为平行四边形，可证DM∥OB，从而可证DM∥面POB．

【解析】（1）∵PA=PD，O为AD中点，∴PO⊥AD

又∵ABCD为菱形且∠DAB=60°，∴OB⊥AD

∵PO∩OB=O，∴AD⊥面POB

∵AD面PAD，∴面POB⊥面PAD

（2）存在，M为BC的中点．

证明如下：BMDO为平行四边形，

故DM∥OB，而OB面POB，DM面POB，

所以，DM∥面POB．

16．【解析】（1）∵AB⊥平面BCD，CD平面BCD，∴AB⊥CD。

又BD⊥CD，且BD∩AB=B，∴CD⊥平面ABD。

又CD平面ACD，∴平面ABD⊥平面ACD。

（2）如图，过D作DE⊥BC于E，由AB⊥DE知，

DE⊥平面ABC，∴DE⊥AC。

过E作EF⊥AC于F，连接DF，∴AD⊥平面DEF，则AC⊥DF，

∴∠DFE就是二面角B—AC—D的平面角。

设BD=x，则AB=BC=2x。

在Rt△BDC中，

，BD·CD=BC·DE，则，，。

由Rt△CEF∽Rt△CAB，得，∴，

∴在Rt△DEF中，。

故二面角B—AC—D的正切值为。