期末模拟试题一 安徽省利辛县西关学校2021-2022学年八年级上册数学（沪科版）（word版 含答案）

期末模拟试卷一

姓名：               分数：              

说明：本试题共八大题23小题，总计150分，时间120min

一、选择题（本大题共10小题，每小题4分，总计40分）

1．如图所示，笑脸盖住的点的坐标可能为（    ）

A．（5，2） B．（﹣2，3） 

C．（﹣4，﹣6） D．（3，﹣4）

2．下列四个图案中是轴对称图形的是（　　）

A．B．C． D．

3．等腰三角形底边长为，一腰上的中线把其周长分为两部分的差为．则等腰三角形的腰长为（    ）

A． B．

C．或 D．以上答案都不对

4．下列说法不正确的是（     ）

A．对顶角相等 B．两点确定一条直线

C．一个角的补角一定大于这个角 D．垂线段最短

5．已知点，，都在直线上，则，，的大小关系是（    ）

A． B． 

C． D．

6．如图，已知，添加下列条件，不能判定的是（    ）

A． B．

C． D．

7．如图，已知在四边形中，，平分，，，，则四边形的面积是（  ）

A．24   B．30   C．36    D．42

8．直线和在同一平面直角坐标系中的图象可能是（    ）

A． B． 

C． D．

9．如图，在边长为4的等边△ABC中，点P从A点出发，沿A→B→C→A的方向运动，到达A点时停止．在此过程中，线段AP的长度y随点P经过的路程x的函数图象大致是（　　）

A． B．

C． D．

10．如图，已知，点D、E分别在、上且，连接交于点M，连接，过点A分别作，垂足分别为F、G，下列结论：①；②；③平分；④如果，则E是的中点；其中正确结论的个数为（    ）

A．1个 B．2个 

C．3个 D．4个

二、填空题（本大题共4小题，每小题5分，总计20分）

11．式子有意义，则a的取值范围是_________．

12．若a＝b，则，则它的逆命题是________________，该命题是填（“真、假”）命题：___．

13．如图，一次函数y＝kx+b（k、b为常数，且k≠0）与正比例函数y＝ax（a为常数，且a≠0），则不等式kx+b≤ax的解集是___．

14．在平面直角坐标系xOy中，若直线y＝2x＋3向下平移n个单位长度后，与直线y＝﹣x＋2的交点在第一象限，则n的取值范围是________．

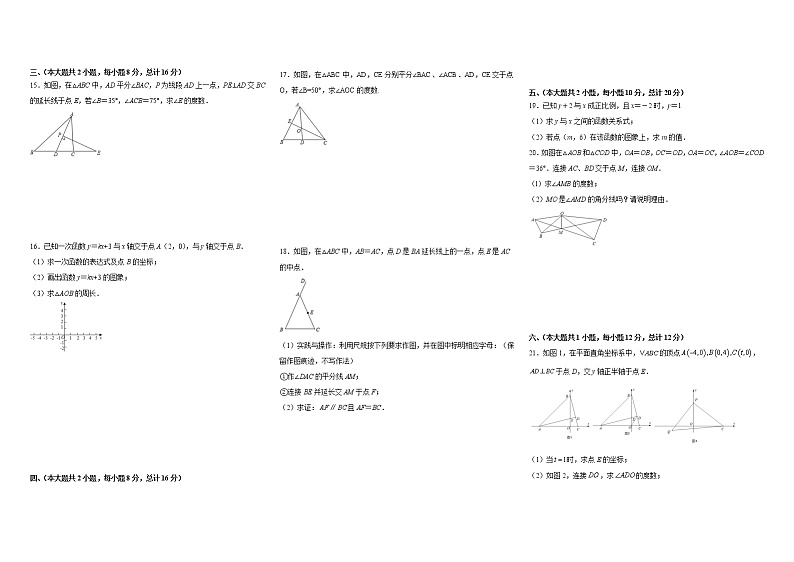
三、（本大题共2小题，每小题8分，总计16分）

15．如图，在△ABC中，AD平分∠BAC，P为线段AD上一点，PE⊥AD交BC的延长线于点E，若∠B＝35°，∠ACB＝75°，求∠E的度数．

16．已知一次函数y＝kx+3与x轴交于点A（2，0），与y轴交于点B．

（1）求一次函数的表达式及点B的坐标；

（2）画出函数y＝kx+3的图象；

（3）求△AOB的周长．

四、（本大题共2小题，每小题8分，总计16分）

17．如图，在△ABC中，AD，CE分别平分∠BAC、∠ACB．AD，CE交于点O，若∠B=50°，求∠AOC的度数.

18．如图，在△ABC中，AB＝AC，点D是BA延长线上的一点，点E是AC的中点．

（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母：（保留作图痕迹，不写作法）

①作∠DAC的平分线AM；

②连接BE并延长交AM于点F；

（2）求证：且AF＝BC．

五、（本大题共2小题，每小题10分，总计20分）

19．已知y＋2与x成正比例，且x＝－2时，y＝1

（1）求y与x之间的函数关系式；

（2）若点（m，6）在该函数的图象上，求m的值．

20．如图在△AOB和△COD中，OA＝OB，OC＝OD，OA＝OC，∠AOB＝∠COD＝36°．连接AC、BD交于点M，连接OM．

（l）求∠AMB的度数；

（2）MO是∠AMD的角分线吗？请说明理由．

六、（本大题共1小题，每小题12分，总计12分）

21．如图1，在平面直角坐标系中，的顶点，于点D，交y轴正半轴于点E．

（1）当时，求点E的坐标；

（2）如图2，连接，求的度数；

（3）如图3，已知点，若，求Q的坐标（用含t的式子表示）．

七、（本大题共1小题，每小题12分，总计12分）

22．我市某著名景点门票价格规定如下表：

小明妈妈的公司有一项短途旅行业务，就是去该景点一日游．学完一元一次方程以后，他妈妈让他给规划一个去该景点游玩的购票方案，给他的提示是：有甲、乙两个团队共32人，其中甲团队3人以上，不足10人．经估算，如果两个团队分别购票，则应付门票费2100元．

（1）两个团队各有多少人？

（2）如果两个团队联合起来，作为一个团体购票，可省钱      元．

（3）如果乙团队临时有事不能去了，只有甲团队单独去游玩，通过计算说明如何购票最省钱？

八、（本大题共1小题，每小题14分，总计14分）

23．（问题）在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且∠EAF＝60°，试探究图1中线段BE、EF、FD之间的数量关系．

(1)（探索）有同学认为：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE、EF、FD之间的数量关系是        ．

(2)（延伸）在四边形ABCD中如图2，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，∠EAF＝∠BAD，上述结论是否仍然成立？说明理由．

(3)（构造运用）如图3，在某次搜救行动中，甲艇在指挥中心（O处）北偏西30°的A处，乙艇在O点的南偏东70°的B处，且AO＝BO，接到行动指令后，甲艇向正东方向以60海里/小时的速度前进，乙艇沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，甲、乙两艇分别到达E，F处，∠EOF＝70°，试求此时甲、乙两艇之间的距离．

参考答案

1．D

2．D

3．B

4．C

5．A

6．C

7．B

8．B

9．A

10．D

11．a≥1且a≠2

12．如果，那么    假   

13．x2．

14．1＜n＜7

15．

解：∵，，

∴，

∵AD平分∠BAC，

∴，

∴，

∵PE⊥AD，

∴，

∴．

16．

解：（1）∵一次函数经过点A（2，0），

∴，

∴，

∴一次函数解析式为，

∵B是一次函数与y轴的交点，

∴B点坐标为（0，3）；

（2）列表如下：

函数图像如下所示：

（3）∵A点坐标为（2，0），B点坐标为（0，3），

∴OA=2，OB=3，

∴，

∴△AOB的周长．

17．

∵AD，CE分别平分∠BAC、∠ACB，

∴∠DAC=∠BAC，∠ACE=∠ACB，

∵∠B=50°，

∴∠BAC+∠ACB=180°-∠B=130°，

∴∠DAC+∠ACE=（∠BAC+∠ACB）=65°，

∴∠AOC=180°-（∠DAC+∠ACE）=115°.

18．

解：（1）如图所示，AM即为所求，BE的延长线交AM于F．

（2）证明：∵AB＝AC，

∴∠ABC＝∠C，

∴∠DAC＝∠ABC+∠C＝2∠C，

∠DAC的平分线AM，

∵∠DAC＝2∠FAC，

∴∠C＝∠FAC，

∴，

∵E是AC中点，

∴AE＝EC，

在△AEF和△CEB中，

，

∴△AEF≌△CEB，

∴AF＝BC．

19．

解：（1）∵与成正比例

∴设

将，代入得，即

∴，即

∴与之间的函数关系式为；

（2）∵点（，）在该函数图象上

将其代入到中有，解得

∴的值是

20．

解：（1）令OB与AC交于点N，

∵∠AOB＝∠COD＝36°，

∴ ，

即 ，

∵OA＝OB，OC＝OD，

∴ ，

∴ ，

∵ ，

∴ ，

（2）作OG⊥AM于G，OH⊥DM于H，

∴ ，

由（1）知，

∴， ，

∵

∴ ，

∴MO是∠AMD的角分线（角平分线上一点到两边距离相等）．

21．解：（1）∵AD⊥BC，   

∴∠EAO+∠BCO=90°，

∵∠CBO+∠BCO=90°，

∴∠EAO=∠CBO，

在△AOE和△BOC中，

∵，

∴△AOE≌△BOC（ASA），

∴OE=OC=1，

∴点E坐标（0，1）．

（2）如图2，过点O作OM⊥AD于点M，作ON⊥BC于点N，

∵△AOE≌△BOC，

∴S△AOE=S△BOC，且AE=BC，

∵OM⊥AE，ON⊥BC，

∴OM=ON，

∴OD平分∠ADC；

AD⊥BC

∴∠ADO=；

（3）如图3，过P作GH//x轴，过C作CG⊥GH于G，过Q作QH⊥GH于H，交x轴于F，

∵P（0，3），C（t，0），

∴CG=FH=3，PG=OC=t，

∵∠QPC=90°，

∴∠CPG+∠QPH=90°，

∵∠QPH+∠HQP=90°，

∴∠CPG=∠HQP，

在△PCG和△QPH中，

，

∴△PCG≌△QPH（AAS）,

∴CG=PH=3，PG=QH=t，

∴Q（-3，3-t）．

22．

解：（1）设甲团队有x人，

由题意可知，乙团队人数大于20人小于30人，列方程得

解方程，得

这时，

答：甲团队有9人，乙团队有23人．

（2）由题意得人数一共有32人，则合买的花销 元，

∴可省钱2100-1600=500元

故答案为：500；

（3）直接购买：（元）；

按团体票购买：（元）

∵720＞660，

∴购买11张票最省钱．

答：购买11张票最省钱．

23

解：(1)【探索】EF=BE+FD，

证明：如图，延长FD到G，使DG=BE，连接AG，

∵∠B=∠ADC=90°，∠ADG=∠ADC=90°，

∴∠B=∠ADG，

在△ABE和△ADG中，

，

∴△ABE≌△ADG（SAS），

∴AE=AG，∠BAE=∠DAG，

∵∠EAF=60°，∠BAD=120°，

∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF=60°，

∴∠EAF=∠GAF，

在△AEF和△AGF中，

，

∴△AEF≌△AGF（SAS），

∴EF=FG，

∴FG=DG+FD=BE+DF；

故答案为：EF=BE+FD，

(2)【延伸】结论仍然成立，

证明：如图2，延长FD到G，使DG=BE，连接AG，

∵∠B+∠ADC=180°，∠ADG+∠ADC=180°，

∴∠B=∠ADG，

在△ABE和△ADG中，

，

∴△ABE≌△ADG（SAS），

∴AE=AG，∠BAE=∠DAG，

∵∠EAF=∠BAD，

∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF，

∴∠EAF=∠GAF，

在△AEF和△AGF中，

，

∴△AEF≌△AGF（SAS），

∴EF=FG，

∴FG=DG+FD=BE+DF；

(3)【构造运用】解：如图3，连接EF，延长AE、BF交于点C，

∵∠AOB=30°+90°+（90°﹣70°）=140°，

∠EOF=70°，

∴∠EOF=∠AOB，

∵OA=OB，

∠OAC+∠OBC=（90°﹣30°）+（70°+50°）=180°，

∴符合探索延伸中的条件

∴结论EF=AE+BF成立，

即EF=1.5×（60+80）=210海里，

答：此时两舰艇之间的距离是210海里．