高中数学人教版新课标B必修31.2.3循环语句教案及反思
展开剖析两种循环语句
在实际应用中,经常会遇到许多有规律性的重复运算,对于这类问题的解决就必须依靠循环结构程序设计,而循环结构是由循环语句来实现的,Scilab中有for型与while型两种语句结构,即for语句与while语句,具体剖析如下:
1.for语句的一般格式是:
剖析:对于for型循环结构,计算机执行语句时先将初值赋给左边的变量(称为循环控制变量),然后判断循环控制变量的值是否已“超过”终值,如已超过,则跳过循环体执行end后面的语句,如未超过终值,则执行循环体,遇到end,循环变量加一个步长,赋给左边的变量,进行前面的重复.现举例说明如下:
例1 编程求S=1×2×3×…×n,这里的n不大于100.
解:(1)设计算法如下:
S1:S=1;i=2;
S2:若i≤100,则S=S×i;i=i+1,重复S2;否则执行S3.
S3:输出S.
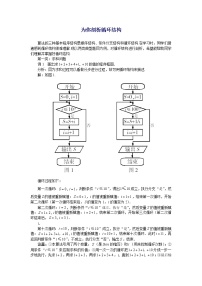
(2)根据算法画出程序框图:
(3)根据程序框图编写程序:
S=1;
for i=2∶1∶100
S=Si;
end
print(%io(2),S)
2.while语句的一般格式是:
剖析:当计算机遇到while语句时,先判断条件的真假,如果条件符合,就执行while与end之间的循环体,然后再检查上述条件,如果仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止,这时计算机将不再执行循环体,而是跳到end语句后,接着执行end后面的语句.现举例说明如下:
例2 编程求1×3×5×…×n>10000的最小正整数n.
解:(1)设计算法如下:
S1:S=1;i=1.
S2:若S≤10000,则i=i+2;S=S×i;重复S2,否则执行S3.
S3:输出i.
(2)根据算法画出程序框图:
(3)根据框图编写程序:
S=1;i=1;
while S<=10000
i=i+2;
S=Si;
end
print(%io(2),i)
通过以上对for语句与while语句的剖析,可以看出:for语句适用于预先知道循环次数的循环结构,而while语句首先要对表达式进行判断,适用于任何的循环结构,如:例1在Scilab语言中又可用while语句编写为:
S=1;i=2;
while i<=100
S=Si;
i=i+1;
end
print(%io(2),S)
总之,循环语句主要用来实现算法中的循环结构,在处理一些需要反复执行的运算任务,如累加求和,累乘求积等问题中常用到.在用for语句和while语句编写程序解决问题时,一定要注意它们的格式及条件的表述方法.
高中数学人教版新课标B必修31.2.3循环语句教学设计: 这是一份高中数学人教版新课标B必修31.2.3循环语句教学设计,共5页。教案主要包含了知识与技能,过程与方法,情态与价值等内容,欢迎下载使用。
高中数学人教版新课标B必修31.2.3循环语句教学设计: 这是一份高中数学人教版新课标B必修31.2.3循环语句教学设计,共4页。教案主要包含了教学目标,教学的重点,教学方法与手段,教学过程等内容,欢迎下载使用。
数学1.2.3循环语句教案: 这是一份数学1.2.3循环语句教案,共9页。