

高中数学人教版新课标B必修31.2.3循环语句教案
展开
基本算法语句
重点难点
重点:正确理解循环语句的概念,并掌握其结构;会应用循环语句编写程序;并能进行简单的综合应用。
难点:理解循环语句的表示方法、结构和用法;会编写程序中的循环语句.
【学习导航】
知识网络
循环语句→当型循环语句
学习要求
1.正确理解循环语句的概念,并掌握其结构;会应用循环语句编写程序;并能进行简单的综合应用。
2.理解并掌握循环语句在计算机程序语言中的作用,掌握两种循环语句应用的实例:数列求和、求积。
【课堂互动】
自学评价
1.问题:
设计计算的一个算法。
【分析】将上述表达式看成49个乘法,用公式表示为:
S←S×I
S初始为1,I为1,将每次的乘积都赋予S,I从1到99,每次增加2,公式S←S×I会被重复执行,这种执行过程可用循环结构表示。
算法一:
S1 S←1;
S2 I←1;
S3 I←I+2;
S4 S←S×I;
S5 如果I小于99,那么转S3;
S6 输出S
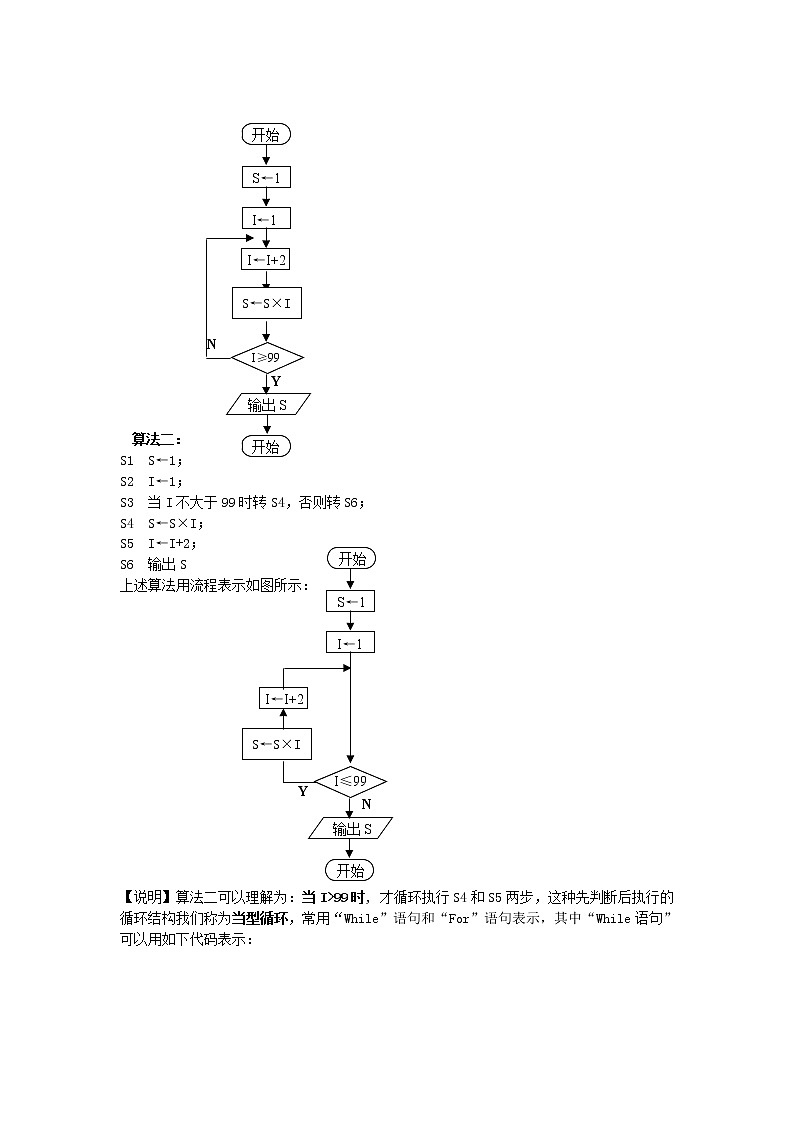
上述算法用流程图表示如下:
【说明】算法一是先执行后判断的直到型循环结构,常用“Do”语句表示,我们不再学习。
算法二:
S1 S←1;
S2 I←1;
S3 当I不大于99时转S4,否则转S6;
S4 S←S×I;
S5 I←I+2;
S6 输出S
上述算法用流程表示如图所示:
【说明】算法二可以理解为:当I>99时, 才循环执行S4和S5两步,这种先判断后执行的循环结构我们称为当型循环,常用“While”语句和“For”语句表示,其中“While语句”可以用如下代码表示:
用伪代码表示为:
S←1
I←1
While I≤99
S←S×I
I←I+2
End While
Print S
由此可见,同一个问题可以用不同的循环方式来解决,直到型循环和当型循环的控制条件是不同的,请注意流程图中判断分支的流向条件。
在算法二的伪代码中,可以看成I从1到99,每次增加2,用For语句写成I From 1 To 99 Step 2,“Step 2”意为I每次增加2。写成一般形式为:
注意黑体字部分是For循环语句的关键词,在“For”和“End For”之间的步骤称为循环体,如果省略“Step 2”,那么循环时I的值默认增加1。
上述问题用For循环语句的伪代码可以表示为:
S←1
For I From 1 To 99 Step 2
S←S×I
End For
Print S
【总结】当循环的次数确定时,我们通常用For循环语句,而当循环的次数不确定时,我们通常用While循环语句,这两种语句都是前测试语句,即先判断后执行。若初始条件不成立,则一次也不执行循环体中的内容,任何一种需要重复处理的问题都可以用这种前测试循环来实现。
【经典范例】
例1 分别用While语句和For语句写出求1+2+3+…+100的和的一个算法。
【解】用伪代码表示为:
S←0
For I From 1 To 100
S←S+I
End For
Print S
或:
S←0
While I≤100
S←S+I
I←I+1
End While
Print S
【注意】在累加的算法中,S的初始值一般设为0,在累乘的算法中,S的初始值一般设为1,为什么?
例2 问题:将前面的问题改为
>1 0000,那么,如何寻找满足条件的最小整数呢?请用伪代码写出一个算法。
【分析】这个问题中,因为不知道循环需要进行的次数,所以不能用For循环语句。
【解】算法:
S1 S←1;
S2 I←1;
S3 如果S≤10000,那么I←I+2,S←S×I,重复S3;
S4 输出I。
上述算法可以理解为:当S≤10000时,循环执行S3。
伪代码如下:
S←1;
I←1
While S≤10000
S←S×I
I←I+2
End While
Print I
在“For”语句中,I的变化是通过“Step”设置的,在程序运行时自动改变,所以循环体中没有如“I←I+2”这样的语句,而在“While”语句中,则需要手工编写如“I←I+2”这样的代码以控制程序的运行,避免出现“死循环”。
例3 抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先做出确定的判断是不可能的,但是假如硬币的质量均匀,那么当抛掷次数很多时,出现正、反面的机率都应接近于50%,试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出现正面的机率。
分析:抛掷硬币的过程实际上是一个不断重复的地做同一件事情的过程,这样的过程我们可以通过循环语句模拟。
在程序语言中,有一个随机函数“Rnd”,它能产生0与1之间的随机数,这样,我们可以用大于0.5的随机数表示出现正面,不大于0.5的随机数表示出现反面,
【解】用伪代码表示为:
S←0 {求累计和,初始值设为0}
Read n
For I From 1 To n
If Rnd>0.5 Then S←S+1
End For
Print 出现正面的频率为
{单行条件语句不需要结束标志“End If”}
追踪训练
1.下面的伪代码中,“For”语句的循环体是__________________________.
【解】循环体是
S←2S+3,
If S>20 Then
S←S-20
End If
2.我们曾研究过问题 >2 004,试用“While”语句描述这一问题的算法过程。
【解】
S←0
I←1
While S≤2004
S←S+I
I←I+1
End While
Print I
3.2000年我国人口数约为13亿,如果每年的人口自然增长率为15‰,那么多少年后我国人口数将达到或超过15亿?
这个问题可通过循环方式计算完成,即每一次在原有的基础上增加15‰,直到达到或超过15亿,再记下循环次数,试用循环语句表示这一过程。
【解】
s←1300000000
i←0
while s≤1500000000
s←s×(1+0.015)
i←i+1
End While
Print i
4. 1,1,2,3,5,8,13,…这一列数的规律是:第1、第2个数是1,从第3个数起,该数是其前面2个数之和,试用循环语句描述计算这列数中前20个数之和的算法.
【解】
a←1
b←1
S←2
For n From 3 To 20
c←a+b
S←S+c
a←b
b←c
End For
Print S
高中数学1.2.3循环语句教学设计: 这是一份高中数学1.2.3循环语句教学设计,共3页。教案主要包含了教学目标,教学的重点,教学方法与手段,教学过程等内容,欢迎下载使用。
高中数学人教版新课标B必修31.2.3循环语句教学设计: 这是一份高中数学人教版新课标B必修31.2.3循环语句教学设计,共5页。教案主要包含了知识与技能,过程与方法,情态与价值等内容,欢迎下载使用。
高中数学人教版新课标B必修31.2.3循环语句教案及反思: 这是一份高中数学人教版新课标B必修31.2.3循环语句教案及反思,共3页。教案主要包含了教材分析,教学目标分析,教学方法与手段分析,教学过程分析等内容,欢迎下载使用。













