2022届新教材高中数学人教A版数系的扩充与复数的引入单元测试含答案20

2022届新教材人教A版  数系的扩充与复数的 引入   单元测试

一、选择题

1、复数（　　）

A． B． C．i D．2

2、已知复数满足：，则的虚部是（    ）

A．－2 B．2 C． D．

3、使复数为实数的充分而不必要条件的是（    ）

A.为实数 B.为实数 C. D.

4、若，则（   ）

A. B. C. D.

5、关于复数，下列命题①若，则；②为实数的充要条件是；③若是纯虚数，则；④若，则.其中真命题的个数为（    ）

A.1 B.2

C.3 D.4

6、已知是虚数单位，是的共轭复数，若，则的虚部为（    ）

A.  B.  C.  D.

7、已知复数，则下列说法正确的是（  ）

A．复数的实部为3 B．复数的虚部为

C．复数的共轭复数为 D．复数的模为1

8、若为第二象限角．则复数 （为虚数单位）对应的点在（　　）

A.第一象限 B.第二象限 C.第三象限 D.第四象限

9、

已知为虚数单位,若复数满足.则的虚部是（    ）

A．-2    B．4    C．3    D．-4

10、若复数z满足，则z的实部为(     )

A.1 B. C.2 D.

11、若是虚数单位,在复平面内复数表示的点在（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

12、已知复数满足，其中是虚数单位，则复数的虚部为（    ）

A.2 B.-2 C.1 D.-1

二、填空题

13、设复数满足则_______.

14、已知复数满足，则___________.

15、已知复数满足，则________

16、复数的实部为_______.

三、解答题

17、（本小题满分10分）已知，设，当为何值时：

（1）在复平面上对应的点在第二象限？

（2）在复平面上对应的点在直线上.

18、（本小题满分12分）已知复数，，且满足是实数，求实数及的值.

19、（本小题满分12分）已知复数是虚数单位）.

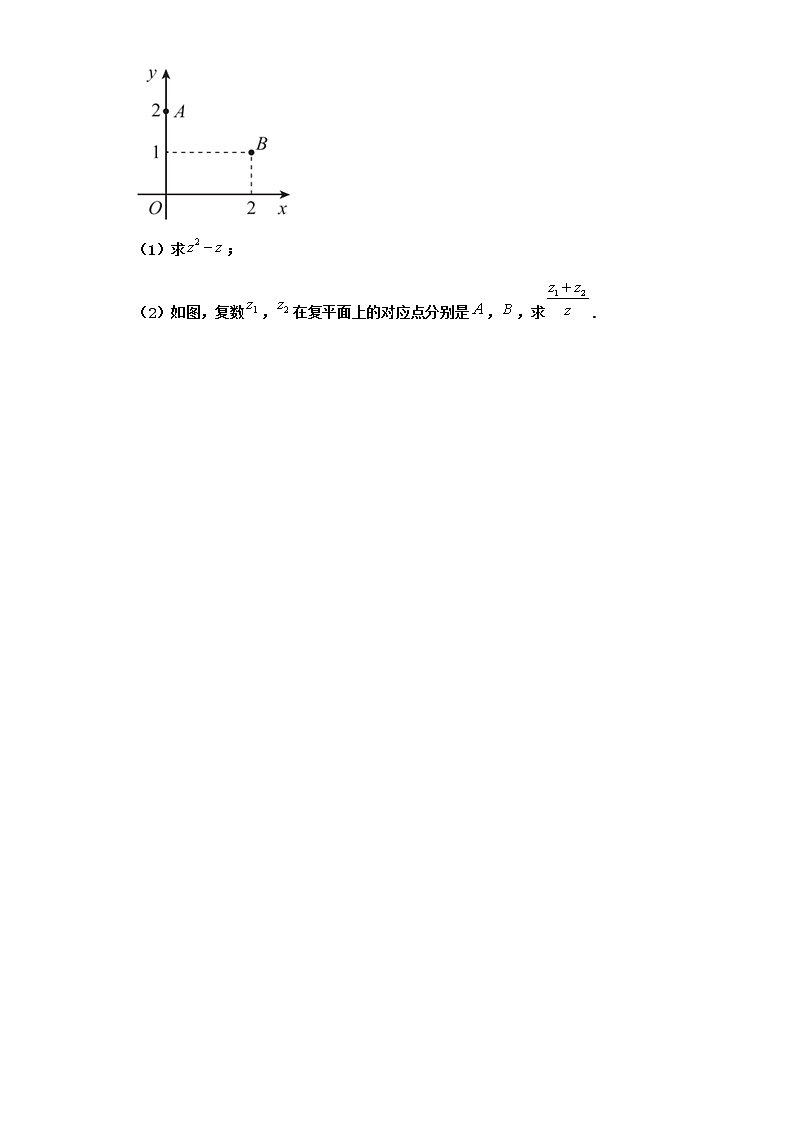
（1）求；

（2）如图，复数，在复平面上的对应点分别是，，求.

参考答案

1、答案A

解析.

故选：A

2、答案B

解析利用复数的除法运算化为的形式，则答案可求．

详解

解：由，得，

则复数z的虚部是2，

故选：B．

点睛

本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

3、答案D

解析一个复数为实数的充分必要条件是它的虚部为0，根据这个充要条件对各个项加以判别，发现A、B都没有充分性，而C是充分必要条件，由此不难得出正确的选项．

详解

解：设复数（是虚数单位），则

复数为实数的充分必要条件为

由此可看出：

对于A，为实数，可能是纯虚数，没有充分性，故不符合题意；

对于B，同样若是纯虚数，则为实数，没有充分性，故不符合题意；

对于C，若等价，故是充分必要条件，故不符合题意；

对于D，若，说明是实数，反之若是负实数，则不成立，符合题意．

故选：D．

点睛

本题考查了复数的分类，共轭复数和充分必要条件的判断，属于基础题．熟练掌握复数有关概念，是解决本题的关键．

4、答案D

解析由得，然后利用复数的除法和加法法则可求出复数.

详解

，，故选：D.

点睛

本题考查复数的计算，解题时充分利用复数的四则运算法则求出复数，也可以将所求复数设为一般形式，利用复数的四则运算法则和复数相等，列方程组求解，考查计算能力，属于基础题.

5、答案C

解析对于①中，根据复数的模的计算公式，即可判定是正确的；对于②中，根据复数的概念与分类，即可判定是正确的；对于③中，根据复数的运算与复数的概念，即可判定是正确；对于④中，根据复数的运算和复数相等的条件，即可判定不正确．

详解

由题意，对于①中，因为，根据复数的模的计算公式，可得，即，所以是正确的；

对于②中，若复数为实数，根据复数的概念，可得，反之，当时，复数为实数，所以是正确的；

对于③中，，若是纯虚数，则且，所以正确；

对于④中，由，即，所以，所以，所以不正确；

综上①②③为真命题，故选C．

点睛

本题主要考查了复数的基本概念，以及复数的运算，其中解答中熟记复数的基本概念和复数的分类，以及复数的运算法则是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题．

6、答案A

解析由题意可得：，

则，据此可得，的虚部为.故选：A.

7、答案C

解析，

所以的实部为，虚部为 ，

的共轭复数为，模为，

故选C.

8、答案B

解析根据复数对应复平面的点，然后判断对应三角函数的符号即可得到答案.

详解

解：因为为第二象限角．所以，即复数的实部为负数，虚部为正数，所以对应的点在第二象限．

故选：B．

点睛

本题主要考查复数对应的复平面的点的相关概念，难度较小.

9、答案B

详解：由，可得，

∴的虚部是4.

故选：B

点睛：本题考查复数的加减运算及虚部概念，属于基础题.

10、答案B

解析根据已知得复数z的表达式，再根据复数的除法运算，将复数z的分子、分母同时乘以分母的共轭复数，计算化简得复数z，从而得解.

详解

由得

，

所以复数z的实部为，

故选B.

点睛

本题考查复数的概念与乘法、除法运算，属于基础题.

11、答案D

解析运用复数除法的运算法则,化简复数,最后选出正确答案.

详解

因为,所以复平面内复数表示的点的坐标为,该点在第四象限.

故选：D

点睛

本题考查了复数除法的运算法则.考查了复数在复平面表示点的位置问题.

12、答案A

解析通过复数的四则运算，求出复数.

详解

因为，所以的虚部为2.

点睛

本题考查复数的四则运算及复数虚部的定义.

13、答案或

解析设出复数，化简，即可求解.

详解

设复数，则，所以则或，所以或.

故答案为：或

点睛

本题主要考查复数的模长，共轭复数，考查运算求解能力，属于基础题.

14、答案

解析因为，所以，

设，则，

故，，

联立，解得，，

则，

故答案为：.

15、答案0

解析先根据复数的除法计算出的结果，然后即可判断出的实部是多少.

详解

因为，所以.

故答案为：.

点睛

本题考查复数的除法运算以及复数的虚、实部辨别，难度较易.复数的除法运算时注意分母实数化.

16、答案

解析利用复数的乘除法计算可得答案.

详解

因为,

所以复数的实部为.

故答案为:.

点睛

本题考查了复数的乘除法运算以及复数的概念,属于基础题.

17、答案（1）；（2）

（2）由复平面上对应的点在直线上.，则复数对应点的坐标在直线上，代入直线方程求解即可.

详解：（1）因为复平面上对应的点在第二象限，

所以，

所以，

解得.

（2）因为在复平面上对应的点在直线上，

所以，

所以，

解得.

点睛

本题主要考查了复数的几何意义及对数方程和对数不等式的解法，还考查了运算求解的能力，属于中档题.

解析

18、答案，

详解：解：因为，，

所以，

因为是实数，

所以，即：

所以，，

所以，

点睛

本题考查复数的乘法运算，复数的相关概念，复数的模等知识，考查运算能力，是基础题.

解析

19、答案（1）；（2）.

（2）由图形求得，，代入，再由复数代数形式的乘除运算化简得答案.

详解：解：（1），

；

（2），，

.

点睛

本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题.

解析