2020-2021学年27.3 位似教案配套课件ppt

这是一份2020-2021学年27.3 位似教案配套课件ppt，共9页。PPT课件主要包含了－12，点D的横坐标为2，点B的横坐标为5，相似比为，－10等内容，欢迎下载使用。

在前面几册教科书中，我们学习了在平面直角坐标系中，如何用坐标表示某些平移、轴对称、旋转（中心对称）等变换，相似也是一种图形的变换，一些特殊的相似（如位似）也可以用图形坐标的变化来表示．
如图，在平面直角坐标系中，有两点A（6，3），B（6，0）．以原点O为位似中心，相似比为 ，把线段AB缩小，观察对应点之间坐标的变化，你有什么发现？
位似变换后A，B的对应点为A ' （ ， ），B'（ ， ）；A"（ ， ），B" （ ， ）．
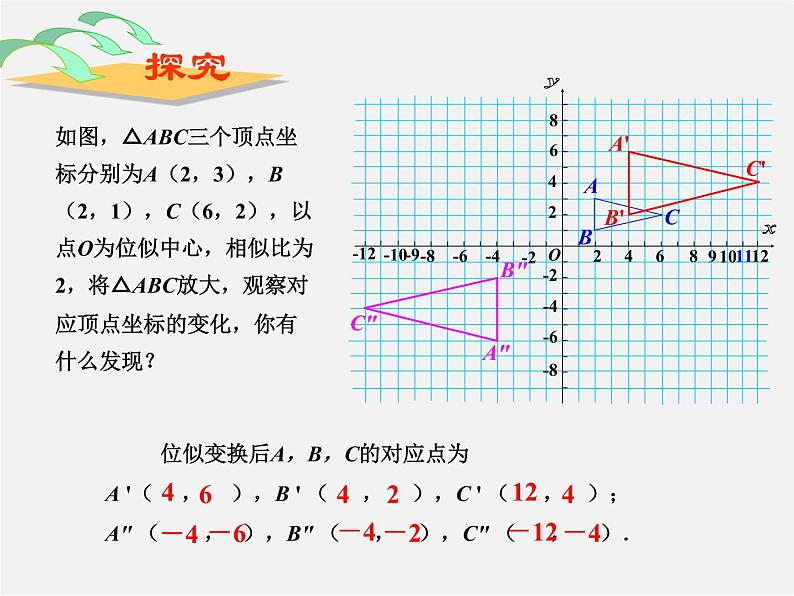
如图，△ABC三个顶点坐标分别为A（2，3），B（2，1），C（6，2），以点O为位似中心，相似比为2，将△ABC放大，观察对应顶点坐标的变化，你有什么发现？
位似变换后A，B，C的对应点为A '（ ， ），B ' （ ， ），C ' （ ， ）；A" （ ， ），B" （ ， ），C" （ ， ）．
在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或－k．
例 如图，四边形ABCD的坐标分别为A（－6，6），B（－8，2），C（－4，0），D（－2，4），画出它的一个以原点O为位似中心，相似比为 的位似图形．
分析：问题的关键是要确定位似图形各个顶点的坐标．根据前面的规律，点A的对应点A‘的坐标为 ，即（－3，3）．类似地，可以确定其他顶点的坐标．
解：如图，利用位似变换中对应点的坐标的变化规律．分别取点A'（ ， ），B ' （ ， ），C ' （ ， ），D'（ ， ）．
依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形．
练习1. 如图表示△AOB和把它缩小后得到的△COD，求它们的相似比．
2. 如图，△ABC三个顶点坐标分别为A（2，－2），B（4，－5），C（5，－2），以原点O为位似中心，将这个三角形放大为原来的2倍．
解：A'（ ， ），B ' （ ， ），C ' （ ， ），
A" （ ， ），B" （ ， ），C" （ ， ），