人教版九年级上册24.2.2 直线和圆的位置关系说课ppt课件

这是一份人教版九年级上册24.2.2 直线和圆的位置关系说课ppt课件，共17页。PPT课件主要包含了目标展示，切线长概念，动手发现折一折，切线长定理，例题解析等内容，欢迎下载使用。

1.理解切线长的概念，掌握切线长定理．2.学会运用切线长定理解决有关问题3．通过对例题的分析，培养学生分析总结问题的习惯，提高学生综合运用知识解题的能力，培养数形结合的思想．
经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长.
切线与切线长是一回事吗？它们有什么区别与联系呢？
切线与切线长的区别与联系：
（1）切线是一条与圆相切的直线；
（2）切线长是指切线上某一点与切点间的线段的长。
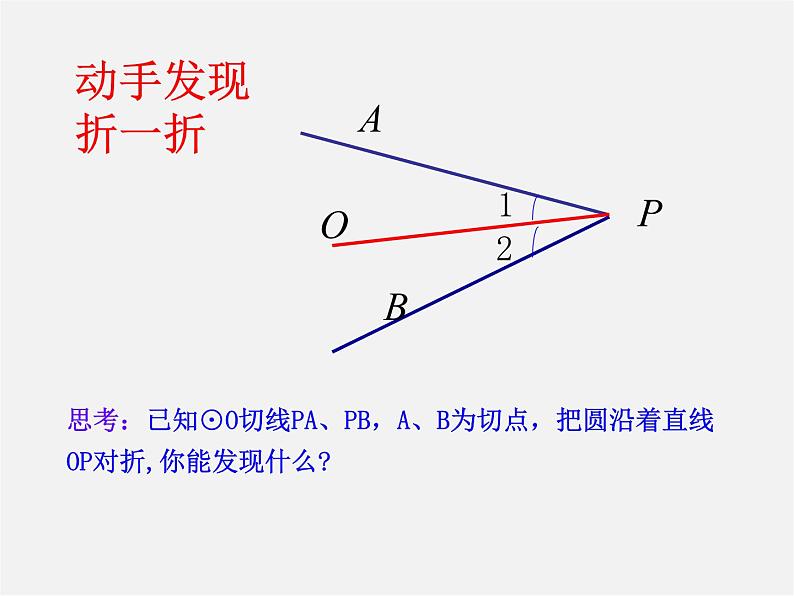
思考：已知⊙O切线PA、PB，A、B为切点，把圆沿着直线OP对折,你能发现什么?
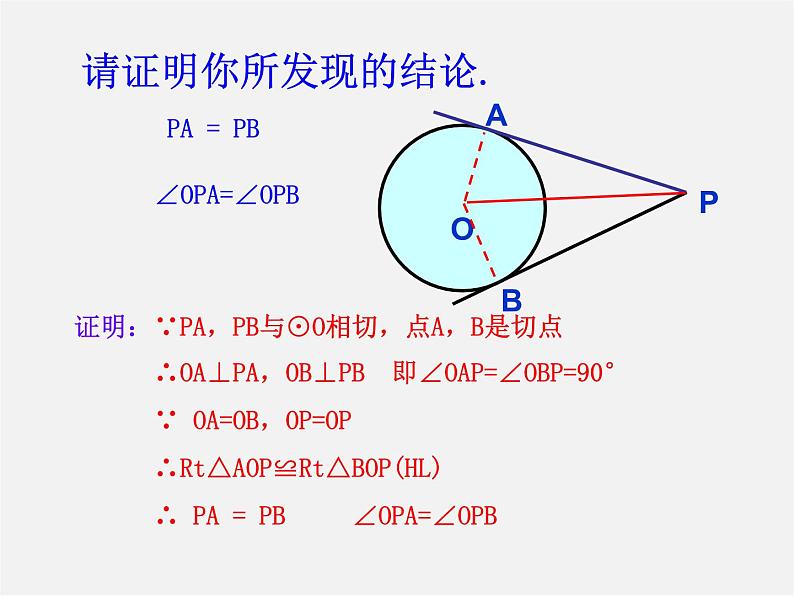
请证明你所发现的结论.
证明：∵PA，PB与⊙O相切，点A，B是切点 ∴OA⊥PA，OB⊥PB 即∠OAP=∠OBP=90° ∵ OA=OB，OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB ∠OPA=∠OPB
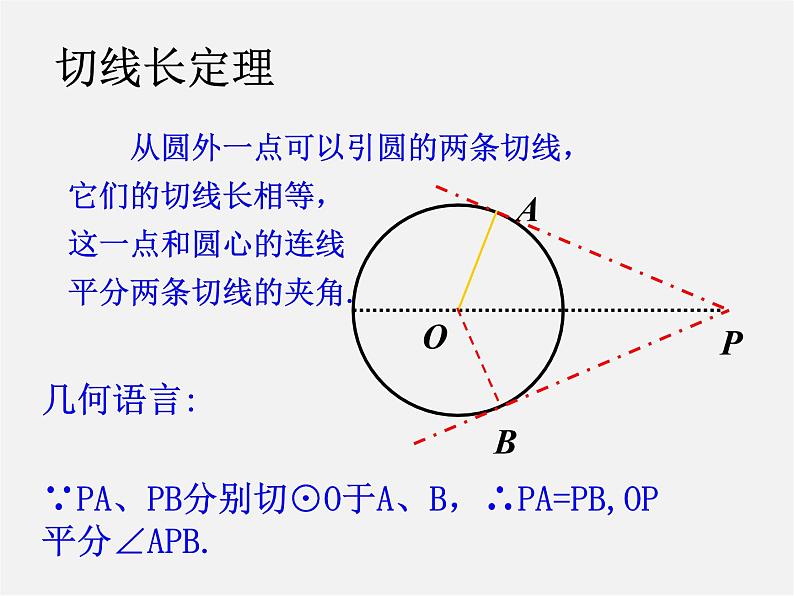
∵PA、PB分别切⊙O于A、B，∴PA=PB,OP平分∠APB.
从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.
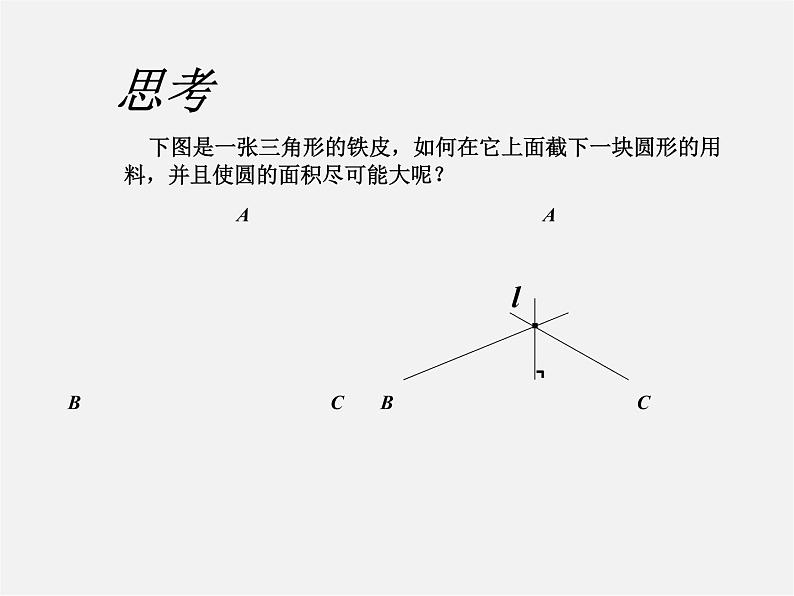
下图是一张三角形的铁皮，如何在它上面截下一块圆形的用料，并且使圆的面积尽可能大呢？
假设符合条件的圆已经作出，那么它应当与三角形的三条边都相切，这个圆的圆心到三角形三条边的距离都等于半径，如何找到这个圆的圆心呢？
三角形的三条角平分线交于一点，并且这个点到三条边的距离相等，因此，如图，分别作出∠B、∠C的平分线BM和CN，设他们相交于点I，那么点I到AB、BC、CA的距离都相等，以点I为圆心，点I到BC的距离ID为半径做圆，则⊙I与△ABC的三条边都相切.
内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.
与三角形各边都相切的圆叫做三角形的内切圆，
外接圆圆心：三角形三边垂直平分线的交点。外接圆的半径：交点到三角形任意一个顶点的距离。
内切圆圆心：三角形三个内角平分线的交点。内切圆的半径：交点到三角形任意一边的垂直距离。
【例2】△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=9cm，BC=14cm，CA=13cm，求AF、BD、CE的长.
设AF=x(cm),则AE=x(cm)
∴CD=CE=AC-AE=(13-x)cm BD=BF=AB-AF=(9-x)cm
由 BD+CD=BC可得 (13-x)+(9-x)=14
∴ AF=4(cm), BD=5(cm), CE=9(cm).
1.如图， △ABC中，∠ABC=50°∠ACB=75°，点O是内心，求∠BOC的读数.
2.△ABC的内切圆半径为r， △ABC的周长为l，求△ABC的面积.（提示：设内心为O，连接OA、OB、OC.）
解： 设: AB = a BC =b AC =c
3（杭州·中考）如图，正三角形的内切圆半径为1，那么这个正三角形的边长为（ ）A．2 B．3 C． D． 【解析】选D.如图所示，连接OA、OB，则三角形AOB是直角三角形，且∠OBA=90°,∠OAB=30°,又因为内切圆半径为1，利用勾股定理求得AB= 那么这个正三角形的边长为 .
4、如图，四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P，求证： AD+BC=AB+CD
证明：由切线长定理得AL=AP，LB=MB，NC=MC，DN=DP∴AL+LB+NC+DN=AP+MB+MC+DP即AB+CD=AD+BC补充：圆的外切四边形的两组对边的和相等．