人教版八年级下册18.2.1 矩形图片ppt课件

这是一份人教版八年级下册18.2.1 矩形图片ppt课件，共22页。PPT课件主要包含了从角上看，矩形的四个角都是直角，矩形的对角线相等，B对边相等，营中热身，营中寻宝等内容，欢迎下载使用。

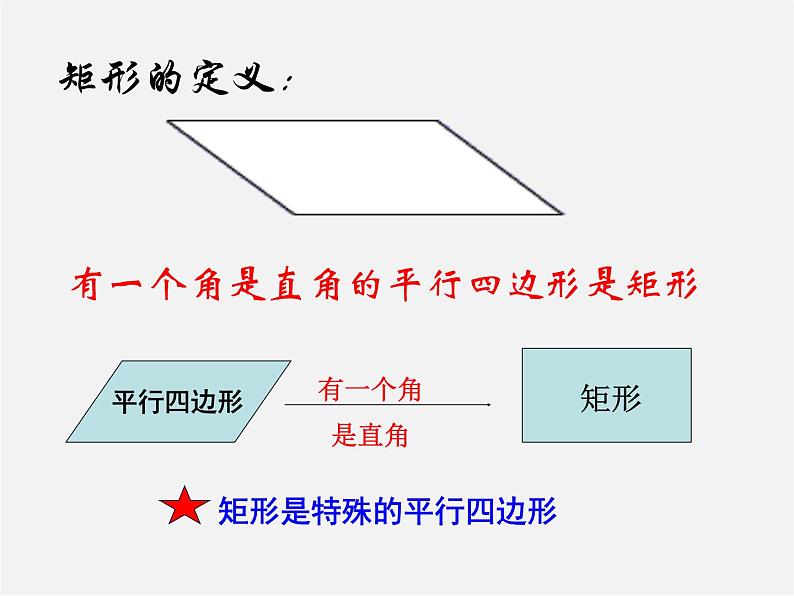
有一个角是直角的平行四边形是矩形
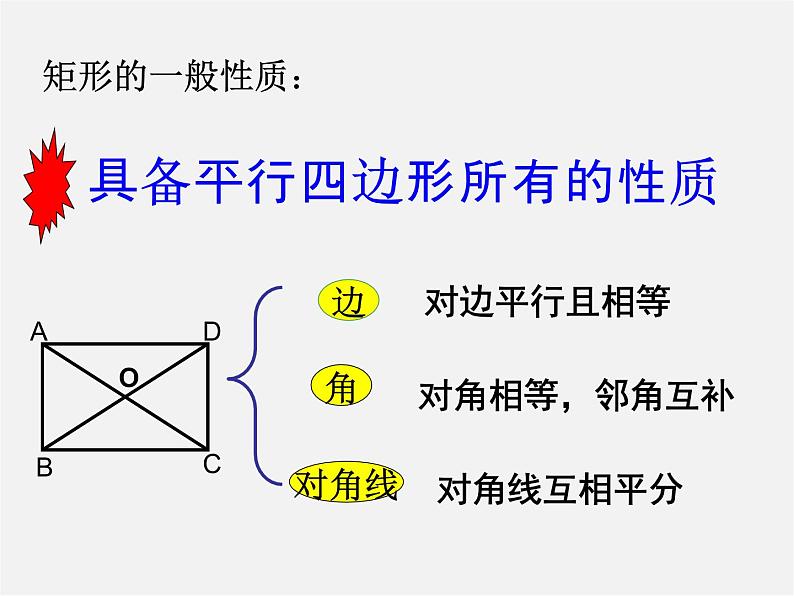
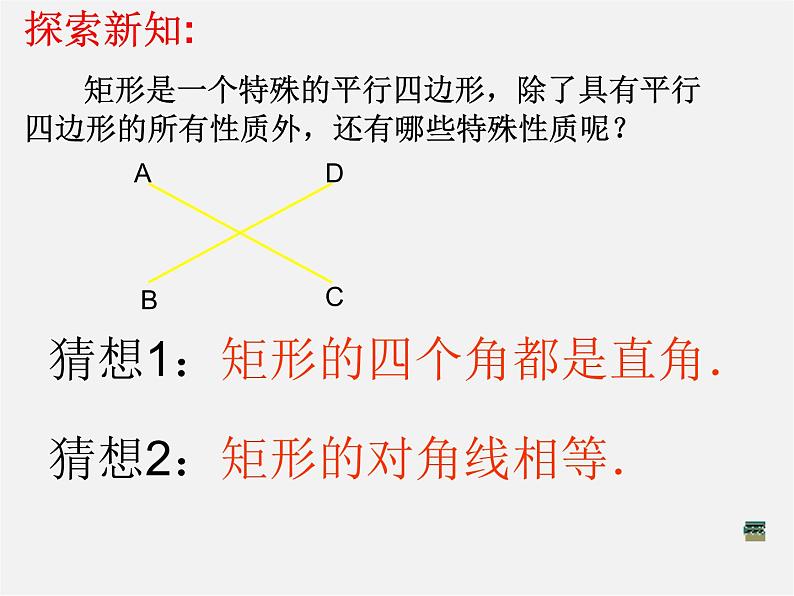
探索新知: 矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？
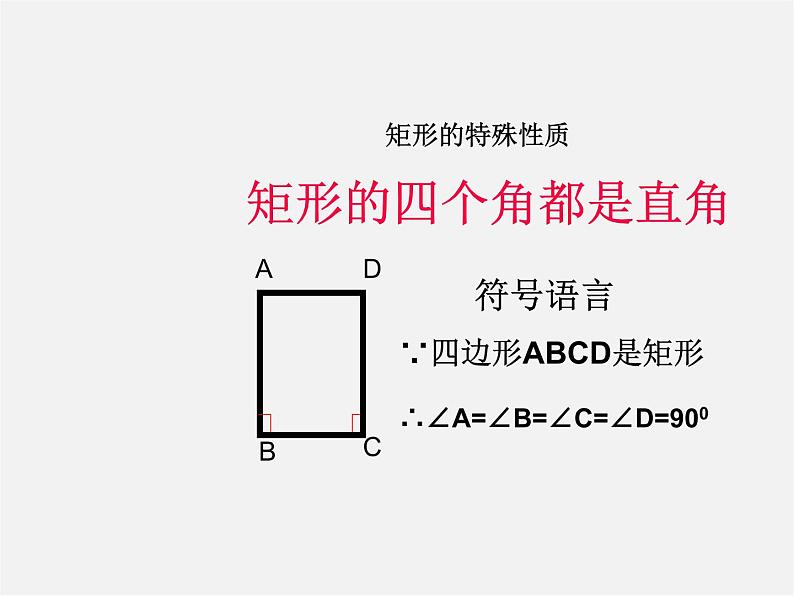
猜想1：矩形的四个角都是直角．
猜想2：矩形的对角线相等．
求证：矩形的四个角都是直角．
已知：如图，四边形ABCD是矩形
求证：∠A=∠B=∠C=∠D=90°
证明： ∵四边形ABCD是矩形
∵矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D 又∠A +∠B + ∠C + ∠D = 360°
∴ ∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
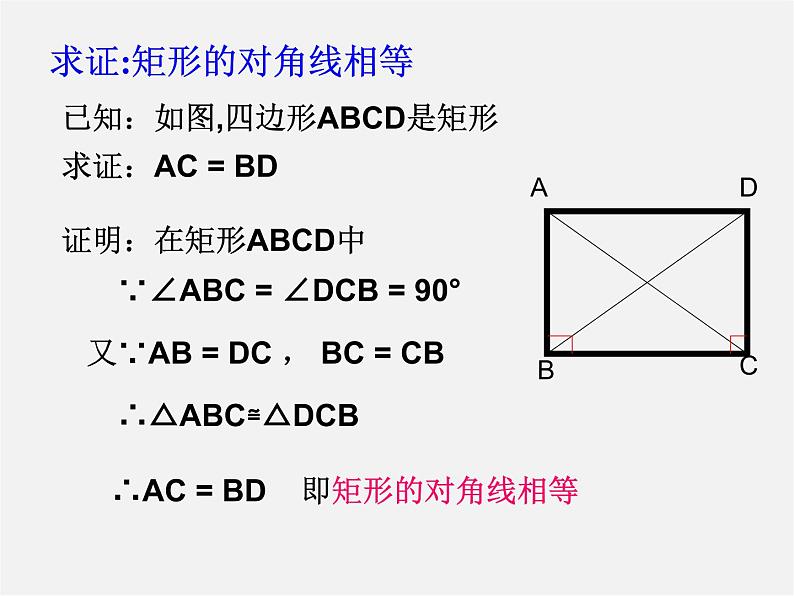
已知：如图,四边形ABCD是矩形 求证：AC = BD
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形的四个角都是直角．
矩形的两条对角线相等．
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
矩形的四个角都是直角；
矩形的对角线相等且互相平分；
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
得到：直角三角形的一个性质直角三角形斜边上的中线等于斜边的一半.
符号语言: ∵在Rt△ABC中, BO是斜边AC上的中线 ∴ BO= AC
在Rt△ABC中, BO= BD = AC
例: 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°,AB=4㎝,求矩形对角线的长？
方法小结: 如果矩形两对角 线的夹角是60° 或120°, 则其中必有等边三角形.
∴AC与BD相等且互相平分
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解：∵ 四边形ABCD是矩形
如图，在矩形ABCD中，找出相等的线段与相等的角。
　矩形具有而一般平行四边形不具有的性质是 ( )
已知:四边形ABCD是矩形1.若已知AB=8㎝，AD=6㎝， 则AC＝_______ ㎝ ，OB=_______ ㎝2.若已知 ∠DOC=120°，AC＝8㎝，则AD= _____cm，AB= _____cm
4.已知△ABC是Rt△，∠ABC=900，BD是斜边AC上的中线
(1)若BD=3㎝，则AC＝ ㎝(2) 若∠C=30°，AB＝5㎝，则AC＝ ㎝， BD＝ ㎝.
矩形的四个角都是直角.
※ 矩形的性质定理1
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
1、工人师傅做铝合金窗框分下面三个步骤进行：（1）先截出两对符合规格的铝合金窗料（如图1），使AB=CD, EF=GH;（2）摆放成如图（2）的四边形，则这时窗框的形状是＿＿＿，根据的数学道理是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；（3）将直角尺靠紧窗框的一个角（如图3）调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图4），说明窗框合格，这时窗框是＿＿＿＿，根据的数学道理是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
两组对边分别相等的四边形是平行四边形
　3. 过四边形的各个顶点分别作对角线的平行线，若这四条平行线围成一个矩形，则原四边形一定是
2. 下面性质中，矩形不一定具有的是
　A．对角线相等 B．四个角都相等 C．是轴对称图形 D．对角线垂直
A．对角线相等的四边形 B．对角线互相平分且相等的四边形C．对角线互垂直平分的四边形 D．对角线垂直的四边形
[ ]
　A．50° B．60° C．70° D．80°
5. 矩形ABCD中，AB=2BC，E在CD上，AE=AB，则∠BAE等于
　A．30° B．45° C．60° D．120°
4. 已知矩形的一条对角线与一边的夹角是40°，则两条对角线所夹锐角的度数为