初中数学人教版八年级上册12.2 三角形全等的判定示范课课件ppt

这是一份初中数学人教版八年级上册12.2 三角形全等的判定示范课课件ppt，共24页。PPT课件主要包含了注重书写格式，2三条边，1三个角，3两边一角，4两角一边，SSS，探索边角边，练习一，探索边边角，SSSSAS等内容，欢迎下载使用。

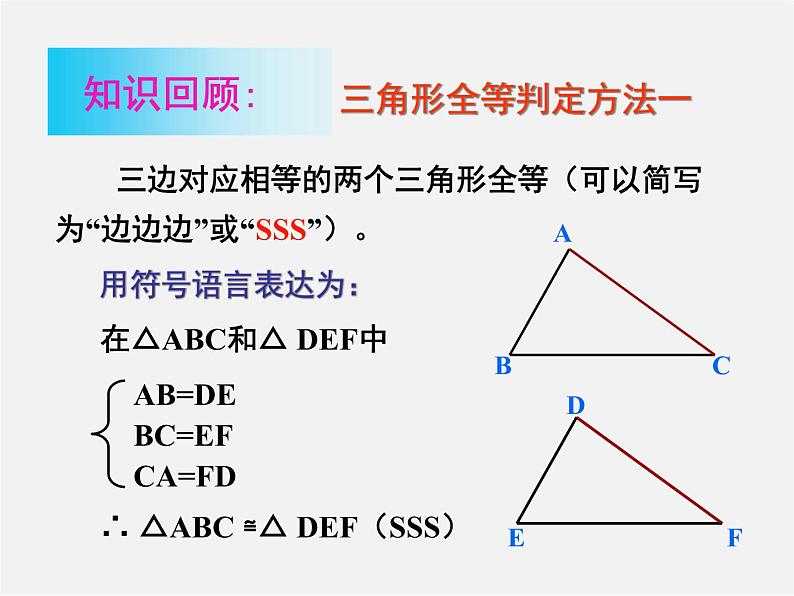
三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）。
在△ABC和△ DEF中
∴ △ABC ≌△ DEF（SSS）
三角形全等判定方法一
除了SSS外，还有其他情况吗？继续探索三角形全等的条件。
当两个三角形满足六个条件中的三个时，有四种情况:
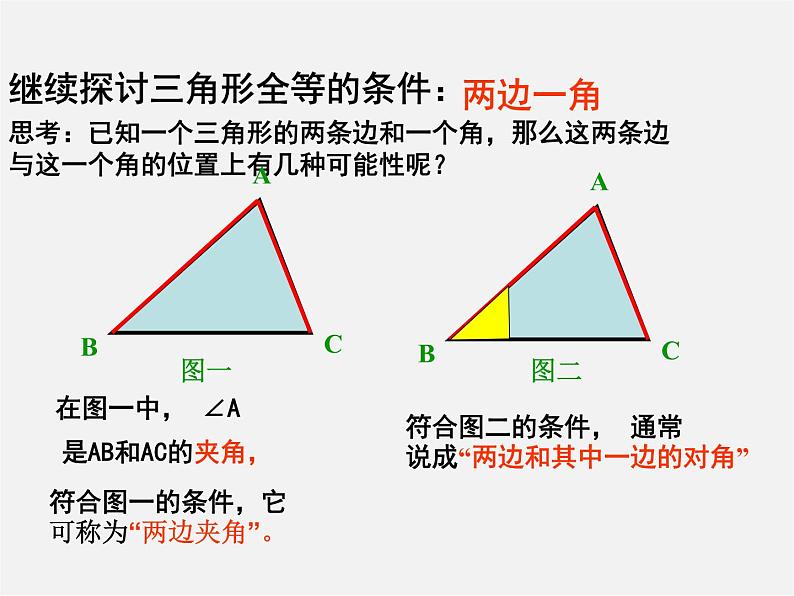
继续探讨三角形全等的条件：
思考：已知一个三角形的两条边和一个角，那么这两条边与这一个角的位置上有几种可能性呢？
符合图一的条件，它可称为“两边夹角”。
符合图二的条件， 通常说成“两边和其中一边的对角”
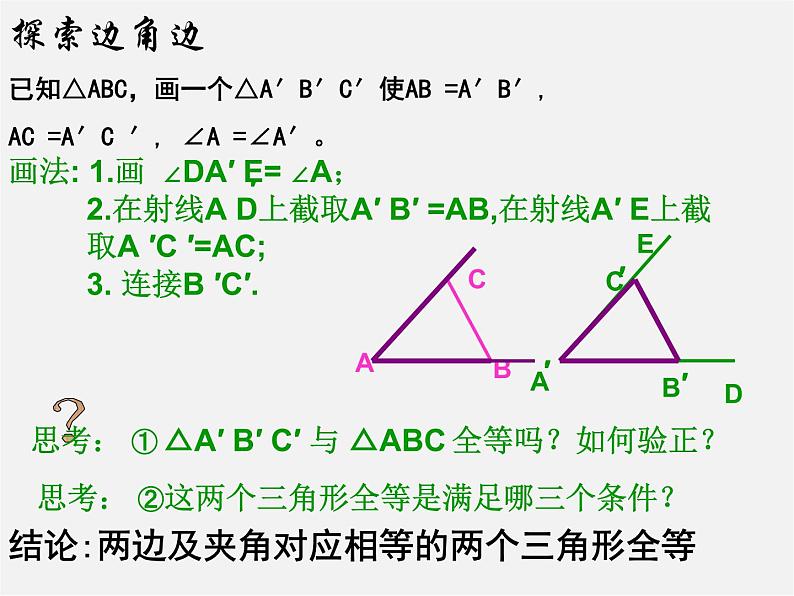
已知△ABC，画一个△A′B′C′使AB =A′B′,AC =A′C ′, ∠A =∠A′。
结论:两边及夹角对应相等的两个三角形全等
思考： ① △A′ B′ C′ 与 △ABC 全等吗？如何验正？
画法: 1.画 ∠DA′ E= ∠A；
2.在射线A D上截取A′ B′ =AB,在射线A′ E上截取A ′C ′=AC;
3. 连接B ′C′.
思考： ②这两个三角形全等是满足哪三个条件？
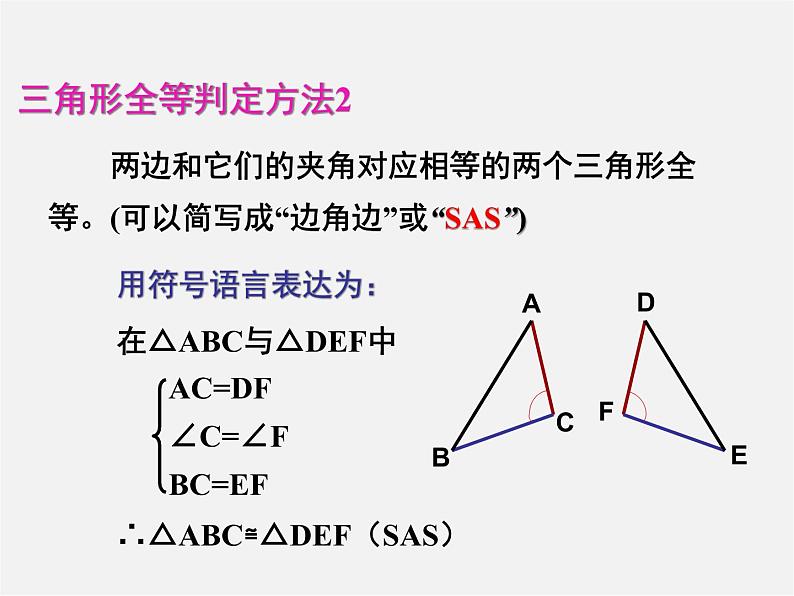
三角形全等判定方法2
在△ABC与△DEF中
∴△ABC≌△DEF（SAS）
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
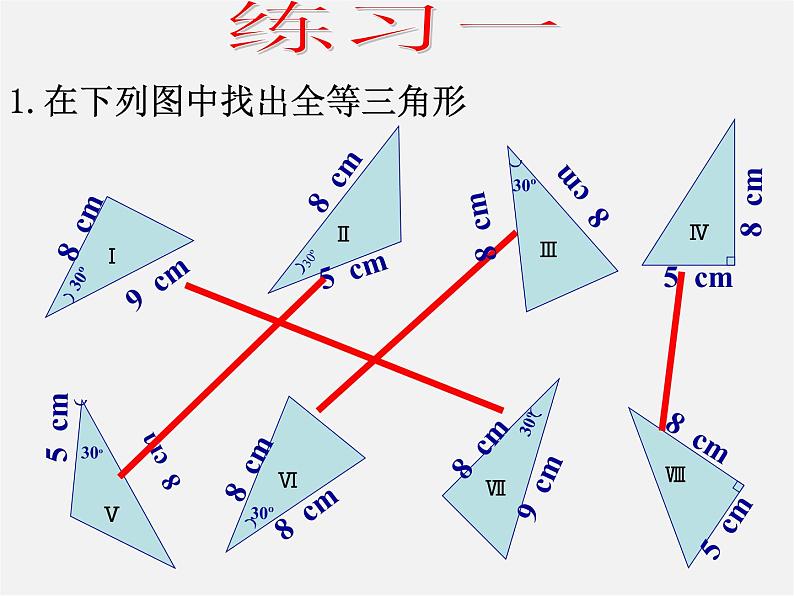
1.在下列图中找出全等三角形
两边及其中一边的对角对应相等的两个三角形全等吗?
已知：AC=5cm,BC=3cm, ∠A=45 °.
△ABC的形状与大小是唯一确定的吗?
显然： △ABC与△AB’C不全等
两边及一角对应相等的两个三角形全等吗？
①两边及夹角对应相等的两个三角形全等（SAS)；
②两边及其中一边的的对角对应相等的两个三角形不一定全等．
③ 现在你知道哪些三角形全等的判定方法？
　　例2　如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个不经过池塘可以直接到达点A 和B的点C，连接AC并延长至D，使CD =CA，连接BC 并延长至E，使CE =CB，连接ED，那么量出DE的长就是A，B的距离．为什么？
证明：在△ABC 和△DEC 中，
∴　△ABC ≌△DEC（SAS）．∴　AB =DE （全等三角形的对应边相等）．
如图，AC=BD，∠CAB= ∠DBA，你能判断BC=AD吗？说明理由。
证明:在△ABC与△BAD中
AC=BD ∠CAB=∠DBA AB=BA
∴△ABC≌△BAD（SAS）
∴BC=AD (全等三角形的对应边相等）
因为全等三角形的对应角相等，对应边相等，所以，证明分别属于两个三角形的线段相等或角相等的问题，常常通过证明两个三角形全等来解决。
在下列推理中填写需要补充的条件，使结论成立：(1)如图,在△AOB和△DOC中
AO=DO(已知)______=________( )BO=CO(已知)∴ △AOB≌△DOC（ ）
(2).如图，在△AEC和△ADB中，已知AE=AD，AC=AB，请说明△AEC ≌ △ADB的理由。
____=____(已知)∠A= ∠A( 公共角)_____=____(已知)∴ △AEC≌△ADB（ ）
解：在△AEC和△ADB中
1.若AB=AC，则添加什么条件可得△ABD≌ △ACD?
2.如图，要证△ACB≌ △ADB ，至少选用哪些条件可
证得△ACB≌ △ADB
∠CAB= ∠ DAB
1.边角边公理：有两边和它们的______对应相等的 两个三角形全等（SAS）
2.边角边公理的发现过程所用到的数学方法（包括画 图、实验、猜想、分析、归纳等.)
3.边角边公理的应用中所用到的数学方法: 证明线段（或角相等） 证明线段（或角）所在的两个三角形全等.
公理中所出现的边与角必须在所证明的两个三角形中. 公理中涉及的角必须是两边的夹角.要充分利用图形中的隐含条件，如公共边、公共角、对顶角等.
用公理证明两个三角形全等需注意
教科书第43页习题12.2第2题、第10题．
1．已知：如图，AB＝AC，F、E分别是AB、AC的中点． 求证：△ABE≌△ACF．2．已知：点A、F、E、C在同一条直线上， AF＝CE， BE∥DF，BE＝DF．求证：△ABE≌△CDF．
3.如图:己知AD∥BC,AE=CF,AD=BC,E、Ｆ都在直线ＡＣ上，试说明ＤＥ∥ＢＦ。