初中人教版16.2 二次根式的乘除备课ppt课件

第十六章　二次根式

16.2   二根次式的乘除

第2课时   二次根式的除法

一、 教学目标

理解＝(a≥0，b＞0)和＝(a≥0，b＞0)，会利用它们进行计算和化简．

二、 重点难点

重点

理解并掌握＝(a≥0，b＞0)，＝(a≥0，b＞0)，利用它们进行计算和化简．

难点

归纳二次根式的除法法则．

三、 教学设计

（一）   新知导入

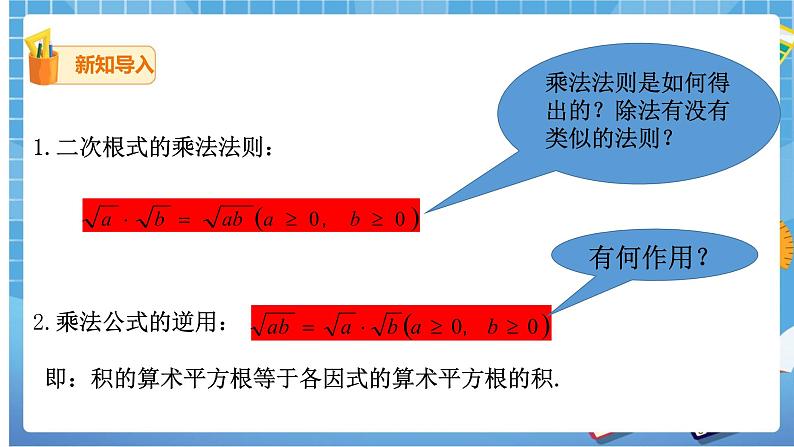
1. 二次根式的乘法法则?乘法法则是如何得出的？除法有没有类似的法则？
2. 乘法公式的逆用公式是什么？有何作用？

（二）   新知讲解

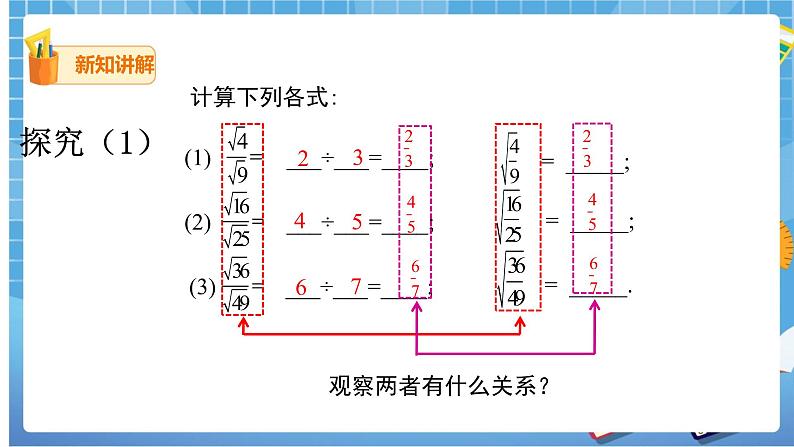
（三）   探究（1）

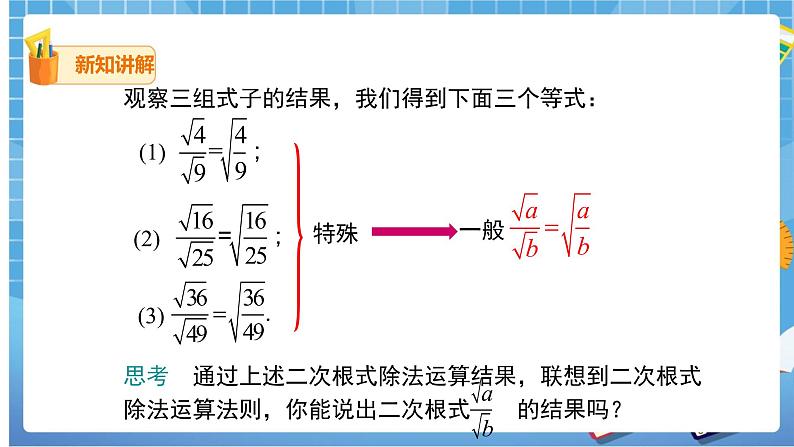
观察两者有什么关系？   

思考  通过上述二次根式除法运算结果，联想到二次根式除法运算法则，你能说出二次根式的结果吗？

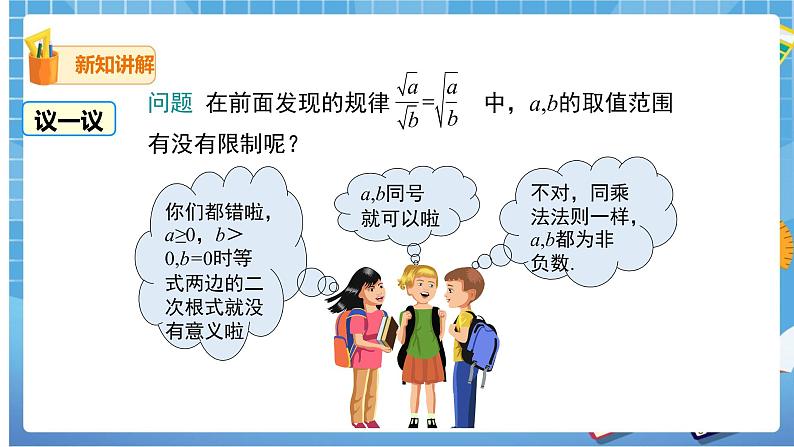
问题  在前面发现的规律中，a,b的取值范围有没有限制呢？

归纳总结

二次根式的除法法则:

文字叙述:

算术平方根的商等于被开方数商的算术平方根.

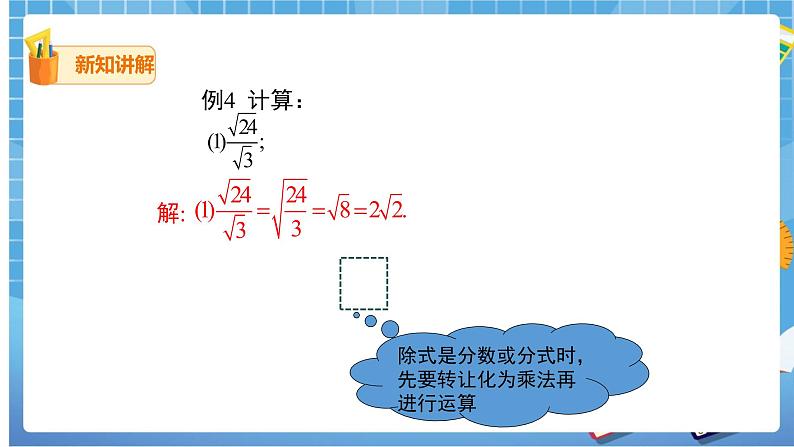
例4  计算：

我们知道，把二次根式的乘法法则反过来就得到积的算术平方根的性质.

类似的，把二次根式的除法法则反过来，就得到

二次根式的商的算术平方根的性质:

语言表述：商的算术平方根，等于积中各因式的算术平方根的商.我们可以运用它来进行二次根式的解题和化简.

例5  化简:

例6   计算:

归纳总结

   把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.

满足如下两个特点：

（1）被开方数不含分母；

（2）被开方数中不含能开得尽方的因数或因式.

我们把满足上述两个条件的二次根式，叫做最简二次根式.

简记为：一根号无分母，分母无根号；二不能再开方.

在二次根式的运算中，一般要把最后结果化为最简二次根式，并且分母中不含二次根式.

例7   设长方形的面积为S,相邻两边长分别为a,b.已知   ，求a的值.

例8 如果两个电视塔的高分别是h1km，h2km，那么它们的传播半径之比是试化简该式.

（四）   课堂练习(PPT14)(PPT15)

1.化简的结果是（　　）

A．9          B．3          C．          D．

2.下列根式中，最简二次根式是（　　）

 A.      B.         C.       D.

3.设长方形的面积为S,相邻两边长分别为a,b.已知  ，求a的值.

（五）   拓展提高(PPT16、PPT17)

. 1. 化简：

2.自习课上，张玉看见同桌刘敏在练习本上写的题目是“求二次根式中实数a的取值范围”，她告诉刘敏说：你把题目抄错了，不是“ ”，而是“”刘敏说：哎呀，真抄错了，好在不影响结果，反正a和a-3都在根号内．试问：刘敏说得对吗？

四、 课堂总结(PPT18)

一、本节课的主要内容是什么？

二、运用二次根式的除法法则的关键问题是什么？

三、学习最简二次根式有何意义？

四、本节课涉及的思想方法有哪些？

五、 板书设计

六、作业设计

　　课后作业：习题16.2 第2题、第3题、第4题