初中人教版17.1 勾股定理多媒体教学课件ppt

第十七章　勾股定理

17.1　勾股定理

第1课时　勾股定理

一、 教学目标

了解勾股定理的发现过程，理解并掌握勾股定理的内容，会用面积法证明勾股定理，能应用勾股定理进行简单的计算．

二、 重点难点

重点

勾股定理的内容和证明及简单应用．

难点

勾股定理的证明．

三、 教学设计

（一）   新知导入

展示PPT2、PPT3、PPT4

国际数学家大会是最高水平的全球性数学科学学术会议．2002年在北京召开了第24届国际数学家大会．如图就是大会的会徽的图案．

你见过这个图案吗？ 它由哪些基本图形组成？

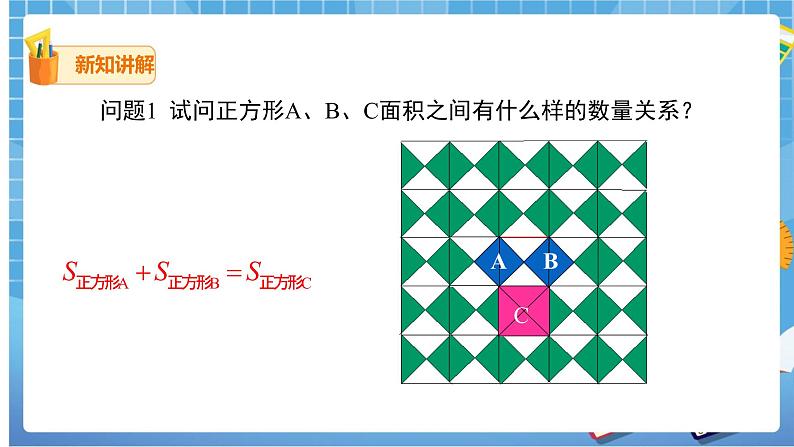
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。相传有一次他在朋友家做客时，发现朋友家用砖铺成的地面中反映了A、B、C三者面积之间的数量关系，进而发现直角三角形三边的某种数量关系．

（二）   新知讲解

问题1  试问正方形A、B、C面积之间有什么样的数量关系？

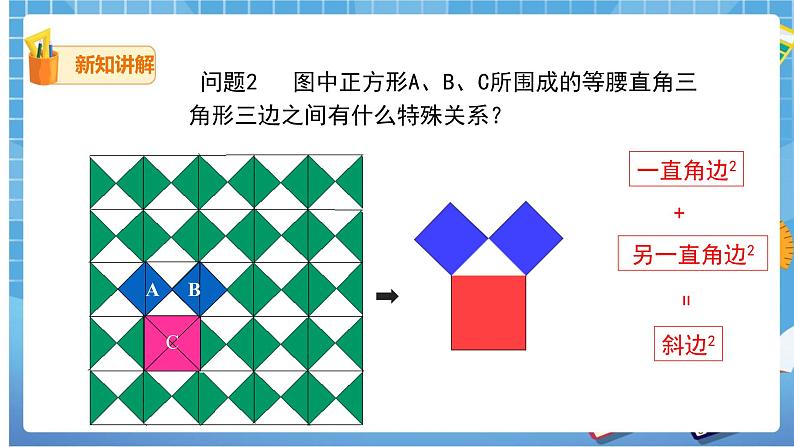
问题2   图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系？

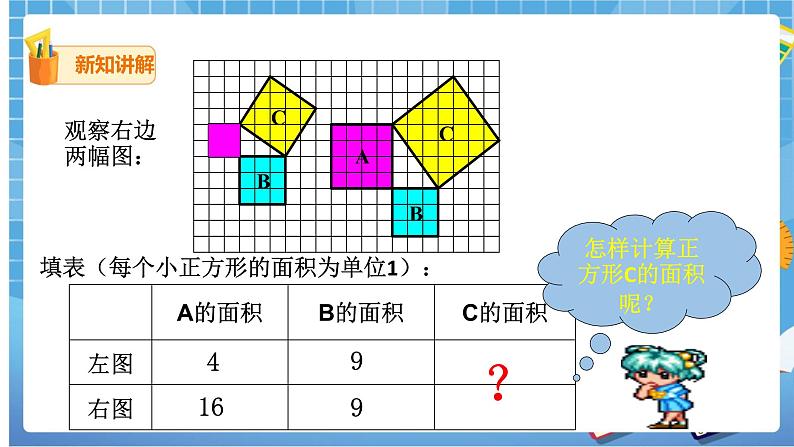
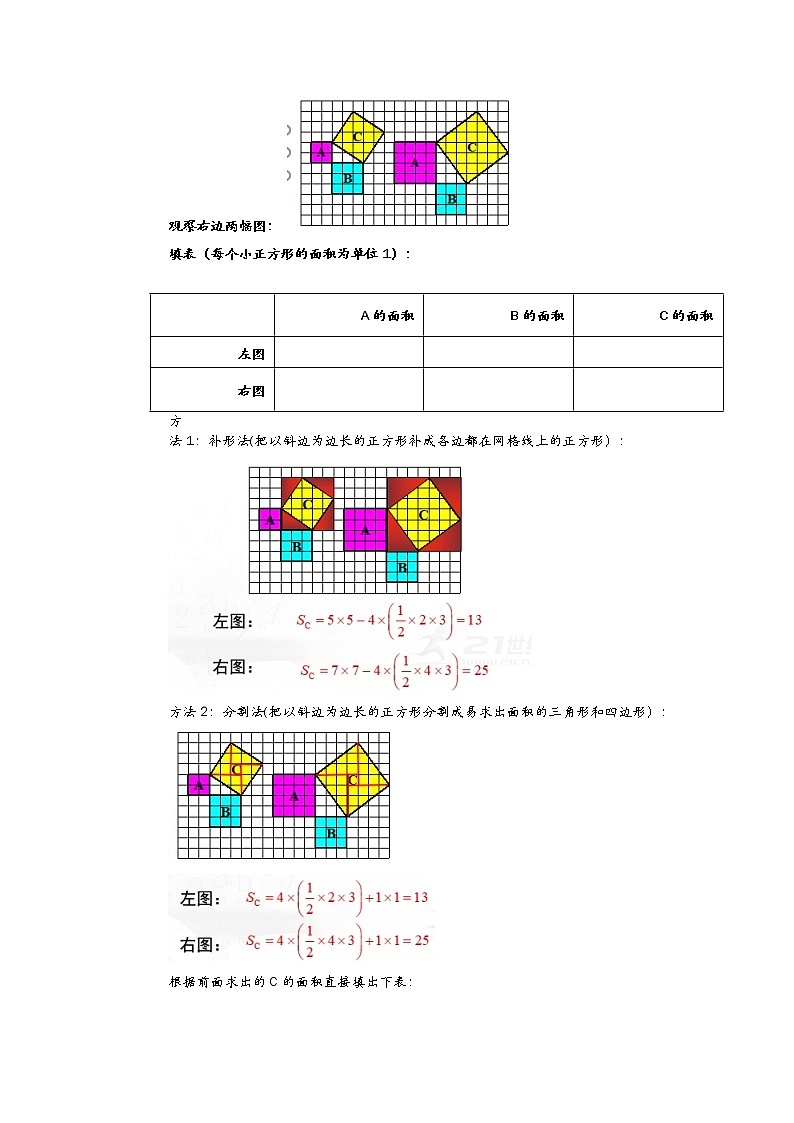
观察右边两幅图：

填表（每个小正方形的面积为单位1）：

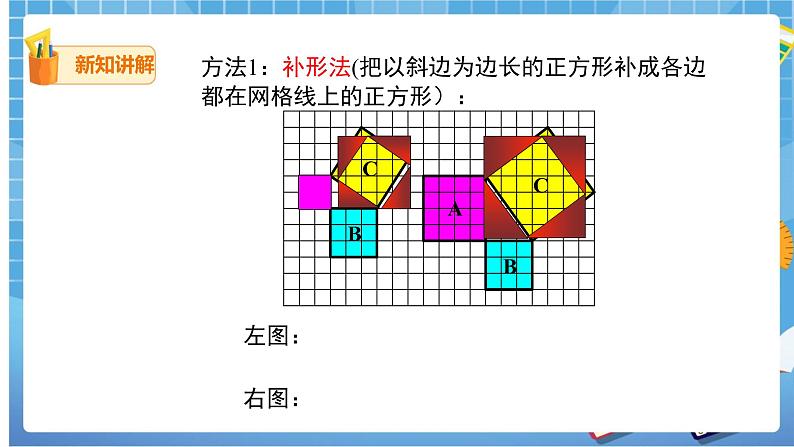
方法1：补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形）：

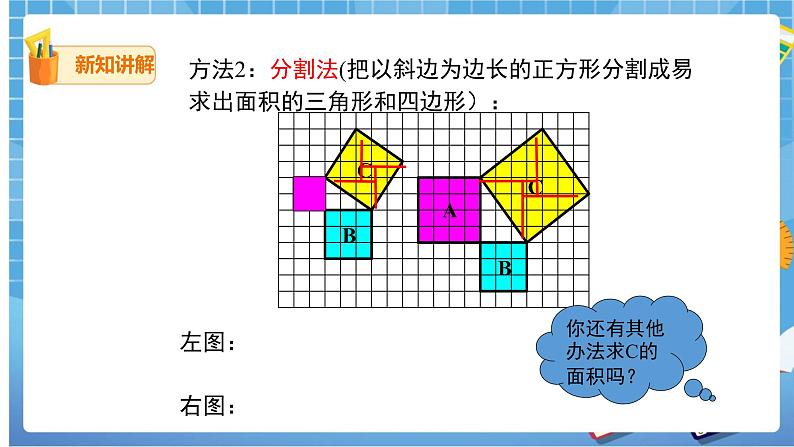
方法2：分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形）：

根据前面求出的C的面积直接填出下表：

思考   正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？

由上面的几个例子，我们猜想：

命题1   如果直角三角形的两条直角边长分别为a,b，斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.

下面动图形象的说明命题1的正确性，让我们跟着以前的数学家们用拼图法来证明这一猜想.

证明命题1的方法有很多，下面介绍我国古人赵爽的证法。

证法2  毕达哥拉斯证法

证法3    美国第二十任总统伽菲尔德的“总统证法”.

归纳总结

   如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.

在我国又称商高定理，在外国则叫毕达哥拉斯定理，或百牛定理.

我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”，我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.因此就把这一定理称为勾股定理.

     公式变形：

a、b、c为正数

（三）   课堂练习

1.下列说法中,正确的是                      （          ）

A.已知a,b,c是三角形的三边，则a2+b2=c2

B.在直角三角形中两边和的平方等于第三边的平方

C.在Rt△ABC中，∠C=90°,所以a2+b2=c2

D.在Rt△ABC中，∠B=90°,所以a2+b2=c2

2.图中阴影部分是一个正方形，则此正方形的面积为             .

3.　如图，所有的三角形都是直角三角形，四边形都是正方形，已知正方形A，B，C，D 的边长分别是12，16，9，12．求最大正方形E 的面积．

解：如图所示,正方形A、B、C、D的边长分别是12,16,9,12.

设直角三角形的斜边长为c .由勾股定理知,

122+162=c2,c=20 ，即正方形F的边长为20.

同理可得， 正方形G的边长为15.

故直角三角形的两直角边分别为20，15.

设它的斜边长为k，由勾股定理知,

202+152=k2，k=25.

 正方形E的边长为25，S正方形E=25×25=625

（四）   拓展提高

1.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.

解：设另一条直角边长是x cm.

 由勾股定理得152+ x2 =172，

 即x2=172-152=289–225=64，

∴ x=±8（负值舍去），

∴另一直角边长为8 cm，

直角三角形的面积是                    

四、 课堂总结

勾股定理：

在Rt△ABC中， ∠C=90°,a,b为直角边，c为斜边，则有a²+b²=c².

公式变形：

注意：1、在直角三角形中

2、看清哪个角是直角

3、已知两边没有指明是直角边还是斜边时一定要分类讨论

五、 板书设计

六、作业设计

　　　课后作业：课本第24页练习第1题，课本28页习题17.1第1题。