数学八年级上册15.2 线段的垂直平分线教学ppt课件

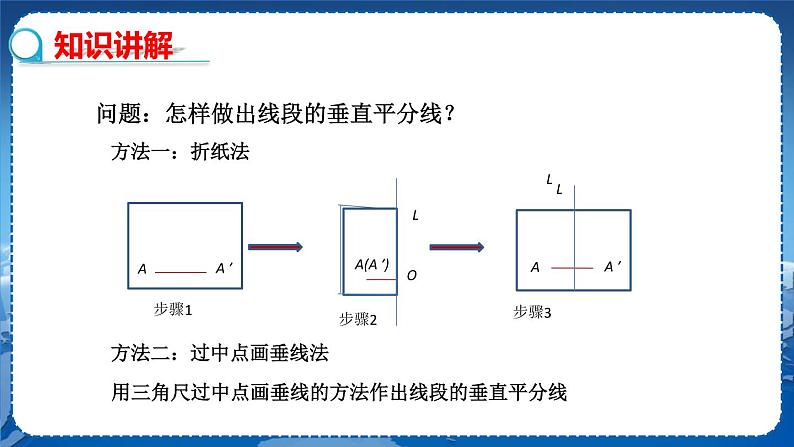
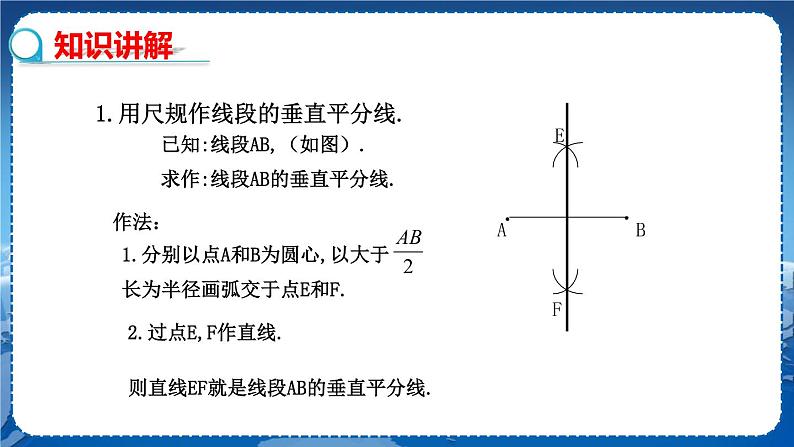
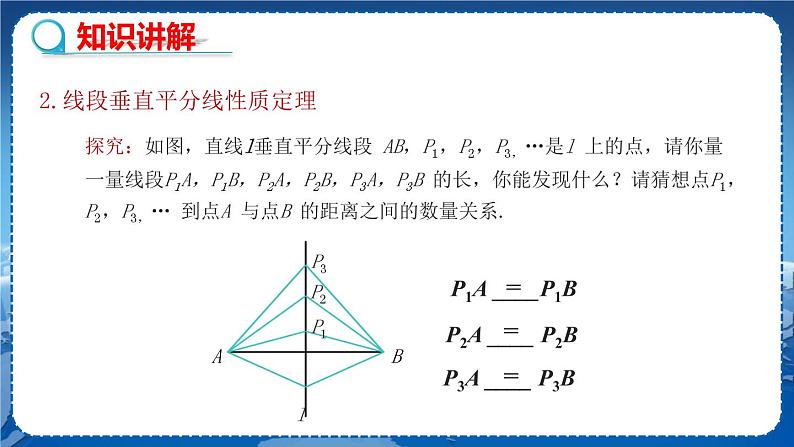
教学目标

1.能够利用尺规法作一条已知线段的垂直平分线，并能证明它的正确性.

2.经历探索、证明线段垂直平分线的性质定理及其逆定理的过程，进一步发展学生的推理证明意识和能力.

3.能够利用线段的垂直平分线的性质及其逆定理证明相关结论，理解三角形三边的垂直平分线相交于一点，这点到三角形三个顶点的距离相等.

教学重难点

重点：线段垂直平分线的有关性质.

难点：用尺规作图作线段的垂直平分线，并利用垂直平分线的性质解决一些实际问题.

教学过程

知识回顾

1.线段的垂直平分线的定义

经过线段的中点并且垂直于这条线段的直线叫作这条线段的垂直平分线.

2.如果两个图形关于某条直线对称，那么对称轴是任意一对对应点所连线段的垂直平分线，反过来，成轴对称的两个图形中，对应点的连线被对称轴垂直平分.

3.我们学过的作一条线段的垂直平分线方法：折纸法、过线段中点画垂线法

新课导入

某区政府为了方便居民的生活，计划在三个住宅小区 A、B、C 之间修建一个购物中心，试问该购物中心应建于何处，才能使得它到三个小区的距离相等？

探究新知

问题：怎样作出线段的垂直平分线？

【教师活动】在纸上画一条线段，将其标为AA′，然后将其对折，使A ，A′两点重合.接下来将纸展开.将折痕用笔画出，并将其与线段A A′的交点标为O，你能发现什么？AO与A′O是什么样的关系呢？

【学生活动】线段是轴对称图形，折痕所在的这条直线就是线段AB的对称轴，对折之后呢，AO与A′O是重合的，所以AO＝ A′O.

【教师提问】怎么利用尺规作线段AB的垂直平分线？

【学生活动】先独立思考，再与同伴交流.

已知：线段AB.

求作：AB的垂直平分线.

作法：

1.分别以点A和B为圆心，以大于AB一半的长为半径作弧，两弧相交于点E和F.

2.作直线EF.

直线EF就是线段AB的垂直平分线.

2.线段垂直平分线性质定理

【教师活动】出示探究问题，让学生动手测量，引导学生分析问题..

探究：如图，直线l垂直平分线段 AB，P1，P2，P3…是l 上的点，请你量一量线段P1A，P1B，P2A，P2B，P3A，P3B 的长，你能发现什么？请猜想点P1，P2，P3，… 到点A与点B 的距离之间的数量关系.

（1）P1A ____P1B；

（2）P2A ____ P2B；

（3）P3A ____ P3B.

【学生活动】动手测量线段，交流测量的结果，猜想存在的结论.

猜想：

点P1，P2，P3… 到点 A 与点 B 的距离分别相等. 

【教师活动】根据测量的结果，进行交流，由此你能得到什么结论？

【学生】用语言叙述得出的结论.

命题：线段垂直平分线上的点到线段两端的距离相等.

【教师活动】你能验证这一结论吗？（巡视学生做题情况，对出现的问题及时纠正）

【学生活动】按照题意画出图形，写出已知，求证，写出证明过程，在小组内交流.

验证：

已知：如图，直线MN经过线段AB的中点，且MN⊥AB，垂足为O，P 是MN上任意一点.

求证：PA ＝PB.

证明：∵ MN⊥AB，(已知)

∴ ∠AOP ＝∠BOP＝90°（垂直定义）.

在△AOP和△BOP中，

∵ 

∴ △AOP ≌△BOP（SAS）.

∴ PA＝PB（全等三角形对应边相等）.

【师生互动总结】文字叙述线段垂直平分线的性质定理，并用几何语言进行叙述.

结论：

线段垂直平分线的性质定理：

线段垂直平分线上的点到这条线段两端的距离相等.

几何语言：

∵ 　CO是线段AB的垂直平分线，

∴ 　AC＝BC.

典型例题

例1　如图，在△ABC 中，AB＝AC＝20 cm，DE 垂直平分AB，垂足为E，交AC于D，若△DBC 的周长为35 cm，则BC 的长为（     ）

A.5 cm    B.10 cm    C.15 cm    D.17.5 cm

解析： ∵  △DBC 的周长为BC＋BD＋CD＝35 cm，

又∵  DE 垂直平分AB，

∴  AD＝BD，故BC＋AD＋CD＝35 cm.

∵  AC＝AD＋DC＝20 cm，

∴  BC＝35－20＝15(cm).

答案：C

【互动总结】利用线段垂直平分线的性质，实现线段之间的相互转化，从而求出未知线段的长.

3.线段垂直平分线的判定

探究

想一想：如果 PA＝PB ,那么点 P 是否在线段 AB 的垂直平分线上呢？

已知：如图，PA ＝PB.

求证：点P 在线段 AB 的垂直平分线上.

性质定理：线段垂直平分线上的点到线段两端的距离相等.

你能写出这个定理的逆命题吗？

如果有一个点到线段两个端点的距离相等，那么这个点在这条线段的垂直平分线上，即到线段两端点的距离相等的点在线段的垂直平分线上.

当我们写出逆命题时，就想到判断它的真假.如果真，则需证明它；如果假，则需用反例说明.

性质定理的逆命题：

到线段两端距离相等的点在线段的垂直平分线上.

【教师活动】提出探究问题，让学生写出线段垂直平分线性质定理的逆命题，指导学生根据逆命题写出已知和求证，分析证明思路，巡视学生做题情况，并及时点拨.

【学生活动】先小组交流线段垂直平分线性质定理的逆命题，写出命题的已知和求证，分析证明方法，由两名学生分别到黑板板演证明过程，小组内交流证明过程.

已知：线段AB，点P是平面内一点且PA＝PB.

求证：P点在AB的垂直平分线上.

证明：（方法一）

过点P 作AB 的垂线PC，垂足为点C.

则∠PCA ＝∠PCB ＝90°.

在Rt△PCA 和Rt△PCB中，

  PA＝PB，PC＝PC，

∴  Rt△PCA ≌Rt△PCB（HL）.

∴   AC＝BC.

又PC⊥AB，

∴ 点P 在线段AB的垂直平分线上.

（方法二）把线段AB的中点记为O,连接PO.

   ∵ O为AB的中点，

   ∴ AO＝BO.

   ∵ PA＝PB,PO＝PO，

   ∴ △APO ≌△BPO（SSS），

   ∴ ∠POA＝∠POB＝90°，

   ∴ PO⊥AB， 即P在AB的垂直平分线上.

【师生互动总结】根据证明的结论，师生总结线段垂直平分线的判定，并用几何语言进行描述，总结定理的作用.

结论：

线段垂直平分线的判定：

到线段两端距离相等的点在线段的垂直平分线上.

应用格式：

∵  PA＝PB，

∴  点P在AB 的垂直平分线上.

作用：

判断一个点是否在线段的垂直平分线上.

典型例题

例2  已知：如图, △ABC 的边AB，BC 的垂直平分线交于P.

 求证：点P在线段AC的垂直平分线上.

证明：连接PA，PB，PC.

∵ 点P在线段AB，BC的垂直平分线上，(已知)

∴ PA＝PB，PB＝PC.(线段垂直平分线上的点到线段两端的距离相等)

∴ PA＝PC（等量代换）

∴ 点P在AC的垂直平分线上（到线段两端距离相等的点在线段的垂直平分线上）.

【教师活动】先分析问题，指出证明点P在线段AC的垂直平分线上，即证明点P到线段AC两端点的距离相等即可.

【学生活动】写出证明过程，小组内交流，总结三角形角平分线的交点到具有的特点，进行总结.

【互动结论】三角形三边垂直平分线交于一点，这一点到三角形三个顶点的距离相等.

典型例题

例3   在△ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC于E，l1与l2相交于点O.△ADE的周长为6 cm.

（1）求证：AD＝BD，AE＝CE；

（2）求BC的长；

（3）分别连结OA、OB、OC，若△OBC的周长为16 cm，求OA的长.

（1）证明：∵ l1是AB边的垂直平分线，l2是AC边的垂直平分线，

∴ AD＝BD，AE＝CE；

（2）解：△ADE的周长为6，

∴ AD+DE+EA＝6，

∴ BD+DE+EC＝BC＝6；

（3）解：∵ l1是AB边的垂直平分线，l2是AC边的垂直平分线，

∴ OB＝OA，OC＝OA，

△OBC的周长为16，

∴ OB+OC+BC＝16，

∴ OB+OC＝16﹣6＝10，

∴ OA＝OB＝OC＝5.

【教师活动】巡视学生做题，提示线段垂直平分线的性质定理的应用.

【学生活动】先独立思考，再小组交流.

课堂练习

1.在锐角三角形 ABC 内一点P，满足 PA＝PB＝PC,则点P是△ABC（   ）   

A.三条角平分线的交点      B.三条中线的交点

C.三条高的交点            D.三边垂直平分线的交点

2.已知线段AB，在平面上找到三个点D、E、F，使DA＝DB，EA＝EB,FA＝FB，这样的点的组合共有　　　　种.

3.下列说法：

① 若点P、E是线段AB的垂直平分线上两点，则EA＝EB，PA＝PB；

②若PA＝PB，EA＝EB，则直线PE垂直平分线段AB；

③若PA＝PB，则点P必是线段AB的垂直平分线上的点；

④若EA＝EB，则经过点E的直线垂直平分线段AB.

其中正确的有               （填序号）.

4.如图，△ABC中，AB＝AC,AB的垂直平分线交AC于E,连接BE，AB+BC＝16cm,则△BCE的周长是        cm.

5.已知：如图，点C，D是线段AB外的两点，且AC ＝BC，  AD＝BD，AB与CD相交于点O.

  求证：AO＝BO.

6.如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF 的关系.

参考答案

1.D  2.无数   3.①②③ 

4.16　解析：因为DE是AB的垂直平分线，

所以AE＝BE，因为AB＝AC，AB+BC＝16 cm,所以AC+BC＝16 cm，

所以△BCE的周长＝BC+BE+CE＝BC+CE+AE＝BC+AC＝16 cm.

5.证明：∵  AC ＝BC，AD＝BD，

∴ 点C和点D在线段AB的垂直平分线上，

∴  CD为线段AB的垂直平分线.

又 ∵ AB与CD相交于点O，

∴ AO＝BO.

6. 解： AD垂直平分EF.

∵ AD平分∠BAC，DE⊥AB，DF⊥AC，

∴ ∠EAD＝∠FAD，∠AED＝∠AFD＝90°.

又∵ AD＝AD，∴ △ADE≌△ADF，

∴ AE＝AF，DE＝DF.

∴ A、D均在线段EF的垂直平分线上，

即直线AD垂直平分线段EF.

课堂小结

布置作业

教材习题15.2第1,2,3,4题.

板书设计

15.2　线段的垂直平分线

1.线段垂直平分线的性质.

2.线段垂直平分线的判定.

3.三角形三边垂直平分线交于一点，这一点到三角形三个顶点的距离相等.

教学反思

教学反思

教学反思

教学反思

教学反思

教学反思

教学反思