初中数学人教版八年级上册12.2 三角形全等的判定课文课件ppt

这是一份初中数学人教版八年级上册12.2 三角形全等的判定课文课件ppt，共34页。PPT课件主要包含了用符号语言表达为，摆齐条件，得结论，2三条边，1三个角，3两边一角，4两角一边，SSS，连接B′C′，边边角等内容，欢迎下载使用。

1、探索并理解“边角边”判定方法。2、会用“边角边”判定方法证明三角形全等。3、会用边角边定理来解决单数学问题。
探索并正确理解三角形全等的判定方法“SAS”。
用“SAS” 判定方法进行简单的应用。
1.边角边判定三角形全等的方法是怎样的？2.你会用边角边来证明用三角全等吗？3.你会用边角边来作一个三角形等于已知三角形吗？
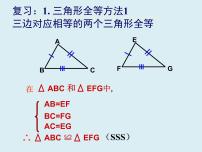
三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）。
在△ABC和△DEF中
∴ △ABC≌△DEF（SSS）
三角形全等判定方法1
除了SSS外,还有其他情况吗？继续探索三角形全等的条件.
当两个三角形满足六个条件中的三个时，有四种情况:
思考：已知一个三角形的两条边和一个角，那么这两条边与这一个角的位置上有几种可能性呢？
在图一中， ∠A是AB和AC的夹角，
符合图一的条件，它可称为“两边夹角”。
符合图二的条件， 通常说成“两边和其中一边的对角”
已知△ABC，画一个△A′B′C′使AB =A′B′,AC =A′C ′, ∠A=∠A′。
结论:两边及夹角对应相等的两个三角形全等
思考： ① △A′B′C′与△ABC全等吗？如何验正？
画法: 1.画 ∠DA′E=∠A；
2.在射线A D上截取A′B′=AB,在射线A′E上截取A′C′=AC;
思考： ②这两个三角形全等是满足哪三个条件？
三角形全等判定方法2
在△ABC与△DEF中
∴△ABC≌△DEF（SAS）
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
在下列图中找出全等三角形
两边及其中一边的对角对应相等的两个三角形全等吗?
已知：AC=10cm,BC=8cm, ∠A=45 °.
△ABC的形状与大小是唯一确定的吗?
显然： △ABC与△AB’C不全等
①两边及夹角对应相等的两个三角形全等（SAS)；
②两边及其中一边的的对角对应相等的两个三角形不一定全等．
③ 现在你知道哪些三角形全等的判定方法？
两边及一角对应相等的两个三角形全等吗？
例 如图，AC=BD，∠CAB=∠DBA，你能判断BC=AD吗？说明理由。
证明:在△ABC与△BAD中
AC=BD∠CAB=∠DBAAB=BA
∴△ABC≌△BAD（SAS）
∴BC=AD (全等三角形的对应边相等）
1、在下列推理中填写需要补充的条件，使结论成立：如图,在△AOB和△DOC中
AO=DO(已知)______=________( )BO=CO(已知)∴ △AOB≌△DOC（ ）
2.如图，在△AEC和△ADB中，已知AE=AD，AC=AB，请说明△AEC≌△ADB的理由。
____=____ (已知) ∠A= ∠A( 公共角) _____=____(已知)∴ △AEC≌△ADB（ ）
解：在△AEC和△ADB中
1.若AB=AC，则添加什么条件可得△ABD≌△ACD?
2.如图，要证△ACB≌△ADB，至少选用哪些条件可证得△ACB≌△ADB
∠CAB= ∠ DAB
3、如图，AB＝CD，AB∥CD，E，F是BD上两点且BE＝DF，则图中全等的三角形有(　　)A．1对 B．2对 C．3对 D．4对
4、如图，若线段AB，CD互相平分且相交于点O，则下列结论错误的是(　　)A．AD＝BC B．∠C＝∠DC．AD∥BC D．OB＝OC
5、如图，已知：AB＝AD，AC＝AE，∠1＝∠2，求证：(1)△ABC≌△ADE； (2)∠B＝∠D.
证明：(1)∵∠1＝∠2，∴∠1＋∠EAC＝∠2＋∠EAC，即∠BAC＝∠DAE，
在△ABC和△ADE中，
(2)∵△ABC≌△ADE，∴∠B＝∠D
∴△ABC≌△ADE（SAS）　
AB=AD ∠BAC=∠DAE AC=AE
6.如图:己知AD∥BC,AF=CE,AD=BC,E、F都在直线AC上，试说明DE∥BF。
∴AF-EF=CE-EF
在△ADE和△CBF中
AD=CB∠A=∠CAE=CF
∴△ADE≌△CBF（SAS）　
1．如图，已知AB＝AC，AD＝AE，∠BAC＝∠DAE，下列结论不正确的是(　　)A．∠BAD＝∠CAE B．△ABD≌△ACEC．AB＝BC D．BD＝CE
2．如图，已知AB∥CD，AB＝CD，AE＝FD，则图中的全等三角形有(　　)A．1对 B．2对 C．3对 D．4对
3．两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AD＝CD，AB＝CB.小明在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO＝CO＝ AC；③△ABD≌△CBD.其中正确的结论有(　　)A．0个 B．1个 C．2个 D．3个
4．如图，在△ABC中，AB＝AC，点E，F在边BC上，BE＝CF，点D在AF的延长线上，AD＝AC.(1)求证△ABE≌△ACF；
证明：∵AB＝AC，∴∠B＝∠ACF.
在△ABE和△ACF中，
∴△ABE≌△ACF (SAS)．
(2)若∠BAE＝30°，则∠ADC＝_____°.
5．如图①，点M，N分别是正五边形ABCDE的边BC，CD上的点，且BM＝CN，AM交BN于点P.(1)求证△ABM≌△BCN；
证明：∵五边形ABCDE是正五边形， ∴AB＝BC，∠ABM＝∠C.
在△ABM和△BCN中，
∴△ABM≌△BCN (SAS)．
解：由(1)可知△ABM≌△BCN，∴∠BAM＝∠CBN.∴∠APN＝∠BAP＋∠ABP ＝∠CBN＋∠ABN ＝∠ABC＝ ＝108°.
(2)求∠APN的度数；
(3)将上述正五边形改成正六边形，如图②所示，若其他条件不变，则∠APN的度数为________．
6．如图,在△ABC中，AB＞AC，AD是BC边上的中线．求证： (AB－AC)＜AD< (AB＋AC)．
证明：如图，延长AD至点E，使DE＝AD，连接BE.
∵AD是BC边上的中线，∴CD＝BD.
在△ACD和△EBD中，
∴△ACD≌△EBD (SAS)．
在△ABE中，AB－BE＜AE1．如图，AB与CD相交于点E，AE＝CE，DE＝BE.求证∠A＝∠C.
2．如图，AB∥CD，AB＝CD，CE＝BF.请写出DF与AE的数量关系，并证明你的结论．