人教版七年级上册第一章 有理数1.3 有理数的加减法1.3.2 有理数的减法优秀课件ppt

这是一份人教版七年级上册第一章 有理数1.3 有理数的加减法1.3.2 有理数的减法优秀课件ppt，共15页。PPT课件主要包含了情景导入，探究新知，减法转化成加法，按有理数加法法则计算，-27+8，-20-7+3+5，省略括号，归纳总结，小试牛刀，交流探究等内容，欢迎下载使用。

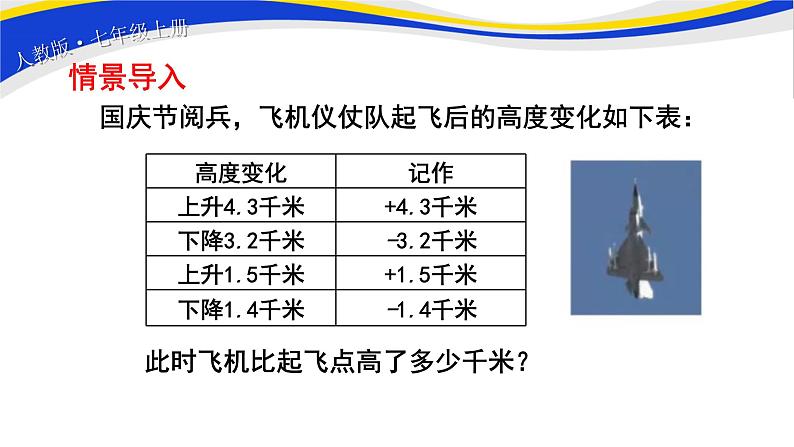
国庆节阅兵，飞机仪仗队起飞后的高度变化如下表：
此时飞机比起飞点高了多少千米？
方法一：①4.3+(-3.2)+1.5+(-1.4) =1.1+1.5+(-1.4)　=2.6+(-1.4)　=1.2(千米).
方法二：②4.3-3.2+1.5-1.4　 =1.1+1.5-1.4　 =2.6-1.4　 =1.2(千米).
比较以上两种算法，你发现了什么？
例1 计算 （-20）+（+3)-(-5)-(+7)
（-20） +（+3) -(-5) -(+7)=（-20）+（+3)+(+5)+(-7)=[（-20）+(-7)]+（+3)+(+5)=(-27)+(+8)=-19
引入相反数后，加减混合运算可以统一为加法运算.a+b-c=a+b+(-c)
像上面的式子读作“负20、正3、正5、负7的和”，按运算意义也可读作“负20加3加5减7”，在这里把除第一个数外的数字前面的符号都可看作为运算符号，又可看作性质符号.这样，性质符号与运算符号既有区别，又有联系，有时可以互相转化.
（-20）+（+3)+(+5)+(-7)
=-20+3+5-7　　
例题(-20)+(+3)-(-5)-(+7)的运算过程也可以简单地写为:
(-20)+(+3)-(-5)-(+7)
运用加法交换律使同号两数分别相加
第一步：写成省略加号的形式；第二步：运用加法交换律，交换加数的位置；第三步：适当运用加法结合律进行运算.
在交换加数位置时，要连同加数前面的符号一起交换. 一般正数与正数、负数与负数先相加； 化合成整数的先相加； 互为相反数的先相加； 同分母的先相加.
有理数的加减混合运算的步骤：
解：原式 =（-0.5）+（+0.25）+（+2.75）+（-5.5） =-0.5+0.25+2.75-5.5 =（-0.5-5.5）+（0.25+2.75） =-6+3 =-3
注意：在式子中若既有分数又有小数，把小数统一成分数或把分数统一成小数
在数轴上，点A，B分别表示数a，b. 利用有理数减法，分别计算下列情况下点A，B之间的距离： a=2，b=6；a=0，b=6；a=2，b=-6；a=-2，b=-6. 你能发现点A，B之间的距离与数a，b之间的关系吗？
两点之间的距离等于这两个数差的绝对值，即AB=|a-b|.
下表是某年某市汽油价格的调整情况：
注：正号表示比前一次上调，负号表示比前一次下降.
问：与上一年年底相比，11月9日汽油价格是上升了还是下降了？变化了多少元？
解：-140+290+400+600-220+300-190+480=1520（元）答：与上一年年底相比，11月9日汽油价格上升了1520元.
把加减法统一成加法再进行计算