人教A版 (2019)必修 第一册3.1 函数的概念及其表示第1课时导学案

这是一份人教A版 (2019)必修 第一册3.1 函数的概念及其表示第1课时导学案，共12页。学案主要包含了知识导学，新知拓展等内容，欢迎下载使用。

3.1.2　函数的表示法
第1课时　函数的表示法
(教师独具内容)
课程标准：1.了解函数的三种表示方法及各自的优缺点.2.通过实例了解分段函数的概念.3.掌握求函数解析式的常见方法．
教学重点：1.函数的三种表示方法.2.根据条件求函数的解析式．
教学难点：用解析法和图象法表示分段函数.

【知识导学】
知识点一　　　函数的表示法
(1)解析法：用数学表达式表示两个变量之间的对应关系．
(2)列表法：列出表格来表示两个变量之间的对应关系．
(3)图象法：用图象表示两个变量之间的对应关系．
知识点二　　　描点法作函数图象的三个步骤
(1)列表：先找出一些有代表性的自变量x的值，再计算出与这些自变量x相对应的函数值f(x)，并用表格的形式表示出来．
(2)描点：把第(1)步表格中的点(x，f(x))一一在平面直角坐标系中描出来．
(3)连线：用光滑的曲线把这些点按自变量由小到大(或由大到小)的顺序连接起来．
知识点三　　　分段函数的概念
如果函数y＝f(x)，x∈A，根据自变量x在A中不同的取值范围，有着不同的对应关系，那么称这样的函数为分段函数．
【新知拓展】
1．函数三种表示法的几点说明
(1)解析法：变量间的对应关系明确，且要注意函数的定义域．
(2)列表法：就是列出表格来表示两个变量之间的对应关系．比如我们生活中经常遇到的列车时刻表、银行的利率表等．其优点是不需要计算就可以直接看出与自变量相对应的函数值．这种表示法常常被应用到实际生产和生活中去．
(3)图象法：函数图象的形状不一定是一条或几条无限长的平滑曲线，也可能是一些点、一些线段、一段曲线等，但不是任何一个图形都是函数图象．
2．分段函数的特点
(1)分段函数是一个函数，并非几个函数．
(2)分段函数的定义域是各段定义域的并集．
(3)分段函数的值域是各段值域的并集．
(4)分段函数的图象要分段来画．

1．判一判(正确的打“√”，错误的打“×”)
(1)任何一个函数都可以用列表法表示．(　　)
(2)任何一个函数都可以用解析法表示．(　　)
(3)分段函数是几个函数，而不是一个函数．(　　)
(4)函数的图象可以是一条水平直线．(　　)
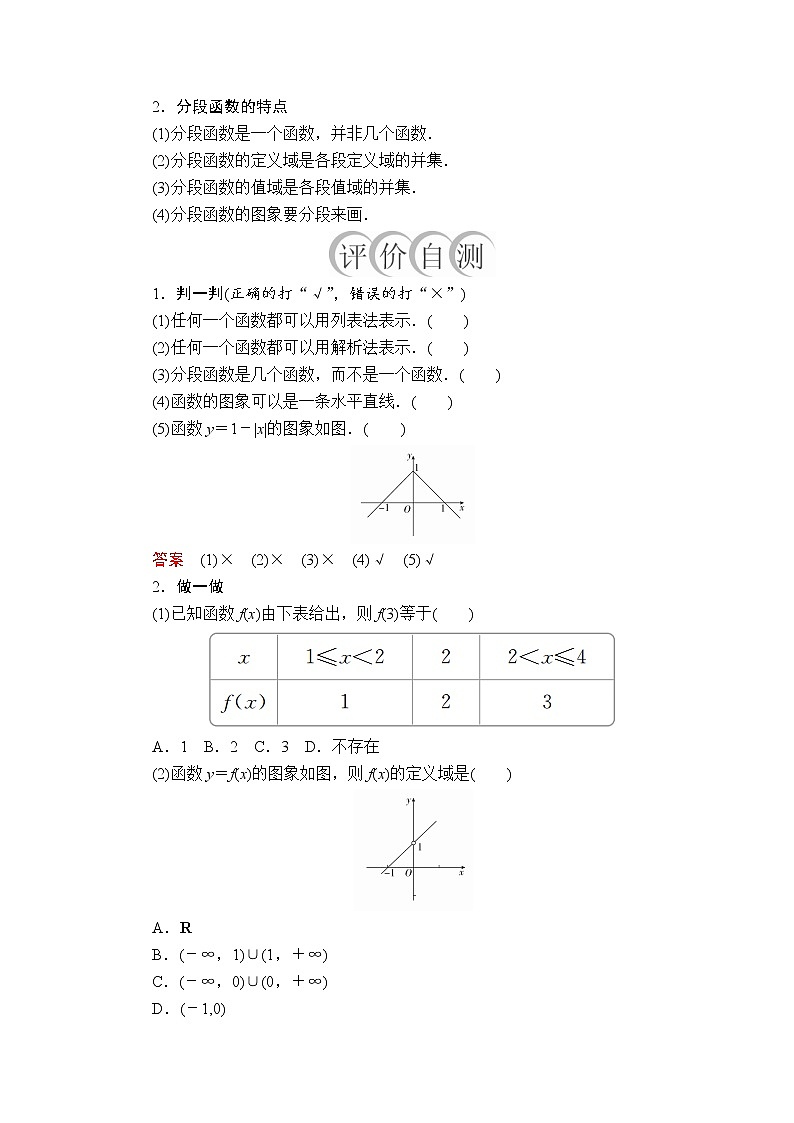
(5)函数y＝1－|x|的图象如图．(　　)

答案　(1)×　(2)×　(3)×　(4)√　(5)√
2．做一做
(1)已知函数f(x)由下表给出，则f(3)等于(　　)

A．1 B．2 C．3 D．不存在
(2)函数y＝f(x)的图象如图，则f(x)的定义域是(　　)

A．R
B．(－∞，1)∪(1，＋∞)
C．(－∞，0)∪(0，＋∞)
D．(－1,0)
(3)已知反比例函数f(x)满足f(3)＝－6，f(x)的解析式为________．
(4)已知函数f(x)＝则f(3)＝________.
(5)已知f(x)＝若f(x0)＝4，则x0＝________.
答案　(1)C　(2)C　(3)f(x)＝－　(4)1　(5)－2或1

题型一 函数的表示法
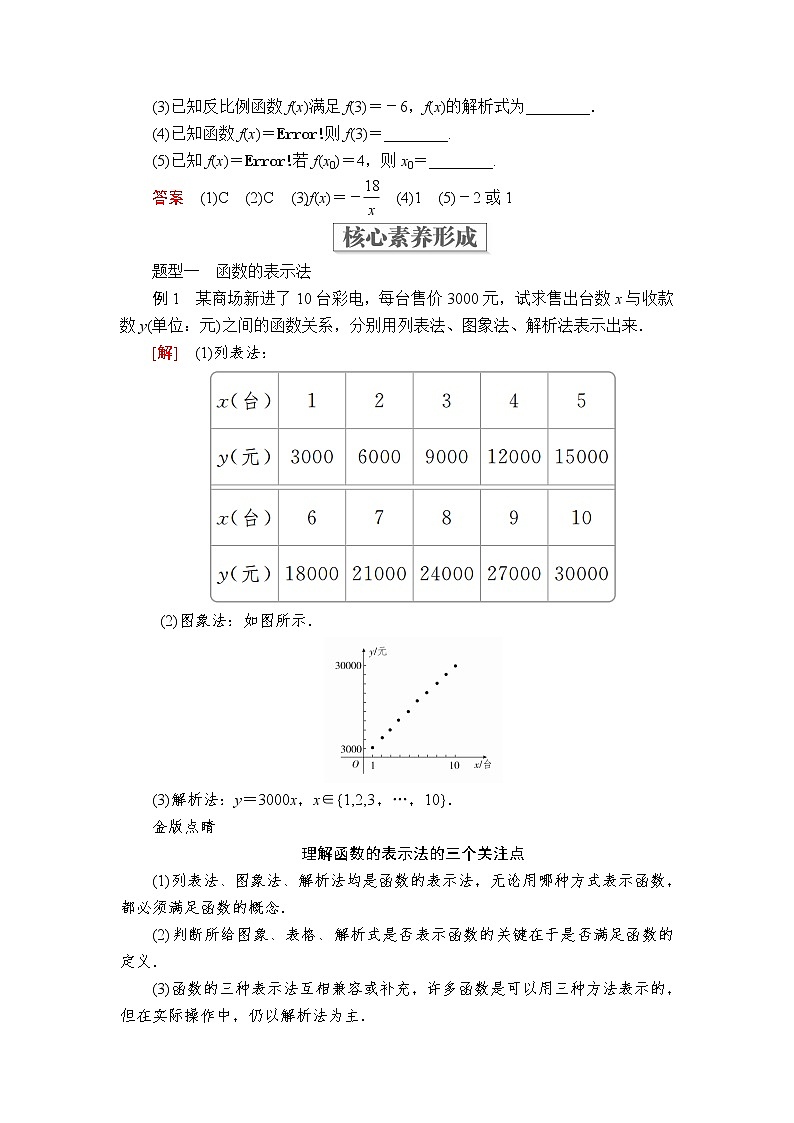
例1　某商场新进了10台彩电，每台售价3000元，试求售出台数x与收款数y(单位：元)之间的函数关系，分别用列表法、图象法、解析法表示出来．
[解]　(1)列表法：

(2)图象法：如图所示．

(3)解析法：y＝3000x，x∈{1,2,3，…，10}．
金版点睛
理解函数的表示法的三个关注点
(1)列表法、图象法、解析法均是函数的表示法，无论用哪种方式表示函数，都必须满足函数的概念．
(2)判断所给图象、表格、解析式是否表示函数的关键在于是否满足函数的定义．
(3)函数的三种表示法互相兼容或补充，许多函数是可以用三种方法表示的，但在实际操作中，仍以解析法为主．

　已知函数f(x)，g(x)分别由下表给出．

则f[g(1)]的值为________；
当g[f(x)]＝2时，x＝________.
答案　1　1
解析　由于函数关系是用表格形式给出的，知g(1)＝3，
∴f[g(1)]＝f(3)＝1；
由于g(2)＝2，∴f(x)＝2，∴x＝1.
题型二 函数图象的作法及应用
例2　作出下列函数的图象并求出其值域．
(1)y＝，x∈[2，＋∞)；
(2)y＝x2＋2x，x∈[－2,2]；
(3)y＝
(4)y＝|x＋1|＋|x－3|.
[解]　(1)列表：


画图象，当x∈[2，＋∞)时，图象是反比例函数y＝的一部分(图①)，观察图象可知其值域为(0,1]．

(2)列表：

画图象，图象是抛物线y＝x2＋2x在－2≤x≤2之间的部分(图②)．由图可得函数的值域是[－1,8]．

(3)函数y＝的图象如图③所示，观察图象，得函数的值域为(1，＋∞)．
　　
(4)将原函数式中的绝对值符号去掉，化为分段函数为y＝的图象如图④所示．观察图象，得函数的值域为[4，＋∞)．
金版点睛
作函数图象的方法
(1)若函数是一次函数、二次函数、反比例函数等，则可根据函数图象特征描出图象上的几个关键点，直接画出图象即可，有些可能需要根据定义域进行取舍．
(2)若函数是复合函数，则要按：①列表；②描点；③连线三个基本步骤作出函数的图象.
(3)对含有绝对值的函数，要作出其图象，首先应根据绝对值的意义去掉绝对值符号，将函数转化为分段函数，然后分段作出函数图象.
(4)作分段函数的图象时，分别作出各段的图象，在作每一段图象时，可先不管定义域的限制，作出其图象，再保留定义域内的一段图象即可，作图时要特别注意接点处点的虚实，保证不重不漏.
　作出下列函数图象，并求其值域：
(1)y＝1－x(x∈Z，且|x|≤2)；
(2)y＝2x2－4x－3(0≤x<3)；
(3)y＝(－2≤x≤1，且x≠0)．
解　(1)因为x∈Z，且|x|≤2，所以x∈{－2，－1,0,1,2}．
所以该函数图象为一直线上的孤立点(如图①)．
由图象知，y∈{－1,0,1,2,3}．
(2)因为y＝2(x－1)2－5，
所以当x＝0时，y＝－3；当x＝3时，y＝3；
当x＝1时，y＝－5.
因为x∈[0,3)，故图象是一段抛物线(如图②)．
由图象可知，y∈[－5,3)．

(3)用描点法可以作出函数的图象如图③.
由图可知y＝(－2≤x≤1，且x≠0)的值域为(－∞，－1]∪[2，＋∞).
题型三 求函数的解析式
例3　(1)已知f(x)是一次函数，且f[f(x)]＝9x＋4，求f(x)的解析式；
(2)已知函数f(x＋1)＝x2－2x，求f(x)的解析式；
(3)已知函数y＝f(x)满足f(x)＋2f＝x，求函数y＝f(x)的解析式；
(4)设f(x)是R上的函数，且满足f(0)＝1，并且对任意的实数x，y都有f(x－y)＝f(x)－y(2x－y＋1)，求f(x)的解析式．
[解]　(1)设f(x)＝kx＋b(k≠0)，
则f[f(x)]＝k(kx＋b)＋b＝k2x＋kb＋b＝9x＋4.
∴解得或
∴f(x)＝3x＋1或f(x)＝－3x－2.
(2)解法一(换元法)：令x＋1＝t，则x＝t－1，t∈R，可得f(t)＝(t－1)2－2(t－1)＝t2－4t＋3，即f(x)＝x2－4x＋3.
解法二(配凑法)：因为x2－2x＝(x2＋2x＋1)－(4x＋4)＋3＝(x＋1)2－4(x＋1)＋3，所以f(x＋1)＝(x＋1)2－4(x＋1)＋3，即f(x)＝x2－4x＋3.
(3)在已知等式中，将x换成，得f＋2f(x)＝，与已知方程联立，得
解得f(x)＝－＋.
(4)解法一：由已知条件得f(0)＝1，
又f(x－y)＝f(x)－y(2x－y＋1)，
设y＝x，则f(x－y)＝f(0)＝f(x)－x(2x－x＋1)，
所以f(x)＝x2＋x＋1.
解法二：令x＝0，得f(0－y)＝f(0)－y(－y＋1)，
即f(－y)＝1－y(－y＋1)，
将－y用x代换得f(x)＝x2＋x＋1.
金版点睛
函数解析式的求法
求函数解析式，关键是对基本方法的掌握，常用方法有配凑法、换元法、待定系数法、解方程(组)法、赋值法等．
(1)配凑法：将形如f[g(x)]的函数的表达式配凑为关于g(x)的表达式，并整体将g(x)用x代换，即可求出函数f(x)的解析式．如由f(x＋1)＝(x＋1)2可得f(x)＝x2.
(2)换元法：将函数f[g(x)]中的g(x)用t表示，则可求得x关于t的表达式，并将最终结果中的t用x代换，即可求得函数f(x)的解析式．
(3)待定系数法：将已知类型的函数以确定的形式表达，并利用已知条件求出其中的参数，从而得到函数的解析式．
一次函数解析式为y＝ax＋b(a≠0)．二次函数解析式为y＝ax2＋bx＋c(a≠0)．
(4)解方程(组)法：采用解方程或方程组的方法，消去不需要的函数式子，得到f(x)的表达式，这种方法也称为消去法．
(5)赋值法：利用恒等式将特殊值代入，求出特定函数的解析式．这种方法灵活性强，必须针对不同的类型选取不同的特殊值．

　(1)已知函数f(x)＝x2，g(x)为一次函数，且一次项系数大于零，若f[g(x)]＝4x2－20x＋25，求g(x)的表达式；
(2)已知f(＋1)＝x＋2，求f(x)的解析式；
(3)已知f(x)＋2f(－x)＝x2＋2x，求f(x)；
(4)设f(x)是R上的函数，f(0)＝1，并且对于任意的实数x，y都有f(x＋y)＝f(x)＋y(2x＋1)，求f(x)．
解　(1)由g(x)为一次函数，设g(x)＝ax＋b(a>0)，
∵f[g(x)]＝4x2－20x＋25，
∴(ax＋b)2＝4x2－20x＋25，
即a2x2＋2abx＋b2＝4x2－20x＋25，
从而a2＝4,2ab＝－20，b2＝25，
解得a＝2，b＝－5，故g(x)＝2x－5(x∈R)．
(2)解法一(配凑法)：
∵f(＋1)＝x＋2＝(＋1)2－1(＋1≥1)，
∴f(x)＝x2－1(x≥1)．
解法二(换元法)：
令＋1＝t(t≥1)，则x＝(t－1)2(t≥1)，
∴f(t)＝(t－1)2＋2(t－1)＝t2－1(t≥1)．
∴f(x)＝x2－1(x≥1)．
(3)将f(x)＋2f(－x)＝x2＋2x中的x用－x替换，得f(－x)＋2f(x)＝x2－2x.于是得到关于f(x)，f(－x)的方程组
解得f(x)＝x2－2x.
(4)由已知条件得f(0)＝1，又f(x＋y)＝f(x)＋y(2x＋1)，
设y＝－x，
则f(x－x)＝f(x)＋(－x)(2x＋1)，
∴f(x)＝2x2＋x＋1.
题型四 根据图象求分段函数的解析式
例4　根据如图所示的函数f(x)的图象，写出函数的解析式．

[解]　当－3≤x<－1时，设f(x)＝ax＋b(a≠0)，将点(－3,1)，(－1，－2)代入，可得f(x)＝－x－；
当－1≤x<1时，同理，可设f(x)＝cx＋d(c≠0)，将点(－1，－2)，(1,1)代入，可得f(x)＝x－；
当1≤x<2时，f(x)＝1.
所以f(x)＝
金版点睛
由图象求函数的解析式，需充分挖掘图象中提供的点的坐标，合理利用待定系数法求解.对于分段函数，需观察各段图象的端点是空心点还是实心点，正确写出各段解析式对应的自变量的范围.

　已知函数y＝f(x)的图象是由图中的两条射线和抛物线的一部分组成的，求此函数的解析式．

解　设左侧的射线对应的解析式为y＝kx＋b(x≤1)．
∵点(1,1)，(0,2)在射线上，
∴解得
∴左侧射线对应的函数的解析式为y＝－x＋2(x≤1)．
同理，当x≥3时，函数的解析式为y＝x－2(x≥3)．
设抛物线的一部分对应的二次函数的解析式为y＝a(x－2)2＋2(1 ∵点(1,1)在抛物线上，∴a＋2＝1，即a＝－1.
∴当1 综上，函数的解析式为y＝
题型五 分段函数求值
例5　(1)设f(x)＝则f(5)的值是(　　)
A．24 B．21 C．18 D．16
(2)设函数f(x)＝则f[f(3)]＝(　　)
A. B．3 C. D.
(3)已知函数f(x)＝若f(x)＝－3，则x＝________.
[解析]　(1)f(5)＝f[f(10)]，f(10)＝f[f(15)]＝f(18)＝21，f(5)＝f(21)＝24.
(2)∵f(3)＝<1，
∴f[f(3)]＝2＋1＝.
(3)若x≤1，由x＋1＝－3，得x＝－4.
若x>1，由1－x2＝－3，得x2＝4，
解得x＝2或x＝－2(舍去)．
综上可得，所求x的值为－4或2.
[答案]　(1)A　(2)D　(3)－4或2
金版点睛
1．求分段函数函数值的方法
(1)先确定要求值的自变量属于哪一段区间．
(2)然后代入该段的解析式求值，直到求出值为止．
2．已知函数值求字母取值的步骤
(1)先对字母的取值范围分类讨论．
(2)然后代入到不同的解析式中．
(3)通过解方程求出字母的值．
(4)检验所求的值是否在所讨论的区间内．
3．若题目是含有多层“f”的问题，要按照“由里到外”的顺序，层层处理．

　(1)已知函数f(x)＝若f[f(0)]＝a，则实数a＝________；
(2)已知f(x)＝求f{f[f(－3)]}．
答案　(1)　(2)见解析
解析　(1)依题意知f(0)＝3×0＋2＝2，则f[f(0)]＝f(2)＝22－2a＝a，求得a＝.
(2)∵－3<0，∴f(－3)＝0，
∴f[f(－3)]＝f(0)＝π.
又π>0，∴f{f[f(－3)]}＝f(π)＝π＋1，
即f{f[f(－3)]}＝π＋1.
　　　　　　　　　　　　　　　　　　

1．已知函数y＝f(x)的对应关系如下表，函数y＝g(x)的图象是如图的曲线ABC，其中A(1,3)，B(2,1)，C(3,2)，则f[g(2)]的值为(　　)

A．3 B．2 C．1 D．0
答案　B
解析　由函数g(x)的图象知，g(2)＝1，则f[g(2)]＝f(1)＝2.
2．下列图形是函数y＝x|x|的图象的是(　　)

答案　D
解析　∵f(x)＝分别画出y＝x2(取x≥0部分)及y＝－x2(取x<0部分)即可．
3．对a，b∈R，记max{a，b}＝函数f(x)＝max{|x＋1|，|x－2|}(x∈R)的最小值是(　　)
A．0 B. C. D．3
答案　C
解析　分别作出y＝|x＋1|和y＝|x－2|的图象，则实线部分为f(x)的图象，由图象可得，其最小值为.故选C.

4．如图，函数f(x)的图象是折线段ABC，其中点A，B，C的坐标分别为(0,4)，(2,0)，(4,2)，则f{f[f(2)]}＝________，f(x)的值域是________．

答案　2　[0,4]
解析　∵f(2)＝0，∴f[f(2)]＝f(0)＝4，
∴f{f[f(2)]}＝f(4)＝2.
由图象可知，f(x)的值域是[0,4]．
5．已知f(x)＝x＋b，f(ax＋1)＝3x＋2，求a，b的值．
解　由f(x)＝x＋b，得f(ax＋1)＝ax＋1＋b.
∴ax＋1＋b＝3x＋2，∴a＝3，b＋1＝2，即a＝3，b＝1.