数学九年级上册4.一元二次方程根的判别式教学ppt课件

这是一份数学九年级上册4.一元二次方程根的判别式教学ppt课件，共14页。PPT课件主要包含了新课引入，知识回顾，新课讲解，反之同样成立，随堂即练，课堂总结等内容，欢迎下载使用。

1.了解一元二次方程根的判别式.（重点）2.会判断一元二次方程根的情况. (难点)3.掌握一元二次方程根的判别式的应用.（难点）
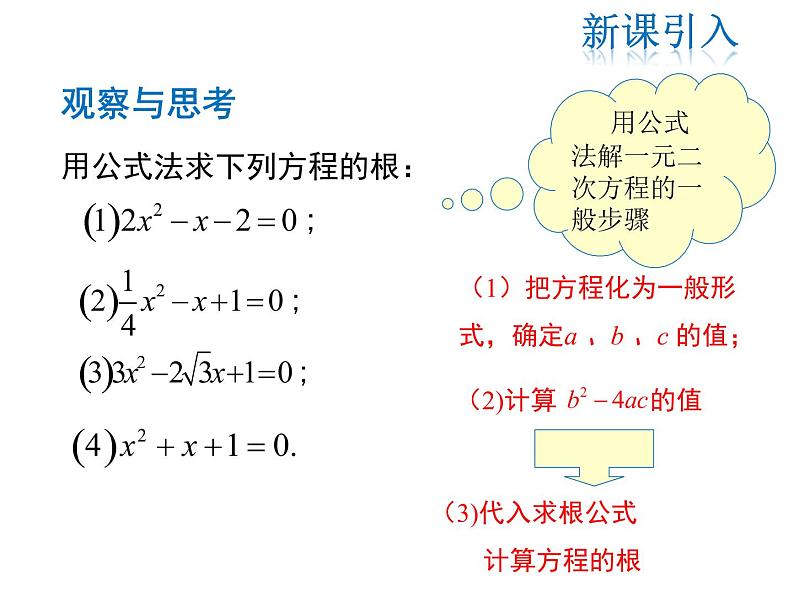
用公式法求下列方程的根：
用公式法解一元二次方程的一般步骤
（1）把方程化为一般形 式，确定a 、b 、c 的值；
一般地，对于一元二次方程 如果 ，那么方程的两个根为
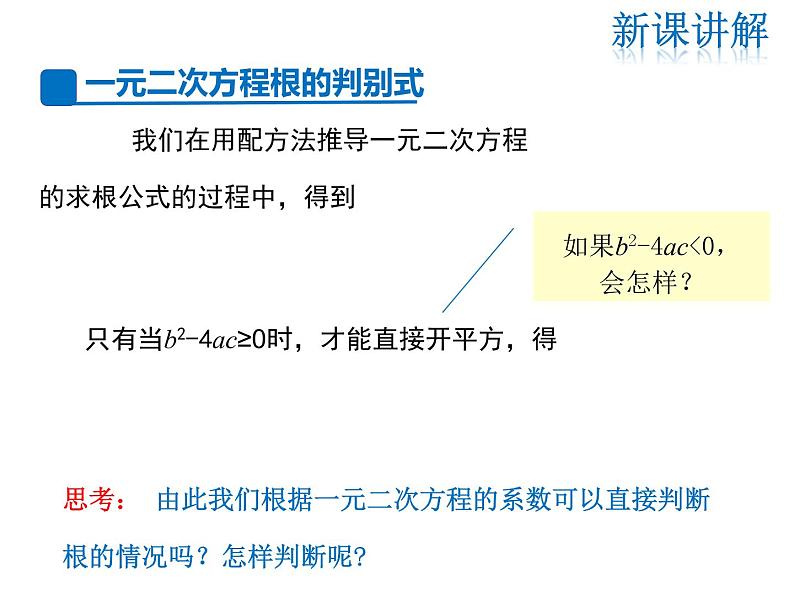
我们在用配方法推导一元二次方程 的求根公式的过程中，得到
只有当b2-4ac≥0时，才能直接开平方，得
如果b2-4ac<0，会怎样？
思考： 由此我们根据一元二次方程的系数可以直接判断根的情况吗？怎样判断呢?
想一想：究竟是谁决定了一元二次方程根的情况?
2.当方程有两个相等的实数根时，有 ；
反过来，对于一元二次方程 有：
我们把b2-4ac叫做一元二次方程ax2+bx+c=0（a≠0）的根的判别式，常用符号“∆”来表示，用它可以直接判断一元二次方程ax2+bx+c=0（a≠0）的实数根的情况：
当∆＞0 时，方程有两个不相等的实数根；
当∆=0 时，方程有两个相等的实数根；
当∆＜0 时，方程没有实数根.
不解方程，判断下列方程的根的情况：
3.判断根的情况，得出结论.
2.计算∆的值，确定∆的符号；
★不解方程，判别一元二次方程的根的情况的一般 步骤
1.不解方程，判别下列方程的根的情况：
2.不解方程，判别关于x的方程 的根的情况.
一元二次方程ax2+bx+c=0（a≠0）的根的情况