2021学年1.1.2集合间的基本关系教课课件ppt

这是一份2021学年1.1.2集合间的基本关系教课课件ppt，共33页。PPT课件主要包含了A＝123，B＝127，示例2，集合相等，A＝B，AB，真子集，B是A的真子集，练习2，子集的传递性等内容，欢迎下载使用。

实数有相等关系，大小关系，类比实数之间的关系，集合之间是否具备类似的关系？
示例1：观察下面三个集合, 找出它们之间的关系:
C＝{1，2，3，4，5}
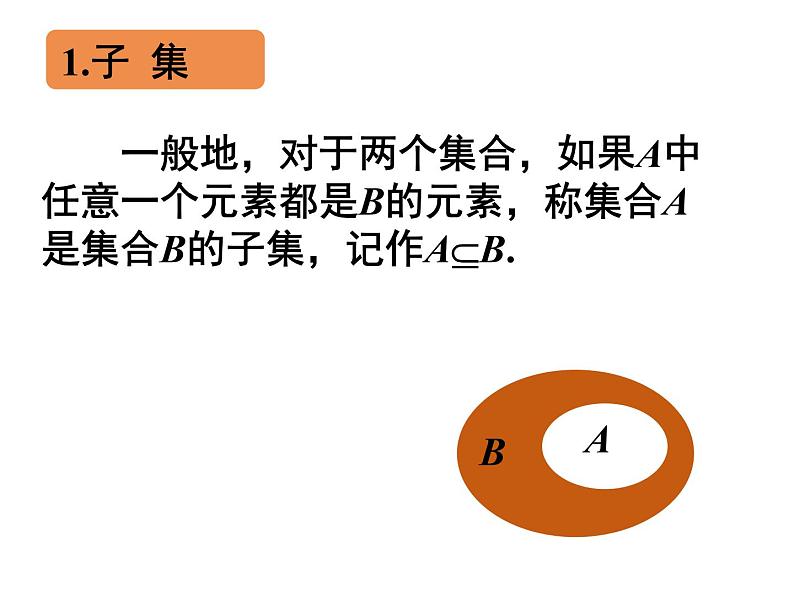
一般地，对于两个集合，如果A中任意一个元素都是B的元素，称集合A是集合B的子集，记作AB.
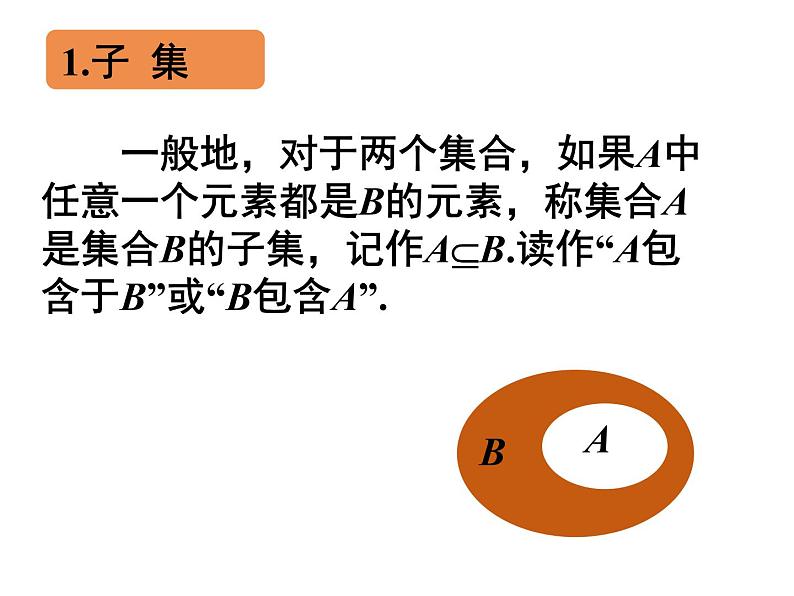
一般地，对于两个集合，如果A中任意一个元素都是B的元素，称集合A是集合B的子集，记作AB.读作“A包含于B”或“B包含A”.
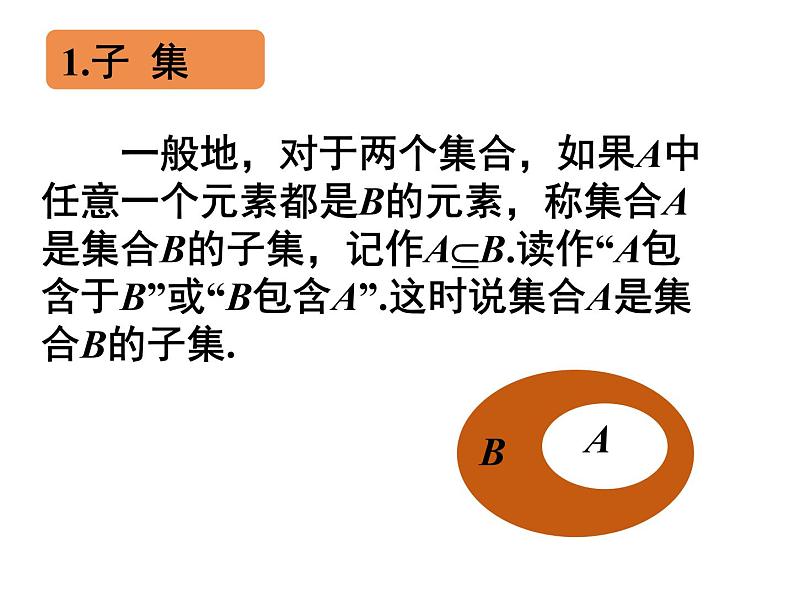
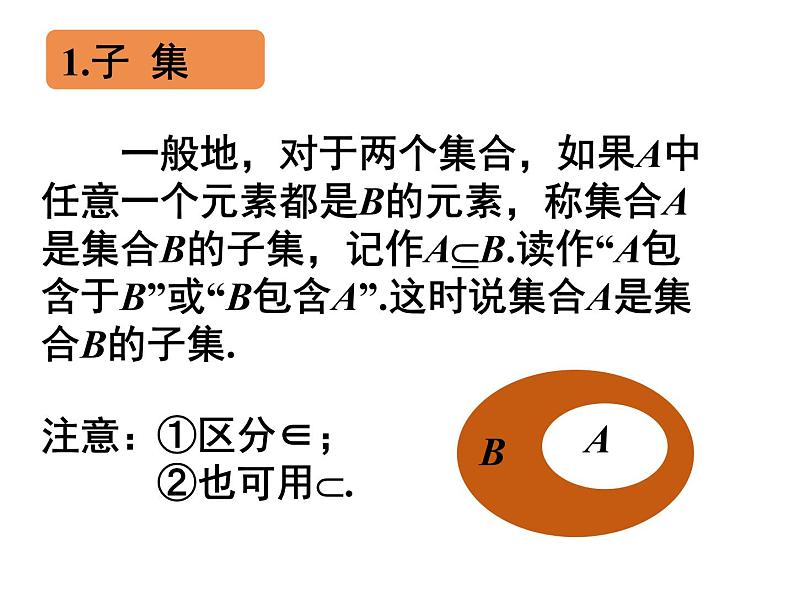
一般地，对于两个集合，如果A中任意一个元素都是B的元素，称集合A是集合B的子集，记作AB.读作“A包含于B”或“B包含A”.这时说集合A是集合B的子集.
①区分∈；②也可用.
这时, 我们说集合A是集合C的子集.
而从B与C来看，显然B不包含于C.
A＝{ x|x是两边相等的三角形}，B＝{ x|x是等腰三角形}，
A＝{ x|x是两边相等的三角形}，B＝{ x|x是等腰三角形}，有AB，BA，则A＝B.
若AB，BA，则A＝B.
练习1：观察下列各组集合，并指明两个集合的关系① A＝Z ，B＝N；
③ A＝{x|x2－3x＋2＝0}， B＝{1，2}.
② A＝{长方形}， B＝{平行四边形方形}；
示例3：A＝{1, 2, 7}，B＝{1, 2, 3, 7}，
如果AB，但存在元素x∈B，且x∈A，称A是B的真子集.
示例4：考察下列集合，并指出集合中的元素是什么？A＝{(x, y)| x＋y＝2}；B＝{x| x2＋1＝0，x∈R}.
A表示的是x＋y＝2上的所有的点； B没有元素.
不含任何元素的集合为空集，记作.
规定：空集是任何集合的子集，空集是任何集合的真子集.
例1⑴写出集合{a，b}的所有子集； ⑵写出所有{a，b，c}的所有子集； ⑶写出所有{a，b，c，d}的所有子集.
⑴{a}，{b}，{a，b}，；
⑵{a}，{b}，{c}，{a，b}，{a，b，c}， {a，c}，{b， c}，；
⑶{a}，{b}，{c}，{d}，{a, b}，{b, c}， {a, d}，{a, c}， {b, d}， {c, d}， {a，b，c}，{a，b，d}， {b，c，d}， {a，d，c} {a，b，c，d}，.
一般地，集合A含有n个元素，则A的子集共有2n个，A的真子集共有2n－1个.
A.3个 B.4个 C.5个 D.6个
例3 设集合A＝{1, a, b}， B＝{a, a2, ab}， 若A＝B，求实数a，b.
例4 已知A＝{x | x2－2x－3＝0}, B＝{x | ax－1＝0}, 若BA, 求实数a的值．