苏科版九年级上册2.7 弧长及扇形的面积教案配套ppt课件

这是一份苏科版九年级上册2.7 弧长及扇形的面积教案配套ppt课件，共22页。PPT课件主要包含了2圆的面积公式，C2πR，SπR2，解∵圆心角900，则铁轨长是，问题情景，弧长公式，练一练，扇形的定义，小试牛刀等内容，欢迎下载使用。
(1) 圆的周长公式:
∴铁轨长度是圆周长的
如图,是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗?
为什么是 ？
答：这段铁轨长度是50π米。
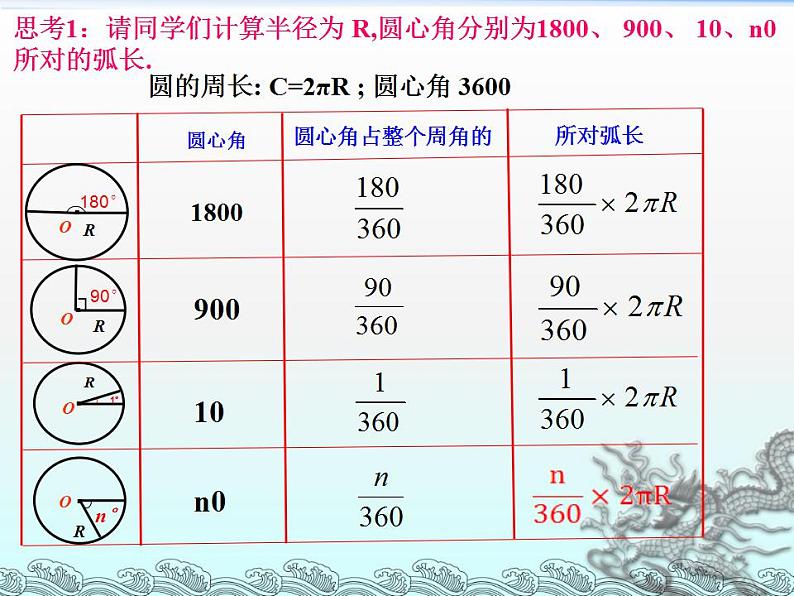
思考1：请同学们计算半径为 R,圆心角分别为1800、 900、 10、n0 所对的弧长.
圆的周长: C=2πR ; 圆心角 3600
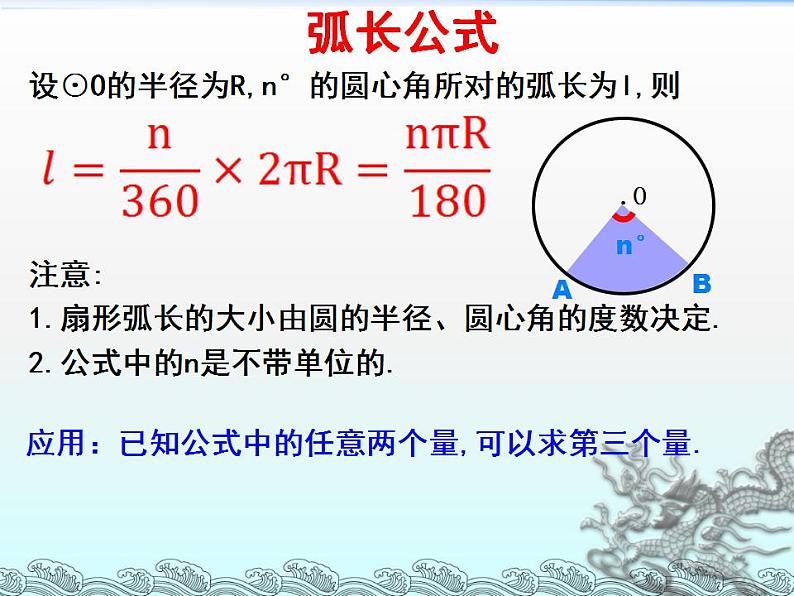
设⊙O的半径为R,n°的圆心角所对的弧长为l,则
注意:1.扇形弧长的大小由圆的半径、圆心角的度数决定.2.公式中的n是不带单位的.
应用：已知公式中的任意两个量,可以求第三个量.
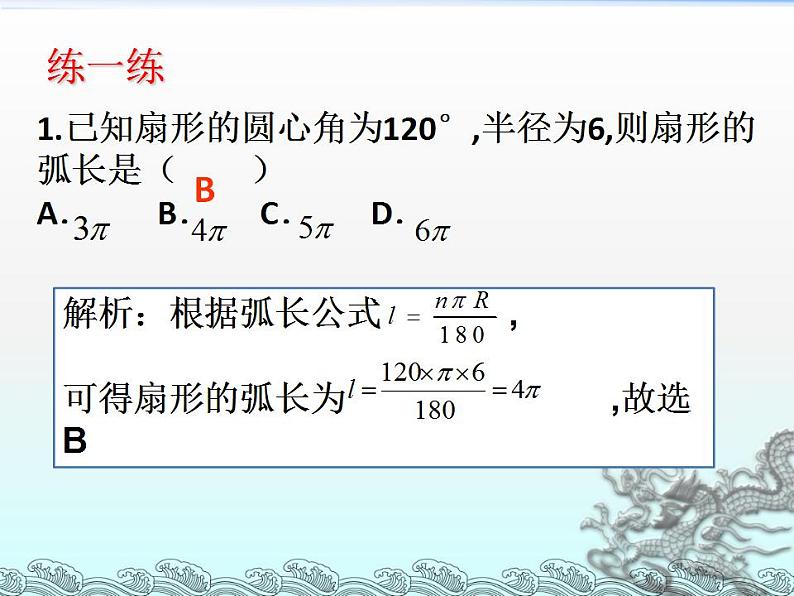
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是（ ）A． B． C． D．
解析：根据弧长公式 ,可得扇形的弧长为 ,故选B
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角是为(　　)A．200° B．160° C．120° D．80°
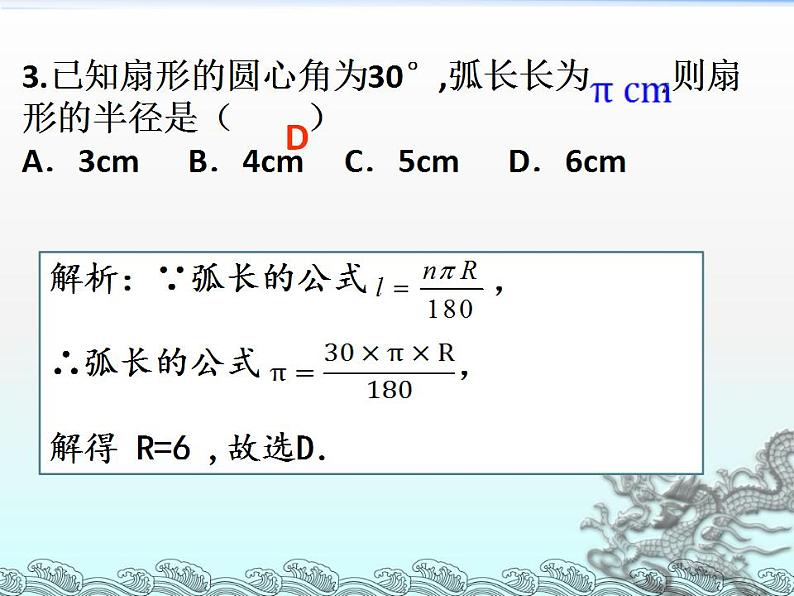
3.已知扇形的圆心角为30°,弧长长为 ,则扇形的半径是（ ）A．3cm B．4cm C．5cm D．6cm
解析：∵弧长的公式 ，∴弧长的公式 ，解得 R=6 ,故选D．
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数).
解：由弧长公式，可得 的长
因此所要求的展直长度
答：管道的展直长度为2970mm．
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
扇形的周长：两条半径和弧长.
思考2：请同学们计算半径为 R,圆心角分别为1800、 900、 10、n0 所对的扇形面积.
圆的面积: S=πR2；圆心角 3600
设⊙O半径为R,圆心角为n°的扇形的面积S扇形，则
注意:1.扇形面积的大小由圆的半径、圆心角的度数决定.2.公式中的n是不带单位的.
思考3：扇形的面积公式与弧长公式有联系吗？
如果扇形的半径为R的圆中,圆心角为n ,那么扇形面积的计算公式为：
扇形的弧长与扇形面积的关系为：
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积S（结果保留小数点后两位）.
S弓形= S扇形OAB-S△OAB
解：连接OA、OB，过圆心O作弦AB的垂直平分线，垂足为D，交 于点C. ∵OC=0.6，DC=0.3 ∴OD=OC-DC=0.3在Rt△OAD中，OA=0.6，OD=0.3∴∠ OAD=30°, , AB=2AD=0.6 ∴∠A OD=60°, ∠ AOB=120°
答：截面上有水部分的面积为
如图,水平放置的圆柱形排水管道的截面半径是2,其中水面高3,求截面上有水部分的面积.
S弓形= S扇形+S△
注意：①当弓形面积小于半圆时S弓形= S扇形-S△②当弓形面积大于半圆时S弓形= S扇形+S△
（07年山东）如图,⊙A、⊙B、⊙C、⊙D两两不相交,且半径都是2,求图中阴影部分的面积.
答：图中阴影部分的面积为12π
拓展：如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC与B点,若OA=6,求 的长.
在Rt△AOC中，∠C=150，∴∠OAB=900-∠C=750
由弧长公式，可得 的长