初中北师大版3 垂径定理说课ppt课件

这是一份初中北师大版3 垂径定理说课ppt课件，共33页。PPT课件主要包含了想一想，归纳总结，做一做等内容，欢迎下载使用。

1．利用圆的轴对称性研究垂径定理及其逆定理；2．运用垂径定理及其逆定理解决问题．
利用圆的轴对称性研究垂径定理及其逆定理．
垂径定理及其逆定理的证明，以及应用时如何添加辅助线．
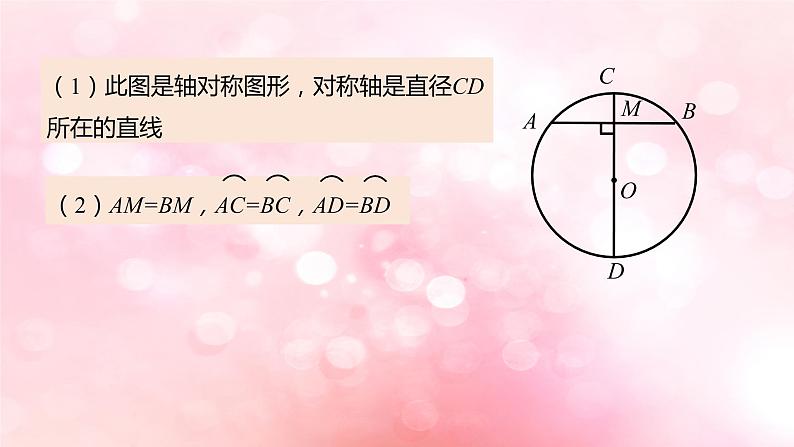
如图,AB是⊙O的一条弦，作直径CD，使CD丄AB，垂足为M.（1）图是轴对称图形吗？如果是，其对称轴是什么？（2）你能发现图中有哪些等量关系？说一说你的理由.
（1）此图是轴对称图形，对称轴是直径CD所在的直线
证明：连接OA、OB、CA、CB，则OA=OB.
即△AOB是等腰三角形.
∴AM=BM，∠AOC=∠BOC.
从而∠AOD=∠BOD.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
∵ CD是直径，CD⊥AB，(条件)
∴ AM=BM，AC =BC,AD =BD.(结论)
下列图形是否具备垂径定理的条件？如果不是，请说明为什么？
不是，因为CD没有过圆心
垂径定理的几个基本图形：
如图所示，在⊙ O 中，AB 为⊙ O 的弦，C，D 是直线AB 上两点，且AC=BD.求证：△ OCD 为等腰三角形.
构建垂径定理的基本图形结合线段垂直平分线性质证明.
解：过点O 作OM ⊥ AB，垂足为M，∵ OM ⊥ AB，∴ AM=BM.∵ AC=BD，∴ CM=DM.又∵ OM ⊥ CD，∴ OC=OD.∴△ OCD 为等腰三角形.
证明：作直径MN⊥AB.∵AB∥CD，∴MN⊥CD.则AM＝BM，CM＝DM（垂直弦的直径平分弦所对的弧） AM－CM＝BM－DM∴AC＝BD
是，对称轴是直径CD所在的直线
如图, AB是⊙O的弦（不是直径），作一条平分AB的直径CD， 交AB于点M.（1）图是轴对称图形吗？如果是，其对称轴是什么？（2）你能发现图中有哪些等量关系？说一说你的理由.
（2）由垂径定理可得AC =BC，AD =BD.
解：（1）连接AO,BO,则AO=BO,
又AM=BM，∴△AOM≌△BOM（SSS），
∴∠AMO=∠BMO=90°，
平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧.
∵ CD是直径，AM=BM，(条件)
∴ AB⊥CD，AC =BC，AD =BD.(结论)
思考：“不是直径”这个条件能去掉吗？如果不能，请举出反例.
特别说明：圆的两条直径是互相平分的.
（1）一条直线过圆心（2）这条直线垂直于弦（3）这条直线平分不是直径的弦（4）这条直线平分不是直径的弦所对的优弧（5）这条直线平分不是直径的弦所对的劣弧
例3 如图所示，AB，CD 是⊙ O 的弦，M，N 分别为AB，CD的中点，且∠ AMN = ∠ CNM. 求证：AB=CD.
解：连接OM，ON，OA，OC.∵ O 为圆心，且M，N 分别为AB，CD 的中点，∴ AB=2AM，CD=2CN，OM ⊥ AB，ON ⊥ CD.∴∠ OMA= ∠ ONC=90° .∵∠ AMN= ∠ CNM，∴∠ OMN= ∠ ONM. ∴ OM=ON.又∵ OA=OC，∴ Rt △ OAM ≌ Rt △ OCN（HL）.∴ AM=CN. ∴ AB=CD
例4 你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m，你能求出赵州桥主桥拱的半径吗？
解：如图，用AB表示主桥拱，设AB所在圆的圆心为O，半径为R.
经过圆心O作弦AB的垂线OC垂足为D，与弧AB交于点C，则D是AB的中点，C是弧AB的中点，CD就是拱高.
∴ AB=37m，CD=7.23m.
解得R≈27.3（m）.
即主桥拱半径约为27.3m.
R2=18.52+(R-7.23)2
设这段弯路的半径为Rm,则OF=(R-90)m.
∴这段弯路的半径约为545m.
如图1、2,一弓形弦长为 　 cm，弓形所在的圆的半径为7cm，则弓形的高为＿＿＿____＿.
2cm或12cm
在圆中有关弦长a,半径r, 弦心距d（圆心到弦的距离），弓形高h的计算题，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a，弦心距d，弓形高h，半径r之间有以下关系：
d+h=r
1.下列说法中,不正确的是(　　)A.圆既是轴对称图形,又是中心对称图形B.圆绕着它的圆心旋转任意角度,都会与自身重合C.圆的对称轴有无数条,对称中心只有一个D.圆的每一条直径都是它的对称轴
3. 如图，⊙O的直径CD＝10 cm，AB是⊙O的弦，AM＝BM，OM∶OC＝3∶5，则AB的长为(　　)A．8 cm　　 cm　　C．6 cm　　D．2 cm
4.如图，AB是⊙O的弦，AB的长为8，P是⊙O上一个动点(不与点A，B重合)，过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为___
5.如图，⊙O的弦AB＝8cm ，直径CE⊥AB于D，DC＝2cm，求半径OC的长.
解：连接OA，∵ CE⊥AB于D，
设OC=xcm，则OD=x-2,根据勾股定理，得
即半径OC的长为5cm.
理由：过O作OE⊥AB，垂足为E， 则AE＝BE，CE＝DE。 ∴ AE－CE＝BE－DE 即 AC＝BD.