










初中数学北师大版九年级下册3 垂径定理说课课件ppt
展开1.进一步认识圆,了解圆是轴对称图形.2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)3.灵活运用垂径定理解决有关圆的问题.(难点)
等腰三角形是轴对称图形吗?如果将一等腰三角形沿底边上的高对折,可以发现什么结论?如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。 (1)该图是轴对称图形吗?如果是,其对称轴是什么? (2)你能图中有哪些等量关系?说一说你的理由。
连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时, 点A与点B重合,
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
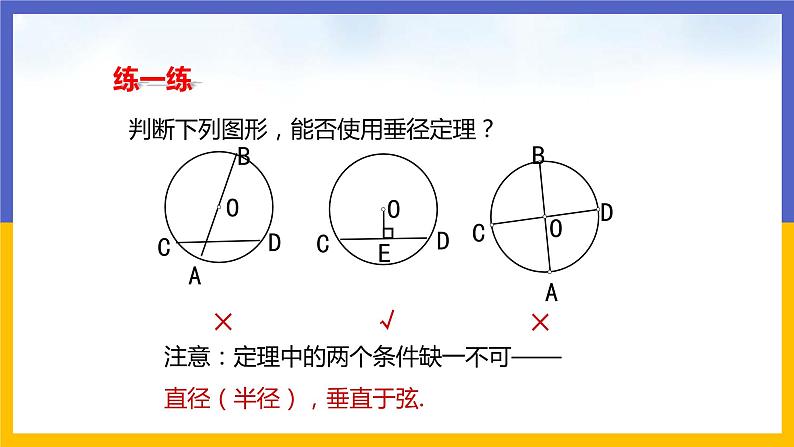
判断下列图形,能否使用垂径定理?
注意:定理中的两个条件缺一不可——直径(半径),垂直于弦.
如图,AB是⊙O 的弦(不是直径),作一条平分AB的直径CD,交AB于点M.(1)下图是轴对称图形吗?如果是,其对称轴是什么? (2)图中有哪些等量关系?说一说你的理由.
由 ① CD是直径
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.思考 如果该定理少了“不是直径”,是否也能成立?
解这个方程,得R=545.
连接OC,设弯路的半径为Rm,则OF=(R-90)m。
根据勾股定理,得 OC²=CF² +OF²
即 R²=300²+(R-90)².
所以,这段弯路的半径为545m.
1、1400年前,我国隋朝建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦长)为37.4米,拱高(即弧的中点到弦的距离)为7.2米,求桥拱所在圆的半径。(结果精确到0.1米)。
2、如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
有三种情况:1、圆心在平行弦外; 2、圆心在其中一条弦上; 3、圆心在平行弦内.
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
两条辅助线:连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
数学七年级上册3.3 整式精品ppt课件: 这是一份数学七年级上册3.3 整式精品ppt课件,文件包含3整式pptx、3整式doc等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
北师大版九年级下册3 垂径定理完美版习题ppt课件: 这是一份北师大版九年级下册3 垂径定理完美版习题ppt课件,文件包含33垂径定理课件pptx、33垂径定理教案doc、第三章圆2圆的对称性习题33课件pptx等3份课件配套教学资源,其中PPT共33页, 欢迎下载使用。
初中数学北师大版八年级下册3 中心对称获奖课件ppt: 这是一份初中数学北师大版八年级下册3 中心对称获奖课件ppt,文件包含33中心对称pptx、北师大版数学八年级下册第三章图形的平移与旋转33中心对称教学详案docx、33中心对称同步练习docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。














