北师大版九年级下册3 垂径定理精品ppt课件

北师大版数学九年级下《3.3垂径定理》学案

学习目标：1.理解圆的轴对称性、垂径定理及其逆定理，并会运用其解决有关问题．

2.通过学习垂径定理及其逆定理的证明，培养类比分析、猜想探索的能力．

3.在学习过程中让学生感受几何图形的对称美．进一步体会和理解研究几何图形的各种方法．

学习重点：运用探索、推理，充分把握圆中的垂径定理及其逆定理

学习难点：运用垂径定理及其逆定理进行有关的计算和证明

学习过程：

一、新知导入

1.圆是轴对称图形吗？

2.它的对称轴是什么?

3.你能找到多少条对称轴？

二、新知探究

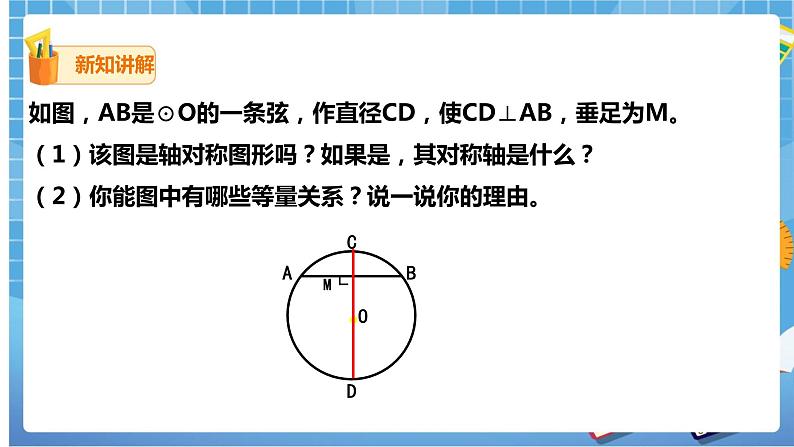
1．如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为M．

（1）该图是轴对称图形吗？如果是，其对称轴是什么？

（2）你能图中有哪些等量关系？说一说你的理由．

2．垂径定理的内容：______________________________________________

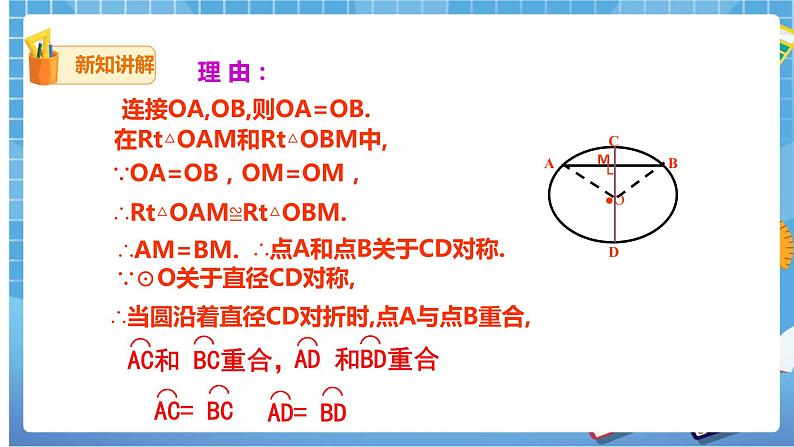
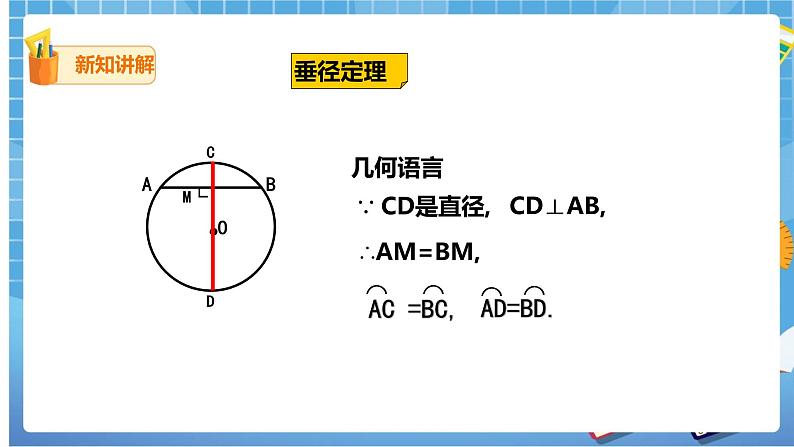
几何语言:

∵ CD是直径,

∴_____________、________________、________________

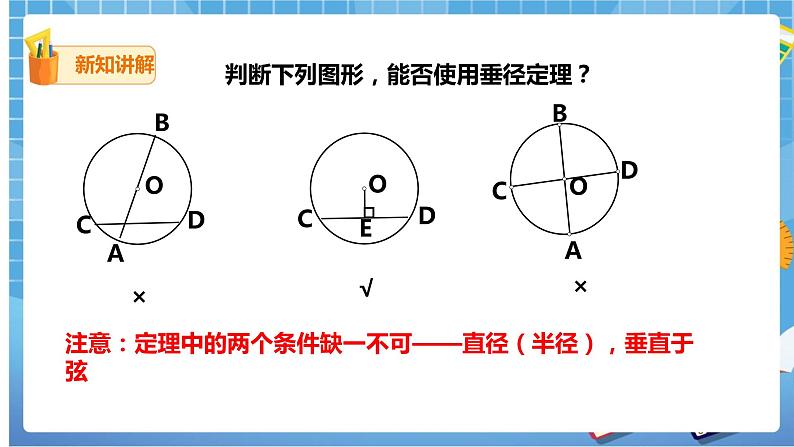
3．辨析：判断下列图形，能否使用垂径定理？

注意：定理中的两个条件缺一不可——直径（半径），垂直于弦．

4．垂径定理逆定理的探索

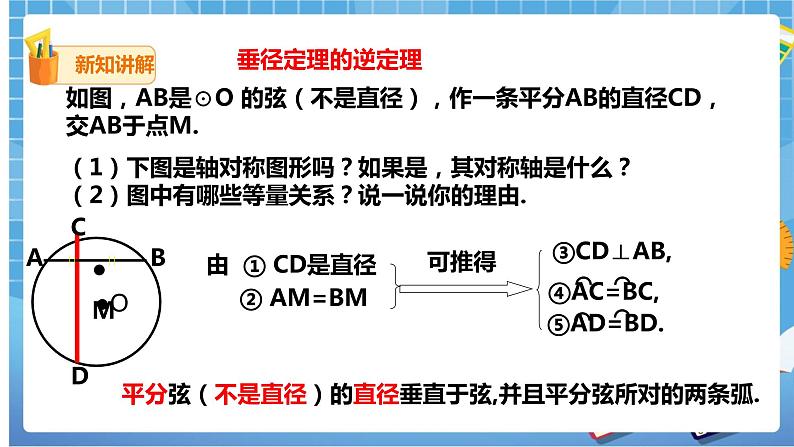
如图，AB是⊙O 的弦（不是直径），作一条平分AB的直径CD，交AB于点M.

（1）下图是轴对称图形吗？如果是，其对称轴是什么？

（2）图中有哪些等量关系？说一说你的理由.

垂径定理的逆定理: 平分弦（不是直径）的直径________________________________

5．辨析：“平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧．”如果该定理少了“不是直径”，是否也能成立？

三、课堂练习

1．如图，一条公路的转弯处是一段圆弧（即图中,点0是所在圆的圆心），其中CD=600m，E为上的一点，且OE⊥CD，垂足为F，EF=90m.求这段弯路的半径．

2.如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知CD = 20，CM = 4，求AB.

四、拓展提高

1.我是赵州桥，我历史悠久，是世界上现存最早、保存最好的巨大石拱桥。我的主桥是圆弧形,我的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m，但一千多年了，我还不知道我主桥拱的半径是多少，你能帮我算算吗？

2.已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。你认为AC和BD有什么关系？为什么？

五、学习小结

活动内容：通过这节课的学习，你有哪些收获？有何感想？学会了哪些方法？先想一想，再分享给大家．

六、作业布置:

1.教材76页练习第3题    2.  习题3.3

七、自我检测:

1．如图，已知⊙O的半径为13，弦AB长为24，则点O到AB的距离是（　　）

A. 6        B. 5            C. 4          D. 3

（第1题图）             （第2题图）           （第3题图）

2．如图，⊙O的直径CD垂直弦AB于点E，且CE＝2，DE＝8，则AB的长为(　　)

A. 2        B. 4             C. 6        D. 8

3．如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON＝(   )

A. 5         B. 7            C. 9         D. 11

4．如图，在半径为5的⊙O中，弦AB=6，OP⊥AB，垂足为点P，则OP的长为（  ）.

A．3          B．2.5        C．4         D．3.5

（第4题图）             （第5题图）           （第6题图）

5．如图，⊙O过点B、C，圆心O在等腰直角△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为(　     　)

A.         B. 2          C.             D. 3

6．如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（  ）

A. AE＝OE     B. CE＝DE     C. OE＝CE        D. ∠AOC＝60°

7．已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC的长为（　　）

A. 2cm      B. 4 cm     C. 2cm或4cm     D. 2cm或4cm

8．已知⊙O的半径为15，弦AB的长为18，点P在弦AB上且OP=13，则AP的长为（　　）

A. 4             B. 14           C. 4或14            D. 6或14

二、填空题

9． 如图，AB是⊙O的直径，CD为弦，CD⊥AB于E，若CD=6，BE=1，则⊙O的直径为        ．

（第9题图）             （第10题图）           （第11题图）

10．如图，在⊙O中，弦AB=6，圆心O到AB的距离OC=2，则⊙O的半径长为______．

11．如图，AB是⊙O的直径，CD为⊙O的一条弦，CD⊥AB于点E，已知CD=4，AE=1，则⊙O的半径为______．

12．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，则BE=______．

三、解答题

13．已知：如图，AB是⊙O的直径，CD是⊙O的弦， 且AB⊥CD，垂足为E，联结OC， OC=5，CD=8，求BE的长．

14．已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C、D(如图)．

(1)求证：AC＝BD；

(2)若大圆的半径R＝10，小圆的半径r＝8，且圆O到直线AB的距离为6，求AC的长．

自我检测参考答案

1．B

【解析】试题分析：过O作OC⊥AB于C，根据垂径定理求出AC=BC=AB=12，在Rt△AOC中，由勾股定理得：OC==5．

故选：B．

考点：1、垂径定理；2、勾股定理

故选A.

点睛：垂直于弦的直径平分弦，并且平分弦所对的两条弧.

4．C．

【解析】

试题分析：连接OA，根据垂径定理得到AP=AB=×6=3，利用勾股定理得OP==4.

故选：C．

考点：垂径定理；勾股定理．

5．C

【解析】试题分析：过A作AD⊥BC，由题意可知AD必过点O，连接OB，∵△BAC是等腰直角三角形，AD⊥BC，∴BD=CD=AD=3，∴OD=AD﹣OA=2，Rt△OBD中，根据勾股定理，得：OB==．故选C．

【解析】连接AC，AO，

∵O的直径CD=10cm，AB⊥CD，AB=8cm，

∴AM=AB=×8=4cm,OD=OC=5cm,

当C点位置如图1所示时，

∵OA=5cm，AM=4cm，CD⊥AB，

∴OM==3cm，

∴CM=OC+OM=5+3=8cm，

∴AC=cm；

当C点位置如图2所示时，同理可得OM=3cm，

∵OC=5cm，

∴MC=5−3=2cm，

在Rt△AMC中,AC=cm.

故选C.

8．C

【解析】试题解析：如图：

作于点C，

OC= =12，又

∴PC==5，

当点P在线段AC上时，  

当点P在线段BC上时，  

故选C．

9．10．

【解析】

试题分析：如图，，∵AB是⊙O的直径，而且CD⊥AB于E，∴DE=CE=12÷2=6，在Rt△ODE中，，解得x=5，∵5×2=10，∴⊙O的直径为10．故答案为：10．

考点：垂径定理．

10．

【解析】试题分析：根据垂径定理求出AC，根据勾股定理求出OA即可． ∵弦AB=6，圆心O到AB的距离OC为2， ∴AC=BC=3，∠ACO=90°， 由勾股定理得：OA=

考点：垂径定理．

11．

【解析】试题分析：连接OC，则OC=r，OE=r－1，CE=CD=2，根据Rt△OCE的勾股定理可得：，解得：r=．

考点：垂径定理．

12．4-

【解析】试题分析：如图，连接OC．∵弦CD⊥AB于点E，CD=6，∴CE=ED=CD=3．∵在Rt△OEC中，∠OEC=90°，CE=3，OC=4，∴OE==，∴BE=OB﹣OE=．故答案为：．

考点：垂径定理；勾股定理．

【解析】试题分析：（1）过O作OE⊥AB，根据垂径定理得到AE=BE，CE=DE，从而得到AC=BD；

（2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，再根据勾股定理求出CE及AE的长，根据AC=AE﹣CE即可得出结论．

试题解析：（1）作OE⊥AB，

∵AE=BE，CE=DE，

∴BE﹣DE=AE﹣CE，即AC=BD；

（2）∵由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，∴OE=6，

∴CE=，

AE=，

∴AC=AE﹣CE=8﹣2．

考点：1、垂径定理，2、勾股定理