

必修13.1.2 指数函数教学设计
展开3.3《指数函数及其性质》(第一课时)
一、 教学目标:
1.知识与技能
①通过实际问题了解指数函数的实际背景;
②理解指数函数的概念和意义,根据图象理解和掌握指数函数的性质;
③体会具体到一般数学讨论方式及数形结合的思想.
2.情感、态度、价值观
①让学生了解数学来自生活,数学又服务于生活的哲理.
②培养学生观察问题,分析问题的能力.
3.过程与方法
展示函数图象,让学生通过观察,进而研究指数函数的性质.
二、重、难点
重点:指数函数的概念和性质及其应用.
难点:指数函数性质的归纳,概括及其应用.
三、学法与教具:
①学法:观察法、讲授法及讨论法.
②教具:多媒体.
四、教学过程
(一)情境设置
问题1:将一张纸对折再对折依次下去,所得到纸的层数与对折次数的函数关系式是_______.
问题2:《庄子·逍遥游》记载:一尺之椎,日取其半,万世不竭. 意思是一尺长的木棒,一天截取一半,很长时间也截取不完. 这样的一个木棒截取次,剩余长度与截取次数的函数关系式是_______.
引导学生观察,,,两个函数中,底数是常数,指数是自变量.
(二)讲授新课
指数函数的定义:
一般地,函数(>0且≠1)叫做指数函数,其中是自变量,函数的定义域为R.
想一想:指数函数定义中,为什么规定“”如果不这样规定会出现什么情况?
(1)若a<0会有什么问题?(如则在实数范围内相应的函数值不存在)
(2)若a=0会有什么问题?( )
(3)若 a=1又会怎么样?(1x无论x取何值,它总是1,对它没有研究的必要.)
师:为了避免上述各种情况的发生,所以规定且 .
例1:在下列的关系式中,哪些不是指数函数,为什么?
(1) (2) (3)
(4) (5) (6)
例2 已知指数函数(且 )的图象经过点,求的值.
我们在学习函数的单调性的时候,主要是根据函数的图象,即用数形结合的方法来研究. 下面我们通过动手试一试来探究指数函数的相关性质。
(三)动手试一试
同学们分组画出下列函数的图象:
(1)与的图象;
(2)与的图象;
完成以下表格并绘出函数的图象
|
| 1 |
| 2 |
| 4 |
完成以下表格并绘出函数的图象.
|
| 1 |
| 2 |
| 4 |
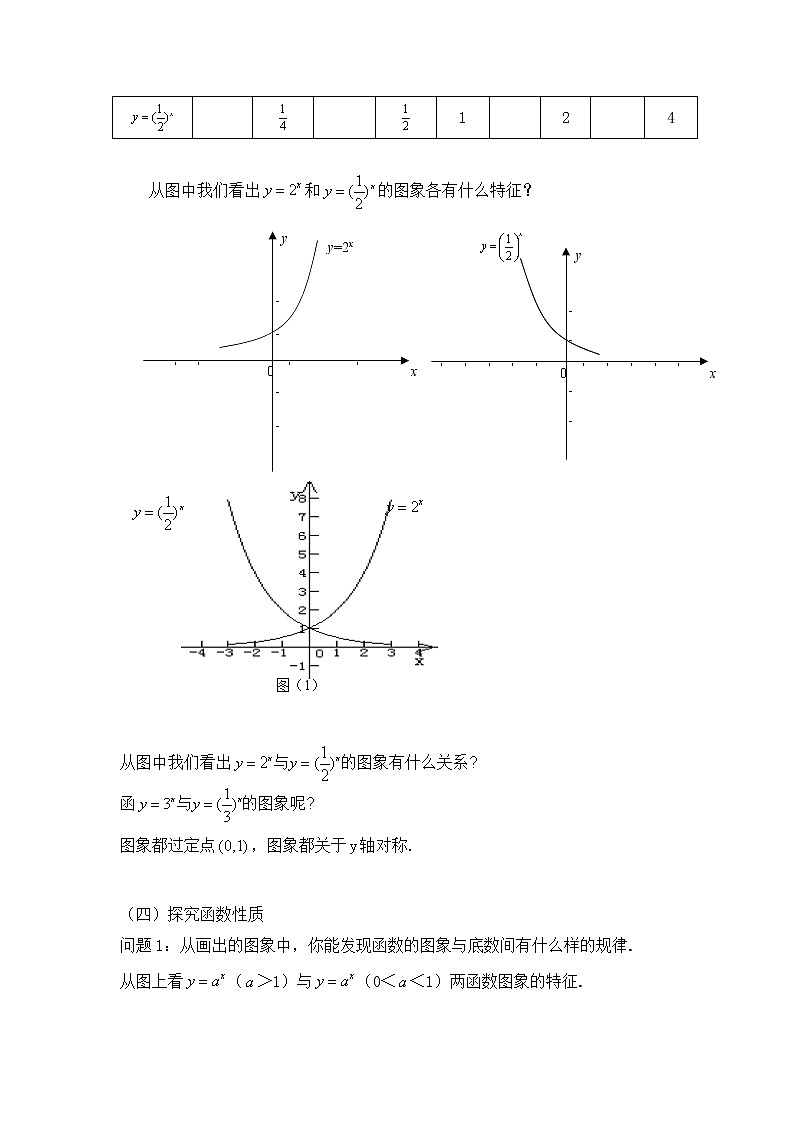
从图中我们看出和的图象各有什么特征?
从图中我们看出
函
图象都过定点,图象都关于轴对称.
(四)探究函数性质
问题1:从画出的图象中,你能发现函数的图象与底数间有什么样的规律.
从图上看(>1)与(0<<1)两函数图象的特征.
问题2:根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
问题3:指数函数(>0且≠1),当底数越大时,函数图象间有什么样的关系.
| ||
图象 | ||
性质 | (1)定义域: | |
(2)值域: | ||
(3)过点,即时 | ||
(4)在上是增函数 | (4)在上是减函数 | |
(五)质疑答辩,排难解惑,发展思维。
例3 比较下列各题中两个值的大小:
(1),; (2),; (3),.
课堂练习:
1、下列函数中一定是指数函数的是________.
①;②;③;④;⑤;⑥.
2、若指数函数是上的单调减函数,那么实数的取值范围是_______.
3、指出下列函数的单调性:
(1);(2);(3);(4).
4、比较下列各组数中两个值的大小关系:
(1),; (2),;(3),;
(4),;(5),;(6),.
(三)归纳小结
1、指数函数的概念及图象和性质
2、要求出指数函数,需要几个条件?
(四)教学反思:
1、理解指数函数
2、解题利用指数函数的图象,可有利于清晰地分析题目,培养数型结合与分类讨论的数学思想 .
(五)课后练习:
1、某种细胞分裂时,由个分裂成个,个分裂成个,…依次类推,写出一个这样的细胞分裂次后,得到的细胞个数与分裂次数之间的函数关系式.
2、用清水漂洗衣服,已知每次能洗去污垢的,设漂洗前衣服上的污垢量为,写出衣服上存留的污垢量与漂洗次数之间的函数关系式. 若要使存留的污垢不超过原有的%,则至少要漂洗几次?
3、比较下列各组数中两个值的大小:
(1),;(2),;(3),;
(4),.
4、分别把下列各题中的个数按从小到大的顺序用不等号连接起来:
(1),,; (2),,;
(3),,; (3),,.
苏教版必修13.1.2 指数函数教学设计: 这是一份苏教版必修13.1.2 指数函数教学设计,共4页。教案主要包含了设计意图等内容,欢迎下载使用。
高中数学苏教版必修13.1.2 指数函数教案及反思: 这是一份高中数学苏教版必修13.1.2 指数函数教案及反思,共4页。教案主要包含了课题,教学目标,教学重点与难点,教学方法与手段,教学过程,布置作业等内容,欢迎下载使用。
苏教版必修13.1.2 指数函数教案设计: 这是一份苏教版必修13.1.2 指数函数教案设计,共7页。教案主要包含了复习回顾,新课引入,师生互动,新课讲解,抽象特征,建构概念等内容,欢迎下载使用。













