数学必修13.1.2 指数函数教学设计
展开指数函数
得分
阅卷人
一、选择题(共29题,题分合计145分)
1.指数函数y=f(x)的反函数的图象过点(2,-1),则此指数函数为
A. B. C. D.
2.下列f(x)=(1+ax)2是
A.奇函数 B.偶函数 C.非奇非偶函数 D.既奇且偶函数
3.函数y=的反函数是
A.奇函数且在(0,+∞)上是减函数 B.偶函数且在(0,+∞)上是减函数
C.奇函数且在(0,+∞)上是增函数 D.偶函数且在(0,+∞)上是增函数
4.若函数y=3+2x-1的反函数的图像经过P点,则P点坐标是
A.(2,5) B.(1,3) C.(5,2) D.(3,1)
5.已知0
6.如图,当时,函数和的图象只可能是
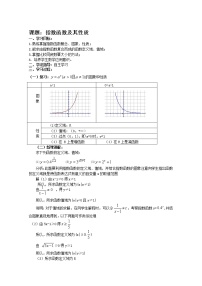
7.图中的曲线是指数函数的图象,已知a的值分别取,,,,则相应于曲线C1,C2,C3,C4的a依次为
8.已知函数是定义域上的减函数,则字母a的取值范围是
A.0<a<1 B. C.-1<a<1 D.-1<a<0
9.已知三个数M=0.32-0.32,P=0.32-3.2,Q=3.2-0.32,则它们的大小顺序是
A.M<P<Q B.Q<M<P C.P<Q<M D.P<M<Q
10.如果a,b,c都是小于1的正数,且x∈(-∞,0),ax<bx<cx,则
A.a<b<c B.c<a<b C.b<c<a D.c<b<a
11.已知f (x)是偶函数,且x>0时,时,则x<0时,f (x)等于
A.10x B.10-x C.-10x D.-10-x
12.若指数函数在[-1,1]上的最大值与最小值的差是1,则底数a等于
A. B. C. D.
13.下列函数中,值域是(0,+∞)的是
A.y= B.y=2x+3 x∈(0,+∞)
C.y=x2+x+1 D.y=
14.当x∈[0,+¥]时,下列函数中不是增函数的是
A.y=x+a2x-3 B.y=2x C.y=2x2+x+1 D.y=|3- x|
15.已知p>q>1,0
16.若-1
17.函数y=(a2-1)-x与它的反函数在(0,+¥)上都是增函数,则a的取值范围是
A.1<|a|< B. |a|<且|a|≠1
C.|a|> D. |a|>1
18.函数f(x)=(a2-1)x在R上是减函数,则a的取值范围是
A. B. C.a< D.1<
19.一批设备价值a万元,由于使用磨损,每年比上一年价值降低b%,则n年后这批设备的价值为
A.na(1-b%) B.a(1-nb%) C.a[(1-(b%))]n D.a(1-b%)n
20.如果且,则下列不等式中正确的是
A. B. C. D.
21.下列四个命题中,真命题的是
A.y=2x+1和都是指数函数 B.指数函数y=ax的最小值是0
C.对任意的,都有3x>2x D.函数y=ax与的图象关于y轴对称
22.要得到函数的图象,只需将指数函数的图象
A.向左平行移动1个单位 B.向右平行移动1个单位
C.向左平行移动个单位 D.向右平行移动个单位
23.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为2个),经过3个小时,这种细菌由1个可繁殖成
A.511个 B.512个 C.1023个 D.1024个
24.函数y=2x与y=x2的图象的交点个数是
A.0个 B.1个 C.2个 D.3个
25.设指数函数f (x) = ax(a>0,a≠1),则下列等式中不正确的是
A. f(x+y)=f(x)·f(y)
26.若函数在上为减函数,则a满足
A. B. C. D.
27.已知镭经过100年剩留原头质量的95.76%,设质量为1的镭经过x年后的剩留量为y,则x, y之间的函数关系是
A. B. C. D.
28.四个函数
A.定义域都是R B.图象都不在x轴下方
C.在(0,+¥)上都是增函数 D.图象都过点(0,1)
29.函数f(x)的图像与函数g(x)=()x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为
A.(0,1) B.[1,+) C.(-,1] D.[1,2)
得分
阅卷人
二、填空题(共18题,题分合计71分)
1.函数y=3的单调递减区间是 .
2.将三个数按从小到大的顺序排列_________________________.
3.当a>0且a≠1时,函数f(x)=ax-2-3必过定点 .
4.函数y=3的定义域是 ,值域是 .
5.函数y=a(0<a<1)的定义域是 ,单调递增区间是 .
6.若a
8.直线x=a(a>0)与函数y=()x,y=()x,y=2x,y=10x的图像依次交于A、B、C、D四点,则这四点从上到下的排列次序是 .
9.若f(52x-1)=x-2,则f(125)= .
10.已知f(x)=2x,g(x)是一次函数,记F(x)=f[g(x)],并且点(2,)既在函数F(x)的图像上,又在F-1(x)的图像上,则F(x)的解析式为 .
11.函数的定义域是 , 值域是 .
12.若函数的图象不经过第二象限,则m的取值范围是_________.
13.已知-1
15.若点既在函数的图象上, 又在它的反函数的图象上,则a= b= .
16.已知函数f(x)的图象关于y轴对称,函数g(x)的图象关于原点对称,且f(x)+ g(x)=10x 则f (x)= g (x)= ______ .
17.函数y=m2x+2mx-1(m>0且m1),在区间[-1,1]上的最大值是14,则m的值是 .
18.满足的正数x的取值范围是 .
得分
阅卷人
三、解答题(共40题,题分合计440分)
1.求函数的定义域及值域.
2.求函数的反函数.
3.0
4.若函数y=4x-3·2x+3的值域为[1,7],试确定x的取值范围.
5.讨论函数的增减性.
6.解方程:
(1)
(2)
(3)
7.说明指数函数的图象经过怎样的变换,可以得到函数的图象,并画出它们的图象.
8.(1)判断函数和(其中)的奇偶性;
(2)证明指数函数可以表示为一个偶函数与一个奇函数的和.
9.一种产品的成本原来是1万元,近几年来,由于大搞技术创新,降低了能耗,使得该产品的成本每年平均比上一年降低11%,试画出成本随时间变化的函数图象,并从图上求出多少年后,该产品成本降为原来的一半以下.
10.设函数
(1)画出函数的图象;
(2)根据图象指出函数的单调区间.
11.已知n∈N*,f (n)= n·0.9 n,比较f (n)与f (n+1)的大小,并求f (n)的最大值.
12.已知气压与高度的指数函数成比例,越往高处气压越低,以至接近于0。如果海平面的气压为1000百帕(百帕是气压单位),在海拔3000米山顶的气压为700百帕,问高出海平面12000米的飞机在多少百帕的气压中飞行?(精确到0.1百帕)
13.已知在(0,+∞)上是增函数,求m的取值范围.
14.求函数y=a的值域和单调区间.
15.a元人民币存入银行,银行每年支付p%的年利息,然后每年再将利息计入存款之内,求m年后的存款总额.
16.比较下列各组数的大小:
(1)aabb与aabb(a>b>0);
(2)1.7,1.7,0.7
17.判断的奇偶性.
18.画出函数y=|2x-1|的图象,并由图象写出函数的单调区间.
19.已知
(1)求反函数的定义域;
(2)求.
20.设a∈R,f(x)= (x∈R),试确定a的值,使f(x)为奇函数.
21.求函数的定义域及单调递增区间.
22.求函数的定义域.
23.求函数的定义域及值域.
24.若关于x的方程,有实根,试考虑a的取值范围.
25.作出下列函数的图象,并由图象指出:①函数的单调区间;②当x取什么值时,函数有最值.
(1)y=2|x-2|;
(2)y=|2x-2|
26.已知函数(a>1)
(1)判断函数f(x)的奇偶性;
(2)求f(x)的值域;
(3)证明f(x)在(-∞,+∞)上是增函数.
27.已知函数
(1)求f(x)的定义域和值域;
(2)判断f(x)的奇偶性;
(3)讨论f(x)的单调性.
28.如果函数y=a2x+2ax-1(a>0且a≠1)在区间[-1,1]上最大值为14,求a的值.
29.已知x+x=3(x>0),求x+x的值.
30.求函数,x∈[-3,2]的单调区间及值域.
31.已知函数f(x)=2x (ax2+bx+c)恒满足关系式f(x+1)-f(x)=2x·x2,求常数a,b,c的值.
32.若,(a>0且a≠1),试用f(x),g(x),f(y),g(y)表示f(x+y).
33.设,其中a∈R,n是任意给定的自然数且n≥2,如果对x∈(-∞,1],恒有f(x)>0,求a的取值范围.
34.求函数的值域和单调区间.
35.设y1= a2x,y2= a x2-3,其中a>0,a ≠1,x为何值时,有
(1)y1=y2; (2)y1
37.已知9x+4y=1,求3x-1+22y -1的最大值.
38.设函数
(1)求证:无论a为何实数, f (x)总是增函数;
(2)确定a值,使f (x)为奇函数;
(3)当f (x)为奇函数时,求f (x)的值域.
39.已知9x+4y=a2,求3x+22y+1的最大值.
40.(1)已知是奇函数,求常数m的值;
(2)画出函数的图象,并利用图象回答:k为何值时,方程|3x-1|=k无解?有一解?有两解?
指数函数答案
一、选择题(共29题,合计145分)
1.1870答案:A
2.2095答案:B
3.2100答案:C
4.2102答案:C
5.2109答案:A
6.2154答案:A
7.2519答案:A
8.2533答案:C
9.2534答案:B
10.2535答案:D
11.2563答案:B
12.2564答案:D
13.4112答案:D
14.4125答案:D
15.4136答案:B
16.4137答案:D
17.4138答案:A
18.2093答案:D
19.2111答案:D
20.2142答案:B
21.2500答案:D
22.2501答案:D
23.2502答案:B
24.2570答案:D
25.2571答案:D
26.1991答案:C
27.2012答案:A
28.2140答案:B
29.4141答案:A
二、填空题(共18题,合计71分)
1.2119答案:(0,+)
2.2498答案:
3.2537答案:(2,-2)
4.2538答案:{x|x2},{y|y>0且y1}
5.2539答案:{x|x2或x0},(-,0]
6.2112答案:0
8.2118答案:D、C、B、A
9.2120答案:0
10.2123答案:2
11.2503答案: ,
12.2504答案:
13.2505答案:
14.2565答案:(0,1)
15.2566答案: ,
16.2573答案: ,
17.2121答案:或3
18.2572答案:
三、解答题(共40题,合计440分)
1.2163答案:定义域为,值域为R
2.2165答案:
3.2124答案:2
5.2158答案:当时,是增函数,当时是减函数
6.2227答案:(1)
(2)x=2
(3)
7.2499答案:将指数函数的图象向右平行移动1个单位,就得到函数的图象;再作出函数的图象关于y轴的对称图形,就得到函数的图象,即函数的图象,最后,将函数的图象向上平行移动2个单位,就得到函数的图象
8.2506答案:f(x)是偶函数
g(x)是奇函数
9.2507答案:6年后,该产品成本降为原来的一半以下
10.2509答案:在上是减函数,在上是增函数
11.2510答案:当1
当n>9时,f(n+1)
12.2520答案:240.1(百帕)
13.2523答案:取值范围是2<m<4或-2<m<0
14.2524答案:值域是(0,a-4],单调递增区间是(-∞,1],单调递减区间是[1,+∞)
15.2540答案:a(1+p%)m
16.2545答案:(1)aabb>abba
(2)1.7>1.7>0.7
17.2546答案:偶函数
18.2547答案:减区间是(-∞,0],增区间为[0,+∞)
19.1970答案:见注释
20.2127答案:a=1
21.2141答案:定义域为
故的单调递增区间为
22.2155答案:
23.2172答案:
24.2508答案:a的取值范围为
25.2522答案:(1)这个函数的递减区间是(-∞,2],递增区间是[2,+∞),且当x=2时,y有最小值1
(2)这函数的递减区间是(-∞,1],递增区间是[1,+∞),当x=1时,y有最小值0
26.2525答案:(1)是奇函数
(2)值域为(-1,1)
27.2551答案:(1)定义域为(-∞,+∞),值域为(-1,1);
(2)奇函数;
(3)f(x)在(-∞,+∞)上单调递增
28.2552答案:
29.2553答案:
30.2558答案:单调递增区间为[1,2],单调递减区间为[-3,1],值域为
31.2559答案:a=1,b=-4,c=6
32.2560答案:f(x+y)=f(x)f(y)+g(x)g(y)
33.2562答案:
34.2567答案:值域是
函数在上是增函数,在上是减函数
35.2569答案:(1)x=-1或x=3
(2)x<-1或x>3
36.2574答案:函数的值域为
函数的单调增区间是,单调减区间是
37.2575答案:
38.1898答案:(1)用单调函数定义,结合指数函数单调性证明
(2)时f (x)是奇函数
(3)f (x)的值域是(-1,1)
39.2557答案:
40.2568答案:(1)常数m=1
(2)当k<0时,直线y=k与函数的图象无交点,即方程无解;
当k=0或k1时,直线y=k与函数的图象有唯一的交点,所以方程有一解;
当0
苏教版必修1第3章 指数函数、对数函数和幂函数3.1 指数函数3.1.2 指数函数教案及反思: 这是一份苏教版必修1第3章 指数函数、对数函数和幂函数3.1 指数函数3.1.2 指数函数教案及反思,共3页。教案主要包含了选择题.,填空题.,解答题等内容,欢迎下载使用。
高中数学苏教版必修13.1.2 指数函数教学设计: 这是一份高中数学苏教版必修13.1.2 指数函数教学设计,共3页。教案主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学苏教版必修13.1.2 指数函数教学设计及反思: 这是一份高中数学苏教版必修13.1.2 指数函数教学设计及反思,共3页。教案主要包含了选择题,填空题,解答题等内容,欢迎下载使用。