高中数学苏教版必修13.4.1 函数与方程教案

这是一份高中数学苏教版必修13.4.1 函数与方程教案，共5页。教案主要包含了目标瞭望台，概念构建，运用，学生练习，课堂小结等内容，欢迎下载使用。

一、目标瞭望台
1．通过具体实例理解二分法的概念及其适用条件，并能够根据这样的过程进行实际求解．了解二分法是求方程近似解的常用方法，从中体会函数与方程之间的联系及其在实际问题中的应用．
2．通过本节内容的学习，让学生体会到在现实世界中，等是相对的，而不等是绝对的，这样可以加深对数学的理解．
一、引入（6分钟）
在一个风雨交加的夜里，从某水库闸房到防洪指挥部的电话线路发生了故障．这是一条10 km长的线路，如何迅速查出故障所在？
如果沿着线路一小段一小段查找，困难很多．每查一个点要爬一次电线杆，10km长，大约有200多根电线杆呢．想一想，维修线路的工人师傅怎样工作最合理？
这样每查一次，就可以把待查线路长度缩减为原来的一半，故经过7次查找，就可以将故障发生的范围缩小到50—100m左右，即在一两根电线杆附近．
这在现实生活中也有许多重要的应用．其思想方法在生活中解答以上这类问题时经常碰到．解答以上这类实际问题关键在于，根据实际情况加以判断和总结，巧妙取中点，巧妙分析和缩小故障的区间，从而以最短的时间和最小的代价达到目的．
二、概念构建
问题1 什么是二分法？
对于区间上连续不断，且的函数，通过不断地
把函数的零点所在区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法．
（有困难可扫描二维码学习微视频《二分法(配套学案定制)》）
问题2 给定精确度，用二分法求函数零点近似值的步骤：
（1）确定，从而确定零点存在的区间；
（2）求区间的中点，并计算；
（3）判断零点范围：若，则就是函数的零点；若，则零点；若，则零点；
（4）判断精确度：若区间两个端点的近似值相同（符合精确度要求），这个近似值即为所求，否则重复(2)～(4)．
三、运用
例1 求方程在区间上的近似解(精确到0.1)．
解：因为,,
所以在区间内,方程有一解,记为.
取和的平均数.因为,所以.
再取与的平均数.因为,所以.
如此继续下去,得
,
因为与精确到的近似值都为,
所以此方程在区间上的近似值为.
（有困难可扫描二维码学习微视频《二分法求零点(配套学案定制)》）
四、学生练习
例2 借助计算器用二分法求方程的近似解(精确到0.1).
解:由题可知，方程的根唯一，且.
记函数．
则,
又则,
又则,
又则,
又则.
因为与精确到的近似值都为,
所以此方程在区间上的近似值为.
（有困难可扫描二维码学习微视频《二分法求函数近似解例2(配套学案定制)》）
x
y
4
0
4
y=2x
y=4－x
1
变式训练：利用计算器求方程的近似解(精确到0.1)．
分析：先利用函数与函数的图象，
估计出方程的解所在的区间.
然后运用二分法求出该方程的近似解.
解:分别画出函数与函数的图象,可知方程的解在区间上.对于区间,利用二分法就可以求得它的近似解为.
（有困难可扫描二维码学习微视频《二分法求零点变式训练(配套学案定制)》）
五、课堂小结
1.二分法是求函数零点近似解的一种计算方法.
2.用二分法求函数零点的一般步骤：
（1）零点存在性定理,求出初始区间；
（2）进行计算,确定下一区间
（3）循环进行,达到精确要求
二分法渗透了极限和算法的思想.
练习
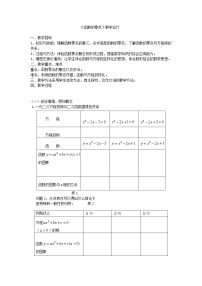
1．确定下列函数的零点与方程的根存在的区间：
（1）函数有零点的区间是 ．
答案
（2）方程正根所在的区间是 ．
答案
（3）方程负根所在的区间是 ．
答案
（4）函数有零点的区间是 ．
答案
2．用二分法求方程在区间内的实根，取区间中点，那么下一个有根区间是 ．
答案
3．求函数零点的近似值 (精确到0.1)．
解：作出函数与的图象，
方程的根应有3个分别在区间内
由二分法可知在区间内的近似解约为－1.9；
在区间内的近似解约为0.4；
在区间内的近似解约为1.5.
（有困难可扫描二维码学习微视频《求函数零点的近似值练习3(配套学案定制)》）