



初中人教版第十四章 整式的乘法与因式分解综合与测试复习ppt课件
展开1.知道因式分解的概念、平方差公式和完全平方公式,会利用提公因式法、公式法分解因式.2.熟悉同底数幂的乘法、幂的乘方、积的乘方单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的法则,能够利用整式乘法的法则进行运算.3.熟悉同底数幂的除法、零指数幂、单项式除以单项式、多项式除以单项式的运算法则,能够利用整式的除法法则进行运算.4.学会类比和转化思想,并能够运用方程思想、整体思想解决问题.
重点:运用整式的乘法法则和除法法则进行运算;因式分解.难点:应用整式的乘法和因式分解决问题.
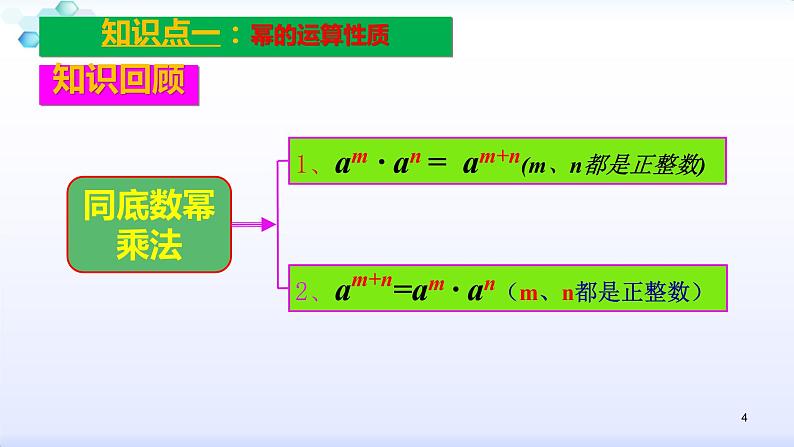
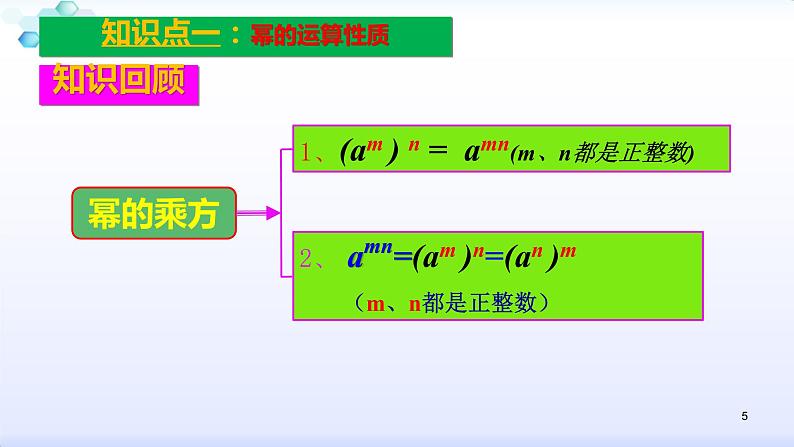
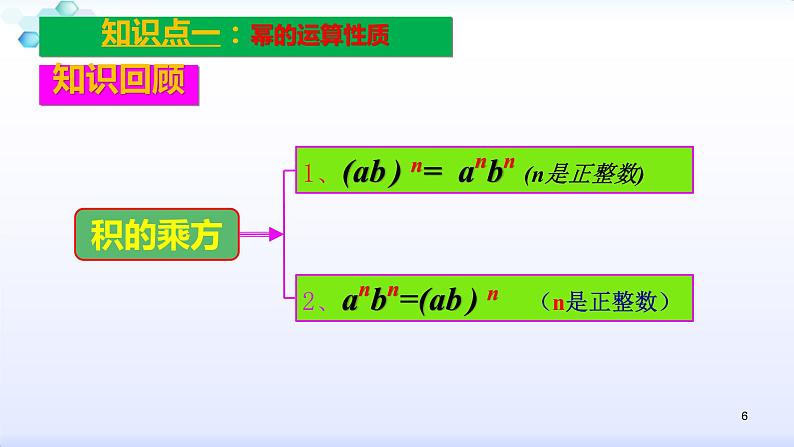
知识点一:幂的运算性质
1、am · an = am+n(m、n都是正整数)
2、am+n=am · an(m、n都是正整数)
1、(am ) n = amn(m、n都是正整数)
2、 amn=(am )n=(an )m (m、n都是正整数)
1、(ab ) n= anbn (n是正整数)
2、anbn=(ab ) n (n是正整数)
1.约定:a☒b=10a×10b,如:2☒3=102×103=105,则4☒8为( ) A.32 B.1032 C.1012 D.10102.当x2=a,x3=b时,x7等于( )A.2a+b B.a2b C .2ab D.ab23.若3m-1=81,则m2= .4.计算:(4×2n)×(- 4×2n)= .
5.若xn=2,则x3n的值是( )A. 6 B. 8 C.9 D. 126.如果(9n)2 =312,那么n的值是( )A.4 B.3 C.2 D. 17.计算2m・4n的结果是( )A.(2×4)m+n B.2×2m+n C.2n×2m D.2m+2n8.若3×9m×27m=321 ,则m= .
9.计算(﹣ )2019×( )2020,结果正确的是( )A. B.﹣ C. D.﹣10.若x2n=2,y3n=3,则(xy)6n= .11.(﹣0.125)2019×82020等于( )A. ﹣8 B. 8 D.﹣0.12512.若∣a﹣2∣+(b+0.5)2=0,则a11b11= .
1.(易错题)若(1-x)1-3x=1,则x的取值有( )个. A.0 B.1 C.2 D.32.若3x=4,9y=7,则3x-2y的值为 .3.已知am=3,an=2,则a2m-n的值为 .
4.已知:xa=4,xb=9,求(1)x a-b;(2)x 3a-2b5.已知9n·27n-1÷33n+1=81,求(n3)2÷[(n4)3÷(n3)3]的值
先独立完成导学案专题一,再同桌相互交流,最后小组交流;
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
1.x3ym-1·xm+n·y2n+2=x9y9,则 4m-3n等于( )A.8 B.9 C.10 D.无法确定2.如果xny4与2xym相乘的结果是2x5y7那么mn= .
3.已知﹣2x3m+1y2n与4xn-6y-3-m的积与﹣x4y是同类项,则m+n的值是 .4.一种计算机每秒可做4×108次运算,它工作3×104秒运算的次数为( )A.12×1012 B.1.2×1012 C.1.2×1011 D.1.2×1013
5.通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是 .6.方程2x(x﹣1)=12+x(2x﹣5)的解是 .7.先化简,再求值:x(x2+xy+y2)﹣y(x2+xy+y2)+3xy(y﹣x), 其中x= ,y=1.
8.三个连续偶数,中间一个是n,它们的积是( )A n3-n B. n3-4n C.3n3-3n D. 4n3-n9.设M=(x﹣3)(x﹣7),N=(x﹣2)(x﹣8),则M与N的关系为( )A M
(x+p)(x+q) =
x2 + (p+q) x + p q
(a+b)÷m = a÷m+b÷m(m≠0)
1.计算6m6÷(-2m2)3的结果为( ) A -m B.-1 C. D.﹣2.(1)若8a3b2÷M=2ab2,则M= . (2)若4a3bm÷9anb2= b2,则m= ,n= .3.下列计算正确的是( ) A.8x2÷23=4x3 B.4a2b3c3÷4a2b2c=bc C.﹣12x5y3z÷2x2y=﹣6x3y3z D .2ab2c÷ ab2=4c
4.下列运算中,错误的是( )A.(6a3+3a2)÷ a=12a2+6a B.(6a3-4a2+2a)÷2a=3a2-2aC.(9a7-3a3)÷(﹣ a3)=﹣27a4+9 C.( a2+a)÷(﹣ a)=﹣ a-25.一个多项式与﹣2x2的积为﹣2x5+4x3﹣x2,则这个多项式为 .6.计算:⑴ (9x2y-6xy2)÷3xy; ⑵ (3x2y-xy2+ xy)÷(- xy) .
先独立完成导学案专题二,再同桌相互交流,最后小组交流;
知识点三:乘法公式的应用
(a+b)(a-b) = a 2 - b 2
(b+a)(-b+a)=a2-b2
(-a+b)(-a-b)=(-a)2-b2
1.计算(1-m)(-m-1),结果正确的是( )A.m2-2m-1 B.m2-1 C.1-m D.m2-2m+12.三个连续整数,中间的一个是n,则这三个整数的积是( )A .3n B.n3 C.n3-1 D.n3-n 3.若x+y=6,x-y=5,则x2-y2的值是 .4.若计算(x+m)(x+ )的结果不含字母x的一次项,则 (x+m)(x-m)= .
(a+b)2= a2 +2ab+b2(a-b)2= a2 - 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(乘法的)完全平方公式:
完全平方公式是多项式乘法:(a+b)(p+q),p=a,q=﹣b的特殊情形.
4、公式中的字母a,b可以表示数,单项式和多项式.
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符号相同.
前平方,后平方,积的二倍放中央.
1.下列计算正确的是( )A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2C.(x+2y)(x-2y)=x2-2y2 D.(-x+y)2=x2-2xy+y22下列各式,计算结果是 m2n2 -mn+1的是( )A .(mn- )2 B. ( mn+1)2 C. ( mn-1)2 D. ( mn-1)23若(x-y)2=(x+y)2+( ),则括号中应填的是( )A.-2xy B. 2xy C. -4xy D. 4xy
4.( -3b)2=16a2- + .5.已知2x+y=1,则代数式(y+1)2-(y2-4x)的值为 .6.如果y2-ky+9是完全平方式,则 k= .7.利用完全平方公式计算: (1)2012 (2)1992
口诀:添括号,看符号;添“+”号,不变号;添“-”号,全变号.
添括号时,如果括号前面是“+”号,括到括号里的各项都不改变符号;如果括号前面是“-”号,括到括号里的各项都要改变符号;
1.应用平方差公式计算(x+2y﹣1)(x﹣2y+1),则下列变形正确的是( )A.[x﹣(2y+1)]2 B.[x+(2y+1)]2,C.[x+(2y﹣1)][x﹣(2y﹣1)] D.[(x﹣2y)+1][(x﹣2y)﹣1]2.下列式子中不能用乘法公式计算的是( )A.(a+b﹣c)(a﹣b+c) B.(a﹣b﹣c)2C.(2a+b+2)(a﹣2b﹣2) D.(2a+3b﹣1)(1﹣2a﹣3b).
3.计算(a+1)2(a-1)2的结果是( )A.a4-1 B.a4+1 C.a4+2a2+1 D.a4-2a2+14.利用乘法公式计算:(1) (x+2y﹣3)(x﹣2y+3) ;(2) (a+b+c)2.
杨辉三角中斜行和水平行之间的关系
把斜行①中第7行之前的数字相加得1+1+1+1+1+1+1=6 ②:1+2+3+4+5=15③:1+3+6+10=20④:1+4+10=15⑤:1+5=6⑥1
将上面得到的数字与第7行中的数字对比你有什么发现?
1.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图所示的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”根据“杨辉三角”,计算(a+b)20的展开式中第三项的系数为( )A.2017 B.2016 C.191 D.190.
先独立完成导学案专题三,再同桌相互交流,最后小组交流;
例1:已知x2-2x-1=0,求代数式(x-1)2+x(x-4)+(x-2)(x+2)的值.
解:∵ x2-2x-1=0 ∴ x2-2x=1
∴原式=x2-2x+1+x2-4x+x2-4 =3x2-6x-3 =3(x2-2x)-3=3×1-3=0
1. /x-y+1/与(x+2y+4)2互为相反数,求代数式[(2x+2y)2-(3x+y)(3x-y)-5y2]÷2x的值.2若(7x-a)2=49x2-bx+9,则/a+b/的值为( )A.18 B.24 C.39 D.453已知a-b=4,ab+c2+4=0,则a+b等于( )A.4 B.0 C.2 D.-2
4.已知(m-n)2=34,(m+n)2=4000则m2+n2的值为 .
1. 已知a=-2016,b=2017,c=-2018,求a2+b2+c2+ab+bc-ac的值.2.已知M= a-1,N=a2- a(a为任意实数),则M,N的大小关系为( )A. M<N B. M=N C. M>N D.不能确定
3.若x2+y2+ =2x+y,则y-x= .
先独立完成导学案专题四,再同桌相互交流,最后小组交流;
知识点五:因式分解及其简单应用
把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
因式分解与整式乘法是互逆过程
pa+pb+pc =p(a+b+c) 这样就把pa+pb+pc分解成两个因式乘积的形式,其中一个因式是各项的公因式p,另一个因式(a+b+c)是pa+pb+pc除以 p所得的商. 一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另ー个因式的乘积的形式,这种分解因式的方法叫做 .
1.多项式-6xyz+3xz2-9x2y中各项的公因式是( ) A.-3x B. 3xz C.3yz D. -3xy2.将- a2b-ab2提公因式后,另一个因式是( ) A. a+2b B. -a+2b C. -a-b D. a-2b3.把多项式a2-4a因式分解,正确的是( )A.a(a-4) B.(a+2)(a-2) C.a(a+2)(a-2 D.(a-2)2-44.多项式-3xy+21axy-18a2xy的公因式是 .
两个数的和与这两个数的差的积,等于这两个数的平方差.
两个数的平方差,等于这两个数的和与这两个数的差的积.
a2 - b2 = ( a + b ) ( a - b )
( a + b ) ( a - b ) = a2 - b2
(1)等号的左边是一个二项式,两项都是平方的形式且符号相反;(2)等号的右边是两个二项式的积,其中一个二项式是两个数的和,另个二项式是这两个数的差.
即:“两项、平方、异号形式”
1.分解因式:(1)9a2-4b2; (2)x2y-4y; (3) 1-(a-b)2;(4) x4-1; (5)(x+y+z)2-(x-y+z)2.
3.(易错题)两个连续奇数的平方差是( ) A.6的倍数 B.8的倍数 C.12的倍数 D.16的倍数4.已知a+b=2,则a2-b2+4b的值是( ) A.2 B.3 C.4 D.6
a2 +2ab+b2=(a+b)2 a2 - 2ab+b2=(a - b)2
即两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
1、前平方,后平方,积的二倍在中央.
2、必须是三项式(或可以看成三项的).
3、平方项符号要相同.
1.下列各式中,可以利用完全平方公式进行因式分解的是( ) A.2x2+4x+1 B.4x2-12xy+9y2 C.2x2+4xy+y2 D.x2-y2+2xy2.(易错题)若多项式x2+mx+4能用完全平方公式分解因式,则m的值是( ) A.4 B.-4 C.±8 D.±43.下列多项式中,能用完全平方公式进行因式分解的是( )A.-a2-4ab+4b2 B .a2+6ab-9b2 C.a2+2ab+4b2 D.4(a-b)2+4(a-b)+14.若a+b=4,则a2+2ab+b2的值是( ) A.16 B.8 C.4 D.2
5.若 a2b2+a2+b2+1-2ab=2ab,则a+b的值为( ) A.2或-2 B.2或-2或0 C.2 D.-26.若多项式 x2+(k-3)x+9是完全平方式,则k的值为 .
7.如图,有三种卡片,其中边长为a的正方形卡片1张,边长为a,b的长方形卡片6张,边长为b的正方形卡片9张,用这16张卡片拼成一个大正方形,则这个大正方形的边长为 .
先独立完成导学案专题五,再同桌相互交流,最后小组交流;
对自己说,你有什么收获? 对同学说,你有什么温馨提示? 对老师说,你还有什么困惑?
人教版八年级数学上册 三角形--知识点复习 优质 课件(共34张PPT): 这是一份人教版八年级数学上册 三角形--知识点复习 优质 课件(共34张PPT),共34页。PPT课件主要包含了复习目标,重点难点,知识链接,体系构建,三角形,与三角形有关的线段,三角形内角和,三角形外角和,角平分线,知识回顾等内容,欢迎下载使用。
初中数学人教版八年级上册第十四章 整式的乘法与因式分解综合与测试课堂教学ppt课件: 这是一份初中数学人教版八年级上册第十四章 整式的乘法与因式分解综合与测试课堂教学ppt课件,共14页。
初中数学人教版八年级上册第十五章 分式综合与测试复习课件ppt: 这是一份初中数学人教版八年级上册第十五章 分式综合与测试复习课件ppt,共48页。PPT课件主要包含了复习目标,重点难点,知识回顾,巩固练习,①③⑤,合作探究,分式的基本性质,用式子表示,a2-ab,约分的一般方法等内容,欢迎下载使用。













