

【江苏南通】2020-2021学年八年级数学下学期期末模拟测试卷2(含解析)
展开2020-2021学年八年级数学下学期期末模拟测试卷02(江苏南通卷)
一、选择题(本大题共10小题,每小题2分,共20分。在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.下列图形是中心对称图形的是( )
A. B. C. D.
2.已知函数y=,则自变量x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠1 C.﹣1<x<1 D.x≠1
3.如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O.添加下列条件中的一个,若可推出该四边形是平行四边形.则添加的条件可以是( )
①AD∥BC,②AB=CD,③AD=BC,④∠ADC=∠ABC,⑤BO=DO,⑥∠DBA=∠CAB.
A.①②③⑤ B.①②④⑤ C.①②④⑥ D.①③④⑥
4.已知一次函数y=kx+b的图象过二、三、四象限,则下列结论正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
5.下列说法中不正确的是( )
A.平行四边形对角线互相平分
B.矩形各内角平分线围成正方形
C.菱形对角线互相垂直平分
D.﹣组对边平行另一组对边相等的四边形是梯形
6.在AI计算机比赛预赛中,11名参赛者得分各不相同,按得分取前5名进入决赛.若佳佳知道自己的得分,要判断自己能否进入决赛,她只需知道11名参赛者得分的( )
A.方差 B.平均数 C.众数 D.中位数
7.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=( )
A. B. C.5 D.2
8.某省正加速布局以5G等为代表的战略性新兴产业.据统计,该省目前5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.按照计划,设2020年底到2022年底,全省5G基站数量的年平均率为x,根据题意列方程,得( )
A.6(1+x)2=17.34 B.17.34(1+x)2=6
C.6(1﹣x)2=17.34 D.17.34(1﹣x)2=6
9.A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④小时后两人相遇.
A.1个 B.2个 C.3个 D.4个
10.在菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则MN的最小值等于( )
A.2 B.4 C.2 D.6
二、填空题(本大题共8小题,每小题2分,共16分。不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
11.一元二次方程3x=x2的根为 .
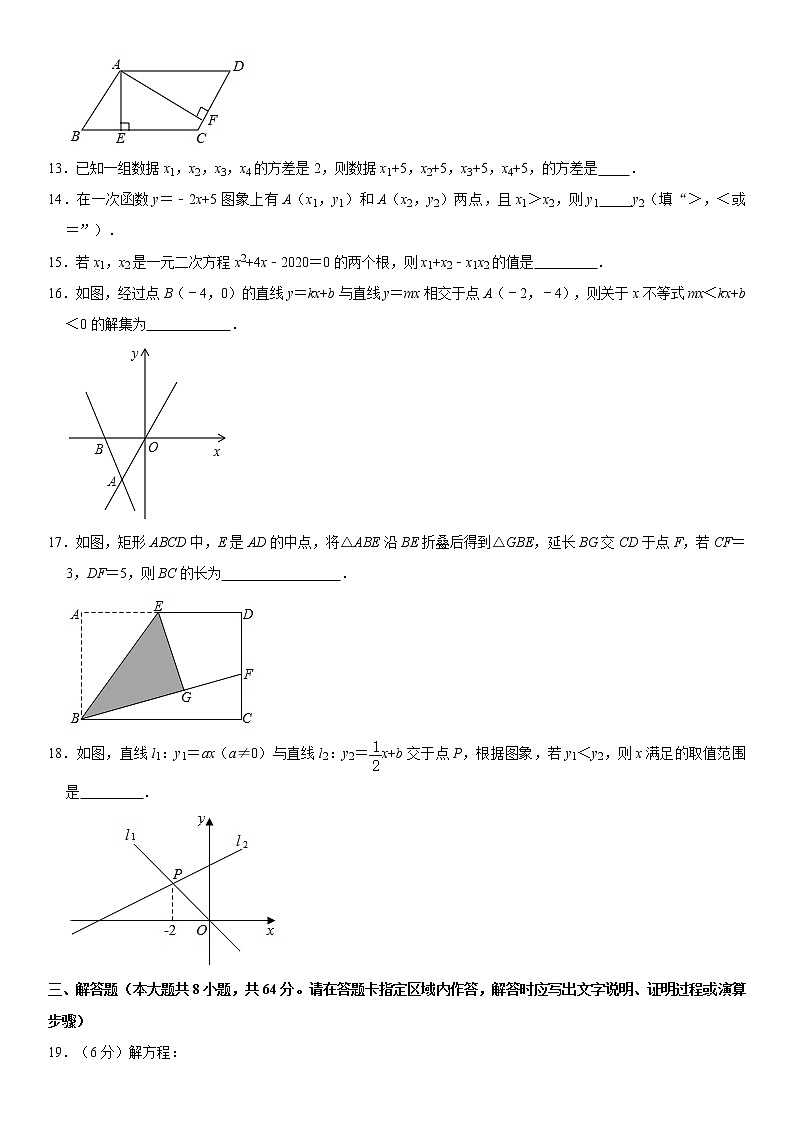
12.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=58°,则∠BAD= .
13.已知一组数据x1,x2,x3,x4的方差是2,则数据x1+5,x2+5,x3+5,x4+5,的方差是 .
14.在一次函数y=﹣2x+5图象上有A(x1,y1)和A(x2,y2)两点,且x1>x2,则y1 y2(填“>,<或=”).
15.若x1,x2是一元二次方程x2+4x﹣2020=0的两个根,则x1+x2﹣x1x2的值是 .
16.如图,经过点B(﹣4,0)的直线y=kx+b与直线y=mx相交于点A(﹣2,﹣4),则关于x不等式mx<kx+b<0的解集为 .
17.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,若CF=3,DF=5,则BC的长为 .
18.如图,直线l1:y1=ax(a≠0)与直线l2:y2=x+b交于点P,根据图象,若y1<y2,则x满足的取值范围是 .
三、解答题(本大题共8小题,共64分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(6分)解方程:
(1)3x2﹣5x﹣2=0;
(2)3x(x﹣1)=2(1﹣x).
20.(8分)2020年3月至5月,某校开展了一系列居家阅读活动.学生利用“宅家”时光,在书海中遨游,从阅读中获得精神慰藉和自我提升,为了解学生居家阅读的情况,学校从七、八两个年级各随机抽取50名学生,进行了居家阅读情况调查、下面给出了部分数据信息:
a.两个年级学生平均每周阅读时长x(单位:小时)的频数分布直方图如下(数据分成4组:0≤x<3,3≤x<6,6≤x<9,9≤x≤12):
b.七年级学生平均每周阅读时长在6≤x<9这一组的是:
6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8
c.两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如表:
平均数
中位数
众数
方差
七年级
6.3
m
8
7.0
八年级
6.0
7
7
6.3
根据以上信息,回答下列问题:
(1)补全图2;
(2)写出表中m的值;
(3)返校后,学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号,小丽说:“根据频数分布直方图中的数据信息,估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,所以七年级获得该称号的人数一定比八年级获得该称号的人数多.”你认为她的说法 (填入“正确”或“错误“);
(4)请你结合数据对两个年级的居家阅读情况进行评价.
21.(6分)如图,一次函数y=kx+b的图象经过A(2,4),B(﹣2,﹣2)两点,与y轴交于点C.
(1)求k,b的值,并写出一次函数的解析式;
(2)求点C的坐标.
22.(8分)如图,在四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,连接BD,BE,∠ABD=90°
(1)求证:四边形BCDE为菱形.
(2)连接.AC,若AC⊥BE,BC=2,求BD的长.
23.(8分)已知关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)若方程的一个根是0,求出它的另一个根及k的值.
24.(8分)如图,某校广场有一段25米长的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.
(1)求y与x的函数关系式,并指出x的取值范围;
(2)若计划修建费为150元,能否完成该草坪围栏的修建任务?若能完成,请算出利用旧围栏多少米;若不能完成,请说明理由.
25.(10分)如图,直线y=4﹣x与两坐标轴分别相交于A、B两点,过线段AB上一点M分别作MC⊥OA于点C,MD⊥OB于点D,且四边形OCMD为正方形.
(1)正方形OCMD的边长为 .
(2)将正方形OCMD沿着x轴的正方向移动,得正方形EFGH,设平移的距离为a(0<a≤4).
①当平移距离a=1时,正方形EFGH与△AOB重叠部分的面积为 ;
②当平移距离a为多少时,正方形EFGH的面积被直线AB分成1:3两个部分?
26.(10分)如图1,已知正方形ABCD的顶点A,B分别在y轴和x轴上,边CD交x轴的正半轴于点E.
(1)若A(0,a2﹣4a+5),且a=+2,求A点的坐标;
(2)在(1)的条件下,若3AO=4EO,求D点的坐标;
(3)如图2,连接AC交x轴于点F,点H是A点上方y轴上一动点,以AF、AH为边作平行四边形AFGH,使G点恰好落在AD边上,试探讨BF,HG与DG的数量关系,并证明你的结论.
2020-2021学年八年级数学下学期期末模拟测试卷02(江苏南通卷)
一、选择题(本大题共10小题,每小题2分,共20分。在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.下列图形是中心对称图形的是( )
A. B.
C. D.
解:A、不是中心对称图形,故本选项不合题意;
B、不是中心对称图形,故本选项不合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不合题意.
答案:C.
2.已知函数y=,则自变量x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠1 C.﹣1<x<1 D.x≠1
解:由函数y=有意义,得x+1≥0.
解得x≥﹣1,
答案:A.
3.如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O.添加下列条件中的一个,若可推出该四边形是平行四边形.则添加的条件可以是( )
①AD∥BC,②AB=CD,③AD=BC,④∠ADC=∠ABC,⑤BO=DO,⑥∠DBA=∠CAB.
A.①②③⑤ B.①②④⑤ C.①②④⑥ D.①③④⑥
解:①∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,故①正确;
②∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故②正确;
③∵AB∥CD,AD=BC无法得出四边形ABCD是平行四边形,故③不正确;
④∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ADC=∠ABC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,故④正确;
⑤∵AB∥CD,
∴∠ABO=∠CDO,
在△AOB和△COD中,,
∴△AOB≌△COD(ASA),
∴AO=CO,
又∵OB=OD,
∴四边形ABCD为平行四边形,故⑤正确;
∵∠BCD+∠ADC=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
⑥∵∠DBA=∠CAB,
∴OA=OB,
∵AB∥CD,
∴∠DBA=∠CDB,∠CAB=∠ACD,
∵∠DBA=∠CAB,
∴∠CDB=∠ACD,
∴OC=OD,
不能得出四边形ABCD是平行四边形,故⑥不正确;
答案:B.
4.已知一次函数y=kx+b的图象过二、三、四象限,则下列结论正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
解:∵一次函数y=kx+b的图象经过第二,三,四象限,
∴k<0,b<0,
答案:D.
5.下列说法中不正确的是( )
A.平行四边形对角线互相平分
B.矩形各内角平分线围成正方形
C.菱形对角线互相垂直平分
D.﹣组对边平行另一组对边相等的四边形是梯形
解:A、平行四边形的对角线互相平分,故本选项错误;
B、如图:
∠EBC+∠ECB=45°+45°=90°,
∴∠E=180°﹣90°=90°,
同理∠G=∠AFB=∠DHC=90°,
∴∠E=∠EFG=∠G=90°,
∴四边形EFGH是矩形,
∵∠EBC=∠ECB=45°,
∴BE=CE,
在△AFB和△DHC中
,
∴△AFB≌△DHC,
∴BF=CH,
∵BE=CE,
∴EF=EH,
∴矩形EFGH是正方形,故本选项错误;
C、菱形的对角线互相垂直平分,故本选项错误;
D、一组对边相等,另一组对边平行的四边形可能是等腰梯形,也可能是平行四边形,故本选项正确.
答案:D.
6.在AI计算机比赛预赛中,11名参赛者得分各不相同,按得分取前5名进入决赛.若佳佳知道自己的得分,要判断自己能否进入决赛,她只需知道11名参赛者得分的( )
A.方差 B.平均数 C.众数 D.中位数
解:由于总共有11个人,且他们的分数各不相同,第6名的成绩是中位数,要判断是否进入前5名,故应知道自己的成绩和中位数.
答案:D.
7.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=( )
A. B. C.5 D.2
解:由旋转变换的性质可知,△ADE≌△ABF,
∴∠ABF=∠D=90°,
∵∠ABC=90°,
∴∠ABF+∠ABC=180°,
∴C,B,F共线,
根据题意得:BC=5,BF=DE=1,
∴FC=6,CE=4,
∴EF===2.
答案:D.
8.某省正加速布局以5G等为代表的战略性新兴产业.据统计,该省目前5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.按照计划,设2020年底到2022年底,全省5G基站数量的年平均率为x,根据题意列方程,得( )
A.6(1+x)2=17.34 B.17.34(1+x)2=6
C.6(1﹣x)2=17.34 D.17.34(1﹣x)2=6
解:依题意,得:1.5×4(1+x)2=17.34,
即6(1+x)2=17.34.
答案:A.
9.A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④小时后两人相遇.
A.1个 B.2个 C.3个 D.4个
解:甲骑车速度为=30km/小时,乙的速度为=20km/小时,故①正确,
设l1的表达式为y=kx+b,把(0,80),(1,50)代入得到:,
解得,
∴直线l1的解析式为y=﹣30x+80,故②正确,
设直线l2的解析式为y=k′x,把(3,60)代入得到k′=20,
∴直线l2的解析式为y=20x,故③正确,
由,解得x=,
∴小时后两人相遇,故④正确,
答案:D.
10.在菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则MN的最小值等于( )
A.2 B.4 C.2 D.6
解:连接BD、BF,延长AC交GE于H,连接BH,如图所示:
∵四边形ABCD和四边形BEFG是菱形,∠DAB=60°,
∴AD∥BC∥GF,AC⊥BD,BF⊥GE,BE=BG,AM=CM,EN=GN,
∴∠GAH=30°,∠EBG=∠DAB=60°,
∴△BEG是等边三角形,
∴∠BGE=60°,
∴∠AHG=90°,
∴四边形BNHM是矩形,GH=AG=4,AH=GH=4,
∴MN=BH,当BH⊥AG时,BH最小,
∵∠GAH=30°,
∴BH=AH=2,
∴MN的最小值=2;
答案:A.
二、填空题(本大题共8小题,每小题2分,共16分。不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
11.一元二次方程3x=x2的根为 x1=0,x2=3 .
解:x2﹣3x=0,
x(x﹣3)=0,
x=0或x﹣3=0,
所以x1=0,x2=3.
答案:x1=0,x2=3.
12.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=58°,则∠BAD= 122° .
解:∵AE⊥BC于点E,AF⊥CD于点F,
∴∠AEC=∠AFC=90°,
又∵∠EAF=58°,
∴∠C=360°﹣58°﹣90°﹣90°=122°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠C=122°.
答案:122°.
13.已知一组数据x1,x2,x3,x4的方差是2,则数据x1+5,x2+5,x3+5,x4+5,的方差是 2 .
解:∵数据x1,x2,x3,x4的方差是2,
∴数据x1+5,x2+5,x3+5,x4+5的方差是2.
答案:2.
14.在一次函数y=﹣2x+5图象上有A(x1,y1)和A(x2,y2)两点,且x1>x2,则y1 < y2(填“>,<或=”).
解:∵一次函数y=﹣2x+5中,k=﹣2<0,
∴y随x的增大而减小.
∵x1>x2,
∴y1<y2.
答案:<.
15.若x1,x2是一元二次方程x2+4x﹣2020=0的两个根,则x1+x2﹣x1x2的值是 2016 .
解:∵x1,x2是一元二次方程x2+4x﹣2020=0的两个根,
∴x1+x2=﹣4,x1x2=﹣2020,
则x1+x2﹣x1x2=﹣4﹣(﹣2020)=2016,
答案:2016.
16.如图,经过点B(﹣4,0)的直线y=kx+b与直线y=mx相交于点A(﹣2,﹣4),则关于x不等式mx<kx+b<0的解集为 ﹣4<x<﹣2 .
解:根据图象可得关于x的不等式mx<kx+b<0的解集是﹣4<x<﹣2.
答案:﹣4<x<﹣2.
17.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,若CF=3,DF=5,则BC的长为 4 .
解:过点E作EM⊥BC于M,交BF于N,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
在△ENG与△BNM中,
,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴CM=DE,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM=CF=,
∴NG=,
∵BG=AB=CD=CF+DF=8,
∴BN=BG﹣NG=8﹣=,
∴BF=2BN=13,
∴BC===4.
答案:4.
18.如图,直线l1:y1=ax(a≠0)与直线l2:y2=x+b交于点P,根据图象,若y1<y2,则x满足的取值范围是 x>﹣2 .
解:如图,直线l1:y1=ax(a≠0)与直线l2:y2=x+b交于点P,点P的横坐标是﹣2,
所以若y1<y2,则x满足的取值范围是x>﹣2.
答案:x>﹣2.
三、解答题(本大题共8小题,共64分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.解方程:
(1)3x2﹣5x﹣2=0;
(2)3x(x﹣1)=2(1﹣x).
解:(1)方程3x2﹣5x﹣2=0,
分解因式得:(3x+1)(x﹣2)=0,
可得3x+1=0或x﹣2=0,
解得:x1=﹣,x2=2.
(2)∵3x(x﹣1)=2(1﹣x),
∴3x(x﹣1)+2(x﹣1)=0,
∴(x﹣1)(3x+2)=0,
∴x﹣1=0或3x+2=0,
∴x1=1,x2=﹣.
20.2020年3月至5月,某校开展了一系列居家阅读活动.学生利用“宅家”时光,在书海中遨游,从阅读中获得精神慰藉和自我提升,为了解学生居家阅读的情况,学校从七、八两个年级各随机抽取50名学生,进行了居家阅读情况调查、下面给出了部分数据信息
a.两个年级学生平均每周阅读时长x(单位:小时)的频数分布直方图如下(数据分成4组:0≤x<3,3≤x<6,6≤x<9,9≤x≤12):
b.七年级学生平均每周阅读时长在6≤x<9这一组的是:
6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8
c.两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如表:
平均数
中位数
众数
方差
七年级
6.3
m
8
7.0
八年级
6.0
7
7
6.3
根据以上信息,回答下列问题:
(1)补全图2;
(2)写出表中m的值;
(3)返校后,学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号,小丽说:“根据频数分布直方图中的数据信息,估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,所以七年级获得该称号的人数一定比八年级获得该称号的人数多.”你认为她的说法 错误 (填入“正确”或“错误“);
(4)请你结合数据对两个年级的居家阅读情况进行评价.
解:(1)八年级学生每周阅读时间在6≤x<9人数为:50﹣6﹣13﹣9=22(人),
补全的统计图如图所示:
(2)将七年级学生每周阅读时间从小到大排列后处在第25、26位的两个数的平均数为=6.5,
即,m=6.5;
(3)根据频数分布直方图中的数据估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,
由于不知道各个年级的人数,虽然七年级学生获得称号的比例大,也不能说七年级获得该称号的人数一定比八年级的多,
因此这种说法不正确,
答案:错误;
(4)从平均数上看,七年级学生每周阅读时间要高于八年级,而七年级的方差较大,说明七年级学生阅读时间的离散程度较大,不稳定,
从中位数上看,八年级的高于七年级,说明八年级学生每周阅读时间小于7小时,大约占一半,八年级的方差较小,八年级学生的阅读时间比较稳定,比较集中在某个数的附近,波动不大.
21.如图,一次函数y=kx+b的图象经过A(2,4),B(﹣2,﹣2)两点,与y轴交于点C.
(1)求k,b的值,并写出一次函数的解析式;
(2)求点C的坐标.
解:(1)把A(2,4),B(﹣2,﹣2)代入y=kx+b得:,解得,
∴一次函数的解析式为:y=x+1;
(2)把x=0代入y=x+1中得:y=1,
∴C(0,1).
22.如图,在四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,连接BD,BE,∠ABD=90°
(1)求证:四边形BCDE为菱形.
(2)连接.AC,若AC⊥BE,BC=2,求BD的长.
(1)证明:∵∠ABD=90°,E是AD的中点,
∴BE=DE=AE,
∵AD=2BC,
∴BC=DE,
∵AD∥BC,
∴四边形BCDE为平行四边形,
∵BE=DE,
∴四边形BCDE为菱形;
(2)解:由(1)得:四边形BCDE为菱形,
∴BC=BE,
∵AD∥BC,
∴四边形ABCE为平行四边形,
∵AC⊥BE,
∴四边形ABCE为菱形,
∴BC=AB=2,AD=2BC=4,
∵∠ABD=90°,
∴BD===.
23.已知关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)若方程的一个根是0,求出它的另一个根及k的值.
解:(1)∵关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有两个不相等的实数根,
∴b2﹣4ac=[2(k﹣1)]2﹣4(k2﹣1)>0,
解得:k<1;
(2)∵方程的一个根是0,
∴代入方程得:k2﹣1=0,
解得:k=±1,
∵k<1,
∴k=﹣1,
∴原方程为:x2+2(﹣1﹣1)x=0,
解得:x1=0,x2=4,
则k=﹣1时,另一根是x=4.
24.如图,某校广场有一段25米长的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.
(1)求y与x的函数关系式,并指出x的取值范围;
(2)若计划修建费为150元,能否完成该草坪围栏的修建任务?若能完成,请算出利用旧围栏多少米;若不能完成,请说明理由.
解:(1)y=1.75x+4.5(×2+x),
=1.75x++4.5x,
=6.25x+(0<x≤25);
(2)当y=150时,6.25x+=150
整理得:x2﹣24x+144=0
解得:x1=x2=12
经检验,x=12是原方程的解,且符合题意.
答:应利用旧围栏12米.
25.如图,直线y=4﹣x与两坐标轴分别相交于A、B两点,过线段AB上一点M分别作MC⊥OA于点C,MD⊥OB于点D,且四边形OCMD为正方形.
(1)正方形OCMD的边长为 2 .
(2)将正方形OCMD沿着x轴的正方向移动,得正方形EFGH,设平移的距离为a(0<a≤4).
①当平移距离a=1时,正方形EFGH与△AOB重叠部分的面积为 ;
②当平移距离a为多少时,正方形EFGH的面积被直线AB分成1:3两个部分?
解:(1)设点M(x,4﹣x),
∵当四边形OCMD为正方形时,OC=CM,即x=4﹣x,
∴x=2,
∴CM=OC=2,
答案:2;
(2)①∵直线AB的解析式为y=﹣x+4,
∴移动过程中正方形EFGH被分割出的三角形是等腰直角三角形,
如图1,
∵四边形EFGH是正方形,
∴正方形EFGH的面积=22=4,
当a=1时,EM=1,
∴S△MQE=EM2=,
∴正方形EFGH与△AOB重叠部分的面积=4﹣=;
答案:;
②∵正方形EFGH的面积被直线AB分成1:3两个部分,
∴两部分的面积分别为1和3.
当0<a≤2时,如图2所示:
∵直线AB的解析式为y=4﹣x,
∴∠BAO=45°,
∴△MQE为等腰直角三角形,
∴EQ=ME,
∴ME2=1,
∴ME=,即a=,
当2<a<4时,如图3所示:
∵∠BAO=45°,
∴△AGQ为等腰直角三角形.
∴GQ=GA.
∴GA2=1,解得:GA=.
∵将y=0代入y=4﹣x得:4﹣x=0,
∴x=4,
∴OA=4.
∴OG=4﹣,即a=4﹣.
综上所述,当平移的距离为a=或a=4﹣时,正方形EFGH的面积被直线AB分成1:3两个部分.
26.如图1,已知正方形ABCD的顶点A,B分别在y轴和x轴上,边CD交x轴的正半轴于点E.
(1)若A(0,a2﹣4a+5),且a=+2,求A点的坐标;
(2)在(1)的条件下,若3AO=4EO,求D点的坐标;
(3)如图2,连接AC交x轴于点F,点H是A点上方y轴上一动点,以AF、AH为边作平行四边形AFGH,使G点恰好落在AD边上,试探讨BF,HG与DG的数量关系,并证明你的结论.
(1)解:∵a=+2,
∴(a﹣2)2=3,
∴a2﹣4a+4=3,
∴a2+4a+5=4,
即A点的坐标为(0,4);
(2)解:作DN⊥OE于N,作AM⊥DN于M,连AE,如图1所示:
则∠BAD=∠OAM=90°,
即∠BAO+∠OAD=∠OAD+∠DAM,
∴∠BAO=∠DAM,
∵四边形ABCD是正方形,
∴AB=AD,∠ADE=90°,
在△AOB与△AMD中,,
∴△AOB≌△AMD(AAS),
∴AM=AO=4,
∴四边形AONM是正方形,
∴MN=ON=4,
∵3AO=4EO,
∴EO=3,
在Rt△AOE中,AE2=AO2+EO2=42+32=25,
在Rt△AMD中,AD2=AM2+DM2,
在Rt△DNE中,ED2=EN2+DN2,
在Rt△ADE中,AD2+DE2=AE2,
∴AM2+DM2+EN2+DN2=25,
设D(4,m),则DM=4﹣m,EN=4﹣3=1,DN=m,
∴42+(4﹣m)2+12+m2=25,
∴m=2,
∴D(4,2)
(3)解:2HG2+DG2=4BF2,理由如下:
过点F作FP⊥AD于P,连DF,如图2所示:
∵四边形AFGH是平行四边形,
∴HG=AF,AH∥GF,
∴∠FGA=∠GAH,
∴∠FGD=∠OAG,
∵四边形ABCD是正方形,
∴BC=DC,∠CAD=∠BCF=∠DCF=45°,∠BAD=∠CDA=∠ABC=90°,
∴△APF是等腰直角三角形,
∴HG=AF=PF,
∴PF=,
在△BCF和△DCF中,,
∴△BCF≌△DCF(SAS),
∴BF=DF,∠CBF=∠CDF,
∵∠FDG=90°﹣∠CDF,∠ABO=90°﹣∠CBF,
∴∠FDG=∠ABO,
∵∠OAG+∠OAB=90°,∠ABO+∠OAB=90°,
∴∠OAG=∠ABO,
∴∠FGD=∠FDG,
∴GF=DF=BF,
∴点P是DG的中点,
∴DP=,
在Rt△PDF中,PF2+DP2=DF2,
即()2+()2=BF2,
∴2HG2+DG2=4BF2.
【江苏徐州卷】2020-2021学年八年级数学下学期期末模拟测试卷2(含解析): 这是一份【江苏徐州卷】2020-2021学年八年级数学下学期期末模拟测试卷2(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【江苏南通卷】模拟卷04-2020-2021学年八年级数学下学期期末模拟测试卷4(含解析): 这是一份【江苏南通卷】模拟卷04-2020-2021学年八年级数学下学期期末模拟测试卷4(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【江苏南通卷】2020-2021学年八年级数学下学期期末模拟测试卷5(含解析): 这是一份【江苏南通卷】2020-2021学年八年级数学下学期期末模拟测试卷5(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












