数学八年级上册4 分式方程教学演示课件ppt

这是一份数学八年级上册4 分式方程教学演示课件ppt，共54页。PPT课件主要包含了Contents，观察发现，随堂练习，课堂小结，问题情境，做一做，只要人人都献出一点爱，知识深化，大显身手，知识回顾等内容，欢迎下载使用。

甲、乙两地相距1400km，从甲地到乙地乘高铁列车比乘特快列车少用9h，已知高铁列车的平均行驶速度是特快列车的2.8倍。
你能找出这一问题中的所有等量关系吗？
乘特快列车所需时间-乘高铁所需时间=9h
高铁速度=特快列车速度的2倍
为了帮助遭受自然灾害地区重建家园，某学校号召同学自愿捐款。已知七年级同学捐款总额为4800元，八年级同学捐款总额为5000元，八年级捐款人数比七年级多20人，而且两个年级人均捐款额恰好相等。如果设七年级捐款人数为x人，那么x满足怎样的方程？
观察上面的几个方程，有什么共同特点？
共同点：这几个方程分母中都含有未知数
分母中含有未知数的方程叫做分式方程
1.找找看，下列方程哪些是分式方程：
2.“退耕还林还草”是在我国西部地区实施一项重要生态工程。某地规划退耕面积共69000 ，退耕还林与退耕还草的面积比为5∶3，设退耕还林的面积为x ，那么x满足怎样的分式方程？
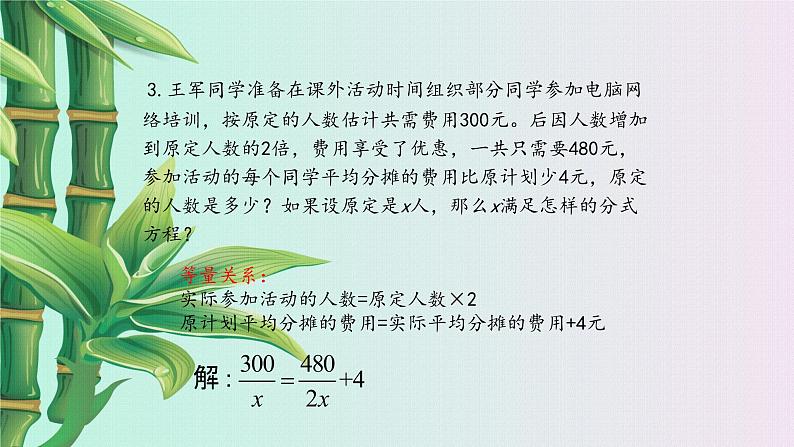
3.王军同学准备在课外活动时间组织部分同学参加电脑网络培训，按原定的人数估计共需费用300元。后因人数增加到原定人数的2倍，费用享受了优惠，一共只需要480元，参加活动的每个同学平均分摊的费用比原计划少4元，原定的人数是多少？如果设原定是x人，那么x满足怎样的分式方程？
等量关系：实际参加活动的人数=原定人数×2原计划平均分摊的费用=实际平均分摊的费用+4元
什么是分式方程？分式方程与整式方程的联系与区别。分式方程是刻画现实生活的又一数学模型； 要注意掌握列方程的最基本的思维步骤。
还记得什么是方程的解吗？你能设法求出上一节课列出的分式 方程 的解吗？
你能否从中总结出分式方程 的解法？
你还有不同于例题的解法吗？
解分式方程一般需要哪几个步骤？去分母，化为整式方程：（1）把各分母分解因式；（2）找出各分母的最简公分母；（3）方程两边各项乘以最简公分母；解整式方程。检验。结论：确定分式方程的解。
你认为x=2是原方程的根吗？与同伴交流。
在上面的方程中，x=2不是原方程的根，因为它使得原分式方程的分母为零，我们称它为原方程的增根。 产生增根的原因，是我们在方程的两边同乘了一个可能使分母为零的整式。 因此解分式方程可能产生增根，所以解分式方程必须检验。
(1)把未知数的值代入原方程(一般方法)；(2)把未知数的值代入最简公分母(简便方法)。
这里的检验要以计算正确为前提
切记：解分式方程一定要验根噢！
试说明这样检验的理由。
说一说分式方程的解法步骤有哪几步？
方程两边都乘以 得 解这个方程，得
解分式方程容易犯的错误主要有：
1.去分母时，原方程的整式部分漏乘。2.约去分母后，分子是多项式时， 要注意添括号。 3.增根不舍掉。4.符号问题。5.……
1.解分式方程的一般步骤。2.增根与验根。3.解分式方程容易发生的错误。4.要注意灵活运用解分式方程的步骤。5.同时要有简算意识，提高运算的速度和准确性。
总结经验，掌握法宝，百战百胜
什么叫分式方程？ 什么叫增根？ 产生增根的原因是什么？列方程解应用题的一般步骤分哪几步？
审题 找等量关系 设未知数 列方程 解方程 检验 答题
分母中含有未知数的方程叫分式方程
使原分式方程的分母为零的根是原分式方程的增根
去分母时，在分式方程的两边同时乘了一个可能使分式方程的分母为零的整式。
某单位将沿街的一部分房屋出租。每间房屋的租金相同。已知每间房屋的租金第二年比第一年多500元，所有房屋出租的租金第一年为9.6万元，第二年为10.2万元。
1.你能找出这一情境中的等量关系吗？
2.根据这一情境你能提出哪些问题？
3.你能利用方程求出这两年每间房屋的租金各是多少吗？
①第一年每间房屋的租金=第二年每间房屋的租金－500元②第一年出租房屋间数=第二年出租的房屋间数
问题1.求出租的房屋总间数；问题2.分别求这两年每间房屋的租金。
问题1.求出租的房屋总间数
解：设出租的房屋总间数为x间，依题意，得
解得 x=12经检验x=12是所列方程的根所以出租的房屋总间数为12间
第一年每间房屋的租金=第二年每间房屋的租金-500元
问题2.分别求这两年每间房屋的租金
解：设第一年每间房屋的租金为x元，则第二年每间房屋的租金为（x+500）元，依题意，得
解得 x=8000经检验x=8000是所列方程的根。 x+500=8500所以，第一年每间房屋的租金为8000元，第二年每间房屋的租金为8500元。
某市从今年1月1日起调整居民用水价格，每立方米水费上涨1/3。小丽家去年12月的水费是14.7元，而今年7月份的水费是28元。已知小丽家今年7月份的用水量比去年12月份的用水量多3立方米，求该市今年居民用水的价格。
解：设该市去年用水的价格为x元/m3
( )x元/m3
今年7月份用水量-去年12月份用水量=3立方米
解得x=2.1经检验x=2.1是所列方程的根答：该市今年居民用水的价格为2.8元/m3
2.1×(1+ )=2.8(元)
小明和同学一起去书店买书，他们先用15元买了一种科普书，又用15元买了一种文学书。科普书的价格比文学书高出一半，因此他们所买的科普书比所买的文学书少1本。这种科普书和这种文学书的价格各是多少？
等量关系： 1.科普书价格=文学书价格×1.5 2.所买文学书本数-所买的科普书本数=1 3.书本数=总金额/价格
解：设文学书的价格是每本x元，则科普书每本1.5x元。依题意得：
答：文学书的价格是每本5元，科普书每本7.5元。
经检验x=5是所列方程的根。
∴1.5x=1.5×5=7.5
甲、乙两人练习骑自行车，已知甲每小时比乙多走6千米，甲骑90千米所用的时间和乙骑60千米所用时间相等，求甲、乙每小时各骑多少千米？
解：设甲每小时骑x千米，则乙每小时骑（x-6）千米。
经检验x=18是所列方程的根。
答：甲每小时骑18千米，乙每小时骑12千米。
1.利用分式方程模型解决实际问题：
---建立分式方程模型
2. 列分式方程解应用题的一般步骤（1）审：分析题意，找出研究对象，建立等量关系。（2）设：选择恰当的未知数，注意单位。（3）列：根据等量关系正确列出方程。（4）解：认真仔细。（5）验：有三种方法检验。（6）答：不要忘记写答。
2. 经历实际问题的解决过程，提高分 析问题、解决问题的能力。
能找出行程和工程问题中的等量关系学会列分式方程解应用题的方法和步骤。
1.在行程问题中，主要涉及速度、时间、路程，其中，时间=（ ）。 特别地，在水流行程中，若已知静水速度和水流速度，则顺水速度=（ ），逆水速度=（ ）。
2.在工程问题中，主要涉及工作效率、工作时间、工作总量，其中工作总量=（ ）。若小王完成一项工作，需要60天，则每天的工作效率是（ ）
3.说一说列方程解应用题的方法与步骤
审（审题，找出数量和相等的关系）
设（一般求什么设什么——这是直接设，也可间接设）
列（根据等量关系列出方程）
答（完整地写出答案，注意单位）
一艘轮船顺水航行40千米所用的时间与逆水航行30千米所用的时间相同。若水流速度是3千米/小时，求轮船在静水中的速度。
解：设轮船在静水中的速度是x千米/小时，则顺水的速度是（x+3）千米/小时，逆水的速度是（x-3）千米/小时。
经检验，x=21是所列方程的根。
答：轮船在静水中的速度是21千米/小时。
例5 甲乙两人要走3千米的路，甲的速度是乙的速度的1.2倍，甲比乙少用0.1小时。 问：甲乙两人的速度各多少？
等量关系：甲的速度=乙的速度×1.2 乙走3千米用时-甲走3千米用时=0.1
有两个等量关系时，一个设未知数一个列方程
解：设乙的速度为x千米/小时，则甲的速度为1.2x千米/小时。
解得：x=5经检验，x=5是所列方程的根。1.2x=1.2×5=6（千米/时）答：甲的速度为6千米/时，乙的速度5千米/小时。
1.甲乙两个火车站相距720千米，火车提速后，行驶速度是原来的1.2倍，从甲站到乙站的时间缩短了1.2小时，求火车原来的速度。（只设出未知数，列出方程）
解：设原来的速度是x千米/小时，则提速后的速度是1.2x千米/小时。
2.小李做90个零件与小王做120个零件所用的时间相同，他俩每小时一共做35个零件。小李小王每小时各做多少个零件？
1.这是一个 问题，等量关系有哪些？
2.如何设未知数？理由是什么？
3.列出方程，说明理由。
解：设小李每小时做x个零件，则小王每小时做（35-x）个零件。
经检验，x=15是所列方程的根。
答：小李每小时做15个零件，小王每小时做20个零件。
35-x=35-15=20（个）
某工程若由甲队去做，恰好15天完成；若由乙队去做，恰好10天完成。现由甲乙两队合作完成，需要多少天完成？（设出未知数，列出方程）
说一说列分式方程解应用题的方法与步骤
1.审（审题，找出相等的关系）
2.设（一般求什么设什么——这是直接设，也可间接设）
3.列（根据等量关系列出方程）
5.验（检验是否是分式方程的解以及是否符合实际情况）
6.答（完整地写出答案，注意单位）
1.列方程解应用题的方法与步骤
审--设--列--解--验--答
2.两类应用题：行程问题和工程问题
（1、2题只设出未知数，列出方程）
1.甲车行驶270千米与乙车行驶240千米的时间相同，甲车的速度比乙车的速度快10千米/小时。求两车的速度。
解：设乙车的速度是x千米/小时，则甲车的速度是（x+10）千米/小时。
2.甲乙两个植树队参加植树造林活动，已知甲队每小时比乙队少种3棵树，甲队种60棵树与乙队种66棵树所用的时间相等。甲乙两队每小时各种多少棵树？
解：设乙队每小时种x棵树，则甲队每小时种（x-3）棵树。