2018-2019学年广州市番禺区八上期末数学试卷

这是一份2018-2019学年广州市番禺区八上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 如图，△ABO 关于 x 轴对称，点 A 的坐标为 1,−2，则点 B 的坐标为
A. 2,1B. 1,2C. −1,2D. −1,−2

2. 下列运算正确的是
A. a2⋅a3=a6B. a23=a6C. a6÷a2=a3D. 23=6

3. 下列长度的三条线段能组成三角形的是
A. 2，3，5B. 3，6，11C. 6，8，10D. 3，2，1

4. 小时候我们用肥皂水吹泡泡，其泡沫的厚度约 0.000326 毫米，用科学记数法表示为
A. 3.26×10−4 毫米B. 0.326×10−4 毫米
C. 3.26×10−4 厘米D. 32.6×10−4 厘米

5. 如图，将边长为 3a 的正方形沿虚线剪成两块正方形和两块长方形，若拿掉边长为 2b 的小正方形后，再将剩下的三块拼成一个矩形，则这个矩形的面积为
A. 9a2−4b2B. 3a+2bC. 6a2+2b2D. 9a2−6ab

6. 要使分式 x2−1x−1 有意义，则 x 的取值范围是
A. x≠1B. x≠−1C. x≠±1D. 任何数都可以

7. 若 x2+2m−3x+16 是完全平方式，则 m 的值等于
A. 3B. −5C. 7D. 7 或 −1

8. 一个 n 边形的内角和为 540∘，则 n 的值为
A. 4B. 5C. 6D. 7

9. 如图，在 △ABC 中，点 D 在 BC 边上，BD=AD=AC，E 为 CD 的中点，若 ∠CAE=16∘，则 ∠B 的大小为
A. 32∘B. 36∘C. 37∘D. 74∘

10. 已知 1x−1y=3，则代数式 2x+3xy−2yx−xy−y 的值是
A. −72B. −112C. 92D. 34

二、填空题（共6小题；共30分）
11. 计算：x+1x+2= ．

12. 分式方程 32x−1=1 的解是 ．

13. 因式分解：x2−9= ．

14. 一个等腰三角形的一个角为 50∘，则它的顶角的度数是 ．

15. 等腰三角形的底角是 15∘，腰长为 10，则其腰上的高为 ．

16. 如图，点 D，E 在 △ABC 边上，沿 DE 将 △ADE 翻折，点 A 的对应点为点 Aʹ，∠AʹEC=α，∠AʹDB=β，且 α<β，则 ∠A 等于 （用含 α，β 的式子表示）．

三、解答题（共9小题；共117分）
17. 分解因式：
（1）ax+ay．
（2）x4−b4．
（3）3ax2−6axy+3ay2．

18. 如图，已知 △ABC，AC（1）尺规作图：作 △ABC 的边 BC 上的高 AD（不写作法，保留作图痕迹）．
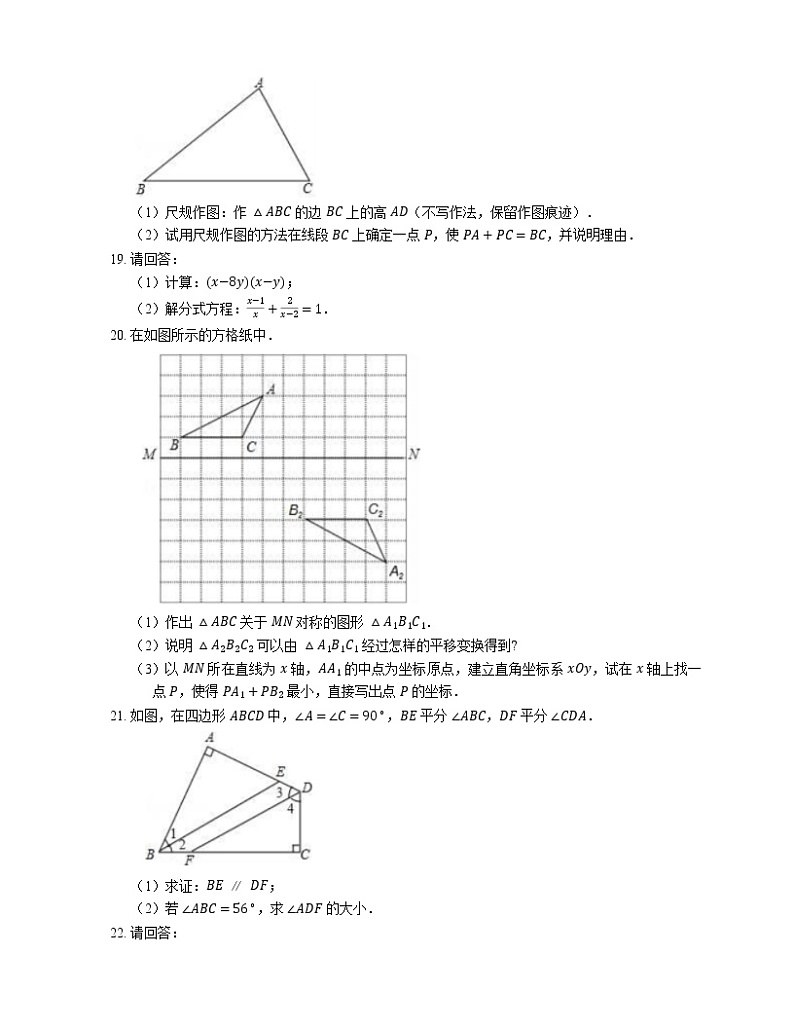
（2）试用尺规作图的方法在线段 BC 上确定一点 P，使 PA+PC=BC，并说明理由．

19. 请回答：
（1）计算：x−8yx−y；
（2）解分式方程：x−1x+2x−2=1．

20. 在如图所示的方格纸中．
（1）作出 △ABC 关于 MN 对称的图形 △A1B1C1．
（2）说明 △A2B2C2 可以由 △A1B1C1 经过怎样的平移变换得到?
（3）以 MN 所在直线为 x 轴，AA1 的中点为坐标原点，建立直角坐标系 xOy，试在 x 轴上找一点 P，使得 PA1+PB2 最小，直接写出点 P 的坐标．

21. 如图，在四边形 ABCD 中，∠A=∠C=90∘，BE 平分 ∠ABC，DF 平分 ∠CDA．
（1）求证：BE∥DF；
（2）若 ∠ABC=56∘，求 ∠ADF 的大小．

22. 请回答：
（1）计算：ab32c2÷−5a2b24c2d；
（2）先化简，再求值：x+2+52−x⋅2x−43−x，其中 x=−32．

23. 如图，在 △ABC 中，∠ACB=90∘，AC=BC，D 是 AB 边上一点（点 D 与 A，B 不重合），连接 CD，过点 C 作 CE⊥CD，且 CE=CD，连接 DE 交 BC 于点 F，连接 BE．
（1）求证：AB⊥BE；
（2）当 AD=BF 时，求 ∠BEF 的度数．

24. 某校为创建“书香校园”，购置了一批图书，已知购买科普类图书花费 10000 元，购买文学类图书花费 9000 元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵 5 元，且购买科普类图书的数量与购买文学类图书的数量相等．求科普类图书平均每本的价格．

25. 阅读下面的学习材料（研学问题），尝试解决问题：
（1）某学习小组在学习时遇到如下问题：如图①，在 Rt△ABC 中，∠C＝90∘，D 为边 BC 上一点，DA=DB，E 为 AD 延长线上一点，∠AEB=120∘，猜想 BC，EA，EB 的数量关系，并证明结论．
大家经探究发现：过点 B 作 BF⊥AE 交 AE 的延长线于 F，如图②所示，构造全等三角形使问题容易求解，请写出解答过程．
参考上述思考问题的方法，解答下列问题：
（2）如图③，等腰 △ABC 中，AB=AC，H 为 AC 上一点，在 BC 的延长线上顺次取点 E，F，在 CB 的延长线上取点 BD，使 EF=DB，过点 E 作 EG∥AC 交 DH 的延长线于点 G，连接 AF，若 ∠HDF+∠F=∠BAC．
（1）探究 ∠BAF 与 ∠CHG 的数量关系；
（2）请在图中找出一条和线段 AF 相等的线段，并证明你的结论．
答案
第一部分
1. B【解析】由题意，可知点 B 与点 A 关于 x 轴对称，
又 ∵ 点 A 的坐标为 1,−2，
∴ 点 B 的坐标为 1,2．
2. B【解析】A、 a2⋅a3=a5，原式错误，故本选项错误；
B、 a23=a6，计算正确，故本选项正确；
C、 a6÷a2=a4，原式错误，故本选项错误；
D、 23=8，原式错误，故本选项错误．
故选：B．
3. C【解析】根据三角形任意两边的和大于第三边，得A中，2+3=5，不能组成三角形；
B中，3+6=9<11，不能组成三角形；
C中，6+8=14>10，能够组成三角形；
D中，1+2=3，不能组成三角形．
4. A
5. A
【解析】∵ 阴影部分面积 =9a2−4b2，
∴ 将阴影部分的三块拼成一个矩形，则这个矩形的面积为 9a2−4b2．
6. A【解析】要使分式有意义，则 x−1≠0，解得 x≠1．
7. D【解析】∵x2+2m−3x+16 是完全平方式，
∴m−3=±4，
解得：m=7或−1．
8. B【解析】根据题意，得 n−2⋅180∘=540∘，
解得：n=5．
9. C【解析】∵AD=AC，点 E 是 CD 中点，
∴AE⊥CD，
∴∠AEC=90∘，
∴∠C=90∘−∠CAE=74∘，
∵AD=AC，
∴∠ADC=∠C=74∘，
∵AD=BD，
∴2∠B=∠ADC=74∘，
∴∠B=37∘．
10. D
【解析】∵ 1x−1y=3，
∴ y−xxy=3，
∴ x−y=−3xy，则
原式=2x−y+3xyx−y−xy=−6xy+3xy−3xy−xy=−3xy−4xy=34.
第二部分
11. x2+3x+2
【解析】原式=x2+2x+x+2=x2+3x+2.
12. x=2
【解析】去分母得：2x−1=3，
解得：x=2，
经检验 x=2 是分式方程的解．
13. x+3x−3
【解析】原式=x+3x−3．
14. 50∘ 或 80∘
【解析】（1）当 50∘ 角为顶角，顶角度数即为 50∘；
（2）当 50∘ 为底角时，顶角 =180∘−2×50∘=80∘．
15. 5
【解析】如图，
△ABC 中，∠B=∠ACB=15∘，
∴∠BAC=180∘−15∘×2=150∘，
∴∠CAD=180∘−150∘=30∘，
∵CD 是腰 AB 边上的高，
∴CD=12AC=12×10=5 cm．
16. 12β−12α
【解析】由折叠的性质可知，∠ADE=∠AʹDE=12180∘−β=90∘−12β，
∠AED=∠AʹED，
设 ∠DEC=x，
则 180∘−x=α+x，
解得，x=90∘−12α，
∴∠A=∠DEC−∠ADE=12β−12α，
故答案为：12β−12α．
第三部分
17. （1） ax+ay=ax+y.
（2） x4−b4=x2+b2x2−b2=x2+b2x+bx−b.
（3） 3ax2−6axy+3ay2=3ax2−2xy+y2=3ax−y2.
18. （1） 如图所示：AD 即为所求．
（2） 如图所示：点 P 即为所求．
理由：
∵MN 垂直平分线段 AB，
∴AP=BP，
∴PA+PC=BP+PC=BC．
19. （1） 原式=x2−9xy+8y2.
（2） 去分母得：
x2−3x+2+2x=x2−2x.
解得：
x=−2.
经检验 x=−2 是分式方程的解．
20. （1） 如图所示，△A1B1C1 即为所求．
（2） △A2B2C2 可以由 △A1B1C1 向右平移 6 个单位，向下平移 2 个单位得到．
（3） 如图，连接 AB2，交 x 轴于 P，连接 A1P，则 PA1+PB2 最小，此时，点 P 的坐标为 1,0．
21. （1） ∵∠A=∠C=90∘，
∴∠ABC+∠ADC=180∘，
∵BE 平分 ∠ABC，DF 平分 ∠ADC，
∴∠1=∠2=12∠ABC，∠3=∠4=12∠ADC，
∴∠1+∠3=12∠ABC+∠ADC=12×180∘=90∘，
又 ∠1+∠AEB=90∘，
∴∠3=∠AEB，
∴BE∥DF．
（2） ∵∠ABC=56∘，
∴∠ADC=360∘−∠A−∠C−∠ABC=124∘，
∵DF 平分 ∠CDA，
∴∠ADF=12∠ADC=62∘．
22. （1） 原式=ab32c2⋅4c2d−5a2b2=−2bd5a.
（2） 原式=2+x2−x+52−x⋅2x−23−x=3+x3−x−x−2⋅2x−23−x=−23+x=−2x−6.
当 x=−32 时，
原式=3−6=−3.
23. （1） ∵∠ACB=90∘，AC=BC，
∴∠A=∠ABC=45∘，
∵CE⊥CD，
∴∠DCE=90∘，
∴∠ACB=∠DCE，
∴∠ACD=∠BCE，且 AC=BC，CD=CE，
∴△ACD≌△BCESAS，
∴∠A=∠CBE=45∘，
∵∠ABE=∠ABC+∠CBE=45∘+45∘=90∘，
∴AB⊥BE．
（2） ∵△ACD≌△BCE，
∴AD=BE，
∵AD=BF，
∴BE=BF，且 ∠CBE=45∘，
∴∠BEF=∠BFE=67.5∘．
24. 设科普类图书平均每本的价格为 x 元，则文学类图书平均每本的价格为 x−5 元，
根据题意得：
10000x=9000x−5.
解得：
x=50.
经检验，x=50 是所列分式方程的解，且符合题意．
答：科普类图书平均每本的价格为 50 元．
25. （1） 如图②中，结论：BC=AE+12BE．理由如下，
∵ DA=DB，
∴ ∠DBA=∠DAB，
∵ AF⊥BF，
∴ ∠F=∠C=90∘，
在 △BAF 和 △ABC 中，∠F=∠C=90∘,∠BAF=∠ABC,AB=BA,
∴ △BAF≌△ABCAAS，
∴ BC=AF，
∵ ∠AEB=120∘=∠F+∠FBE，
∴ ∠FBE=30∘，
∴ EF=12BE，
∴ BC=AF=AE+EF=AE+12BE，
∴ BC=AE+12BE．
（2） （1）如图③中，
∵ ∠HDF+∠F=∠BAC，
∴∠CHG=∠FDG+∠DCH=∠FDG+∠F+∠CAF=∠BAC+∠CAF=∠BAF,
∴ ∠CHG=∠BAF；
（2）结论：AF=DG．理由如下，
如图③中，延长 BD 到 R，使得 BR=CF，连接 AR，作 AJ∥CF 交 EG 的延长线于 J，连接 FJ．
∵ AJ∥CE，AC∥JE，
∴ 四边形 ACEJ 是平行四边形，
∴ AJ=CE，AC=JE，
∵ AB=CA，
∴ JE=AB，
∵ AB=AC，
∴ ∠ABC=∠ACB，
∴ ∠ABR＝∠ACF，
在 △ABR 和 △ACF 中，AB=AC,∠ABR=∠ACF,BR=CF,
∴ △ABR≌△ACFSAS，
∴ AR=AF，
∵ BR=CF，BD=EF，
∴ DR=CE=AJ，EF=BF，
∵ AJ∥RD，
∴ 四边形 ARDJ 是平行四边形，
∴ JD=AR=AF，
在 △ABF 和 △JED 中，AB=JE,AF=JD,BF=ED,
∴ △ABF≌△JEDSSS，
∴ ∠1=∠BAF，
∵ ∠BAF=∠CHG=∠2，
∴ ∠1=∠2，
∴ DG=FJ，
∴ AF=DG．