

2018-2019学年广东省广州市番禺区九上期末数学试卷
展开一、选择题(共10小题;共50分)
1. 一元二次方程是 x2+x=0 的根的是
A. x1=0,x2=1B. x1=1,x2=−1C. x1=0,x2=−1D. x1=x2=−1
2. 下列图形中,既是轴对称图形又是中心对称图形的是
A. B.
C. D.
3. 在 ⊙O 中,弦 AB 的长为 23 cm,圆心 O 到 AB 的距离为 1 cm,则 ⊙O 的半径是
A. 2B. 3C. 3D. 2
4. 已知关于 x 的一元二次方程 ax2−2x−1=0 有两个不相等的实数根,则二次项系数 a 的取值范围是
A. a>1B. a>−2
C. a>1 且 a≠0D. a>−1 且 a≠0
5. 如图,线段 AB 两个端点的坐标分别为 A6,6,B8,2,以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 12 后得到线段 CD,则端点 C 的坐标为
A. 3,3B. 4,3C. 3,1D. 4,1
6. 某公司 2018 年 10 月份的生产成本是 400 万元,由于改进技术,生产成本逐月下降,12 月份的生产成本是 361 万元.若该公司这两月每个月生产成本的下降率都相同,则每个月生产成本的下降率是
A. 12%B. 9%C. 6%D. 5%
7. 一个不透明的口袋中有三个完全相同的小球,把它们分别标号为 1,2,3,随机摸出一个小球,然后放回,再随机摸出一个小球,两次摸出的小球标号的和为 5 的概率是
A. 16B. 29C. 13D. 12
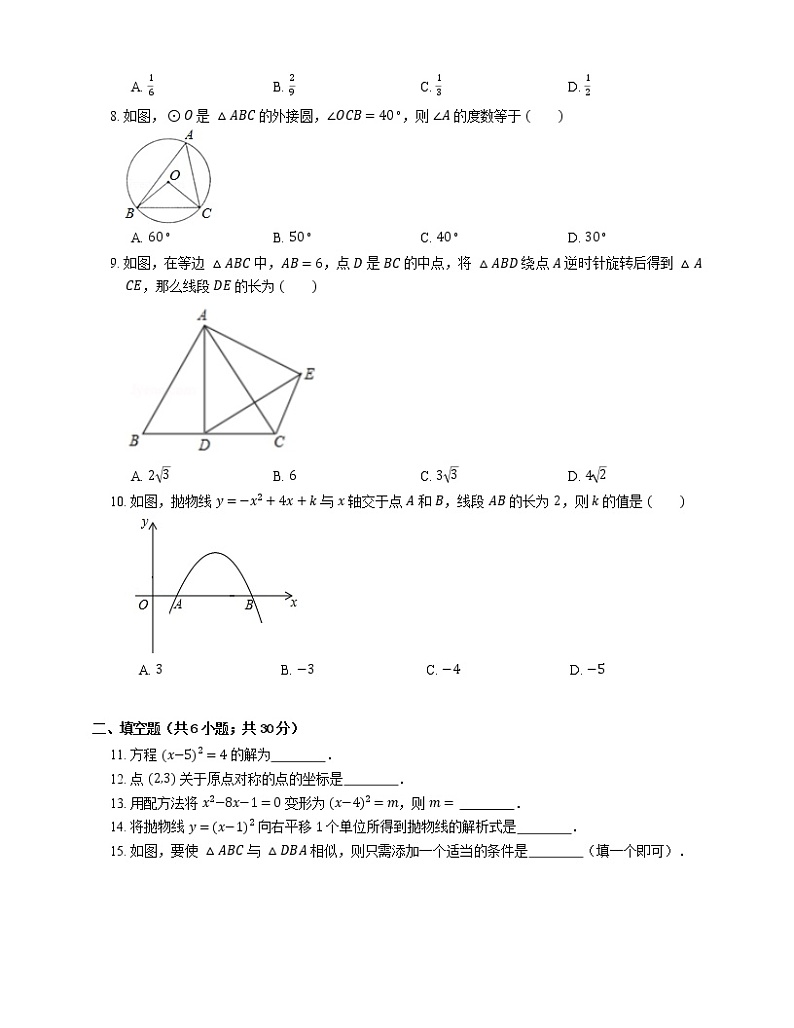
8. 如图,⊙O 是 △ABC 的外接圆,∠OCB=40∘,则 ∠A 的度数等于
A. 60∘B. 50∘C. 40∘D. 30∘
9. 如图,在等边 △ABC 中,AB=6,点 D 是 BC 的中点,将 △ABD 绕点 A 逆时针旋转后得到 △ACE,那么线段 DE 的长为
A. 23B. 6C. 33D. 42
10. 如图,抛物线 y=−x2+4x+k 与 x 轴交于点 A 和 B,线段 AB 的长为 2,则 k 的值是
A. 3B. −3C. −4D. −5
二、填空题(共6小题;共30分)
11. 方程 x−52=4 的解为 .
12. 点 2,3 关于原点对称的点的坐标是 .
13. 用配方法将 x2−8x−1=0 变形为 x−42=m,则 m= .
14. 将抛物线 y=x−12 向右平移 1 个单位所得到抛物线的解析式是 .
15. 如图,要使 △ABC 与 △DBA 相似,则只需添加一个适当的条件是 (填一个即可).
16. 如图,在 △ABC 中,∠ABC=90∘,AB=6,BC=8,∠BAC,∠ACB 的平分线相交于点 E,过点 E 作 EF∥BC 交 AC 于点 F,则 EF 的长为 .
三、解答题(共9小题;共117分)
17. 解答下列问题.
(1)解方程:xx−2+x−2=0;
(2)用配方法解方程:x2−10x+22=0.
18. 如图,平面直角坐标系中,A,B,C 坐标分别是 −2,−4,0,−4,1,−1.将 △ABC 绕点 O 逆时针方向旋转 90∘ 后得到 △AʹBʹCʹ.
(1)画出 △AʹBʹCʹ,并写出 Aʹ,Bʹ,Cʹ 的坐标;
(2)画出 △ABC 关于原点 O 对称的 △A1B1C1;
(3)以 O 为圆心,OA 为半径画圆,求扇形 OAʹA1 的面积.
19. 画出函数 y=12x−62+3 的图象,写出它的开口方向,对称轴和顶点,并说明当 y 随 x 的增大而增大时,x 的取值范围.
20. 如图,D,E 分别是 ⊙O 两条半径 OA,OB 的中点,AC=CB.
(1)求证:CD=CE.
(2)若 ∠AOB=120∘,OA=x,四边形 ODCE 的面积为 y,求 y 与 x 的函数关系式.
21. 有甲、乙两个不透明的布袋,甲袋中装有 3 个完全相同的小球,分别标有数字 0,1,2,乙袋中装有 3 个完全相同的小球,分别标有数字 −1,−2,0;现从甲袋中随机抽取一个小球,记录标有的数字为 x,再从乙袋中随机抽取一个小球,记录标有的数字为 y,确定点 M 坐标为 x,y.
(1)用树状图或列表法列举点 M 所有可能的坐标;
(2)求点 Mx,y 在函数 y=−x+1 的图象上的概率;
(3)在平面直角坐标系 xOy 中,⊙O 的半径是 2,求过点 Mx,y 能作 ⊙O 的切线的概率.
22. 如图,一块材料的形状是锐角三角形 ABC,边 BC=120 mm,高 AD=80 mm,把它加工成矩形零件,使矩形的一边在 BC 上,其余两个顶点分别在 AB,AC 上,设 EG=x mm,EF=y mm.
(1)写出 x 与 y 的关系式;
(2)用 S 表示矩形 EGHF 的面积,某同学说当矩形 EGHF 为正方形时 S 最大,这个说法正确吗?说明理由,并求出 S 的最大值.
23. 如图 1,⊙O 的半径 r=253,弦 AB,CD 交于点 E,C 为弧 AB 的中点,过 D 点的直线交 AB 延长线于点 F,且 DF=EF.
(1)试判断 DF 与 ⊙O 的位置关系,并说明理由;
(2)如图 2,连接 AC,若 AC∥DF,BE=35AE,求 CE 的长.
24. 如图,在 △ABC 中,∠ACB=90∘,以点 B 为圆心,BC 长为半径画弧,交边 AB 与点 D,以 A 为圆心,AD 长为半径画弧,交边 AC 于点 E,连接 CD.
(1)若 ∠A=28∘,求 ∠ACD 的度数;
(2)设 BC=a,AC=b.
①线段 AD 的长是方程 x2+2ax−b2=0 的一个根吗?为什么?
②若 AD=EC,求 ab 的值.
25. 如图,已知,抛物线 y=ax2−2x 过点 A−2,5,过 A 点作 x 轴的平行线,交抛物线与另一点 C,交 y 轴与点 Q,点 Dm,5 为线段 QC 上一动点(不与 Q,C 重合),作点 Q 关于直线 OD 的对称点 P,连接 PC,PD.
(1)当点 P 落在抛物线的对称轴上时,求 △OPD 的面积;
(2)若直线 PD 交 x 轴与点 E.试探究四边形 OECD 能否为平行四边形?若能,求出 m 的值,若不能,请说明理由.
(3)设点 Ph,k.
①求 PC 取最小值时 k 的值;
②当 0
第一部分
1. C【解析】因为 x2+x=0,
所以 xx+1=0,
则 x=0 或 x+1=0,
解得:x1=0,x2=−1,
故选:C.
2. B【解析】A、不是轴对称图形,是中心对称图形,故此选项错误;
B、是轴对称图形,也是中心对称图形,故此选项正确;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、是轴对称图形,不是中心对称图形,故此选项错误.
3. A【解析】过点 O 作 OD⊥AB 于点 D,连接 OA,
∵ AB=23 cm,OD⊥AB,
∴ AD=12AB=12×23=3 cm,
在 Rt△AOD 中,OA=AD2+OD2=2cm.
4. D【解析】∵ 一元二次方程 ax2−2x−1=0 有两个不相等的实数根,
∴Δ=−22−4×a×−1>0,且 a≠0,解得:a>−1 且 a≠0.
5. A
【解析】∵ 线段 AB 的两个端点坐标分别为 A6,6,B8,2,以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 12 后得到线段 CD,
∴ 端点 C 的横坐标和纵坐标都变为 A 点的一半,
∴ 端点 C 的坐标为:3,3.
6. D【解析】设每个月生产成本的下降率为 x,
根据题意得:4001−x2=361,
解得:x1=0.05=5%,x2=1.95(舍去).
7. B【解析】根据题意,画树状图如下:
共有 9 种等可能结果,其中两次摸出的小球标号的和为 5 的有 2 种,
∴ 两次摸出的小球标号的和为 5 的概率是 29.
8. B【解析】在 △OCB 中,OB=OC(⊙O 的半径),
∴∠OBC=∠0CB(等边对等角);
∵∠OCB=40∘,∠C0B=180∘−∠OBC−∠0CB,
∴∠COB=100∘;
又 ∵∠A=12∠C0B(同弧所对的圆周角是所对的圆心角的一半),
∴∠A=50∘.
9. C【解析】∵△ABC 是等边三角形,
∴AB=BC=AC=6,∠BAC=60∘,
∵BD=DC=3,
∴AD⊥BC,
∴AD=62−32=33,
∵△ABD 绕点 A 逆时针旋转后得到 △ACE,
∴∠BAD=∠CAE,AD=AE,
∴∠DAE=∠BAC=60∘,
∴△ADE 是等边三角形,
∴DE=AD=33,
故选:C.
10. B
【解析】∵ 抛物线的对称轴为直线 =−42×−1=2,而 AB=2,
∴A1,0,B3,0,
把 A1,0 代入 y=−x2+4x+k 得 −1+4+k=0,解得 k=−3.
第二部分
11. x1=7,x2=3
【解析】x−52=4,
开方得:x−5=±2,
解得:x1=7,x2=3.
12. −2,−3
【解析】根据平面内关于原点对称的点,横坐标与纵坐标都互为相反数,
故点 2,3 关于原点对称的点的坐标是 −2,−3,
故答案为:−2,−3.
13. 17
【解析】x2−8x−1=0,
移项得:x2−8x=1,
配方得:x2−8x+16=17,即 x−42=17.
所以 m=17.
14. y=x−22
【解析】将抛物线 y=x−12 向右平移 1 个单位所得到抛物线的解析式是:y=x−1−12,即 y=x−22.
故答案是:y=x−22.
15. ∠C=∠BAD
16. 103
【解析】过 E 作 EG∥AB,交 AC 于 G,则 ∠BAE=∠AEG,
∵AE 平分 ∠BAC,
∴∠BAE=∠CAE,
∴∠CAE=∠AEG,
∴AG=EG,
同理可得,EF=CF,
∵AB∥GE,BC∥EF,
∴∠BAC=∠EGF,∠BCA=∠EFG,
∴△ABC∽△GEF,
∵∠ABC=90∘,AB=6,BC=8,
∴AC=10,
∴EG:EF:GF=AB:BC:AC=3:4:5,
设 EG=3k=AG,则 EF=4k=CF,FG=5k,
∵AC=10,
∴3k+5k+4k=10,
∴k=56,
∴EF=4k=103.
故答案为:103.
第三部分
17. (1)
∵xx−2+x−2=0.∴x−2x+1=0.
则
x−2=0 或 x+1=0.
解得:
x1=2,x2=−1.
(2)
∵x2−10x+22=0.∴x2−10x+25−3=0.
则
x2−10x+25=3.
即
x−52=3.∴x−5=±3.∴x=5±3.
即
x1=5+3,x2=5−3.
18. (1) 如图所示,△AʹBʹCʹ 即为所求,Aʹ4,−2,Bʹ4,0,Cʹ1,1.
(2) 如图所示,△A1B1C1 即为所求;
(3) 由勾股定理,可得 AʹO2=20,
∴ 扇形 OAʹA1 的面积 =90×π×20360=5π.
19. 函数 y=12x−62+3 的图象如图所示:
抛物线的开口向上,对称轴为直线 x=6,顶点坐标为 6,3,
当 x>6 时,y 随 x 的增大而增大.
20. (1) 证明:连接 OC,
因为 AC=CB,
所以 ∠COA=∠COB,
因为 D,E 分别是 ⊙O 两条半径 OA,OB 的中点,
所以 OD=OE,
在 △COD 和 △COE 中,
OD=OE,∠COD=∠COE,OC=OC,
所以 △COD≌△COESAS
所以 CD=CE;
(2) 连接 AC,
因为 ∠AOB=120∘,
所以 ∠AOC=60∘,又 OA=OC,
所以 △AOC 为等边三角形,
因为点 D 是 OA 的中点,
所以 CD⊥OA,OD=12OA=12x,
在 Rt△COD 中,CD=OD⋅tan∠COD=32x,
所以四边形 ODCE 的面积为 y=12×OD×CD×2=34x2.
21. (1) 画树状图:
共有 9 种等可能的结果数,它们是:0,−1,0,−2,0,0,1,−1,1,−2,1,0,2,−1,2,−2,2,0;
(2) 在直线 y=−x+1 的图象上的点有:1,0,2,−1,
所以点 Mx,y 在函数 y=−x+1 的图象上的概率 =29;
(3) 在 ⊙O 上的点有 0,−2,2,0,在 ⊙O 外的点有 1,−2,2,−1,2,−2,
所以过点 Mx,y 能作 ⊙O 的切线的点有 5 个,
所以过点 Mx,y 能作 ⊙O 的切线的概率 =59.
22. (1) 易得四边形 EGDK 为矩形,则 KD=EG=x,
∴AK=AD−DK=80−x,
∵EF∥BC,
∴△AEF∽△ABC,
∴EFBC=AKAD,即 y120=80−x80,
∴y=−32x+1200
S=xy=−32x2+120x=−32x−402+2400,
当 x=40 时,S 有最大值 2400,
此时 y=−32×40+120=60,
即矩形 EGHF 的长为 60 mm,宽为 40 mm 时,矩形 EGHF 的面积最大,最大值为 2400 mm2,此时矩形不为正方形,
所以这个同学的说法错误.
23. (1) 如图 1,连接 OC,OD;C 为弧 AB 的中点,
因为 C 为弧 AB 的中点,
所以 OC⊥AB,∠OCE+∠AEC=90∘;
所以 DF=EF,
所以 ∠FDE=∠FED=∠AEC;
因为 OA=OC,
所以 ∠OCE=∠ODC,
所以 ∠ODC+∠CDF=90∘,
即 OD⊥DF,
所以 DF 与 ⊙O 相切.
(2) 如图 2,连接 OA,OC;
由(1)知 OC⊥AB,
所以 AH=BH;
因为 AC∥DF,
所以 ∠ACD=∠CDF;而 EF=DF,
所以 ∠DEF=∠CDF=∠ACD,
所以 AC=AE;
设 AE=5λ,则 BE=3λ,
所以 AH=4λ,HE=λ,AC=AE=5λ;
由勾股定理得:CH=3λ;CE2=CH2+HE2=9λ2+λ2,
所以 CE=10λ;
在直角 △AOH 中,由勾股定理得:
AO2=AH2+OH2,
即 r2=r−3λ2+4λ2,
解得:λ=625r=625×253=2,
所以 CE=210.
24. (1) ∵∠ACB=90∘,∠A=28∘,
∴∠B=62∘,
∵BD=BC,
∴∠BCD=∠BDC=59∘,
∴∠ACD=90∘−∠BCD=31∘.
(2) ①由勾股定理得,AB=AC2+BC2=a2+b2,
∴AD=a2+b2−a,
解方程 x2+2ax−b2=0 得,x=−2a±4a2+4b22=±a2+b2−a,
∴ 线段 AD 的长是方程 x2+2ax−b2=0 的一个根;
② ∵AD=AE,
∴AE=EC=b2,
由勾股定理得,a2+b2=12b+a2,
整理得,ab=34.
25. (1) 把点 A−2,5 代入抛物线 y=ax2−2x,得 5=4a+4,
∴a=14,
∴y=14x2−2x,
∴ 对称轴为 x=4,C10,5,
当点 P 落在抛物线的对称轴上时,如图 1,记作 Pʹ,
∴OM=4,OPʹ=OQ=5,DPʹ=DQ=m,
∴PʹM=3,PʹN=5−3=2,
在 Rt△DPN 中,m2=22+4−m2,解得 m=52,
∴△OPʹD的面积=△OQD的面积=12×5×52=254.
(2) ∵AC∥OE,
∴ 当 DC=OE 时,四边形 OECD 为平行四边形,
∵∠DOE=∠ODQ=∠ODP,
∴DE=OE=CD=10−m,
∴E10−m,0,
∵Dm,5,
∴ED2=10−2m2+52=10−m2,解得 m=53 或 m=5.
∴m 的值 53 或 5.
(3) ① ∵OP=OQ=5,OC=55,
∴ 当 O,P,C 在一条直线上时,PC 最小,如图 2,此时,点 P 记作 Pʺ,
此时 PC=PʺC=55−5,
由 △DPC"∼△EPO,
得 k5−k=555−5,
解得 k=5.
②如图 3,连接 QP,作 PH⊥QC 于 H,
则 QP⊥OD,
∴∠HQP=90∘−∠OQP=∠QOD,
∵OQ=5,QD,
∴OD 边上的高为 5mm2+25,
∴QP=10mm2+25,
∴cs∠HQP=cs∠QOD,即 h10mm2+25=5m2+25,
∴h 与 m 之间的关系为 h=50mm2+25.
2018-2019学年广东省广州市番禺区七上期末数学试卷: 这是一份2018-2019学年广东省广州市番禺区七上期末数学试卷,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018-2019学年广州市番禺区八上期末数学试卷: 这是一份2018-2019学年广州市番禺区八上期末数学试卷,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019-2020学年广东省广州市番禺区九上期末数学试卷: 这是一份2019-2020学年广东省广州市番禺区九上期末数学试卷,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












