初中数学苏科版七年级上册6.5 垂直课时作业

这是一份初中数学苏科版七年级上册6.5 垂直课时作业，共7页。试卷主要包含了5《垂直》课时练习，两条直线相交所构成的四个角中等内容，欢迎下载使用。

一、选择题
1.下列各图中，过直线l外点P画l的垂线CD，三角板操作正确的是( )
2.两条直线相交所构成的四个角中：
①有三个角都相等；
②有一对对顶角互补；
③有一个角是直角；
④有一对邻补角相等．
其中能判定这两条直线垂直的有( )
A.1个 B.2个 C.3个 D.4个
3.如图，0M⊥NP，ON⊥NP，所以ON与OM重合，理由是（ ）

A.两点确定一条直线
B.经过一点有且只有一条直线与已知直线垂直
C.过一点只能作一直线
D.垂线段最短
4.如图∠BCA=90，CD⊥AB，则图中互余的角有（ ）对.

A.1 B.2 C.3 D.4
5.如图，直线AB与直线CD相交于点O，E是∠AOD内一点，OE⊥AB，∠BOD=45°，
则∠COE的度数是( )
A.125° B.135° C.145° D.155°
6.如图，OA⊥OB，若∠1=55°，则∠2的度数是( )
A.35° B.45° C.55° D.65°
7.如图,点A在直线BC外,AC⊥BC,垂足为C,AC=3,点P是直线BC上的一个动点,则AP的长不可能是 ( )
A.2.5 B.3 C.4 D.5
8.如图，已知直线AB，CD互相垂直，垂足为O ，直线EF过点O，∠DOF∶∠BOF=2∶3，则∠AOE的度数为( )
A.36° B.54° C. 48° D.42°
9.如图所示，P为直线l外一点，A，B，C三点均在直线l上，并且PB⊥l.
有下列说法：
①PA，PB，PC三条线段中，PB最短；
②线段PB的长度叫做点P到直线l的距离；
③线段AB的长度是点A到PB的距离；
④线段AC的长度是点A到PC的距离.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.P为直线m外一点，A，B，C为直线m上三点，PA=4 cm，PB=5 cm，PC=2 cm，则点P到直线m的距离( )
A.等于4 cm B.等于2 cm C.小于2 cm D.不大于2 cm
二、填空题
11.如图，直线AB，CD相交于点O，EO⊥AB，垂足为O．若∠EOD=20°，则∠COB的度数为 °．
12.已知AB⊥CD，垂足为O，EF经过点O，∠AOE=35°，则∠DOF等于_________.
13.如图所示,AO⊥OB于点O,∠AOB∶∠BOC=3∶2,则∠AOC=________度.
14.如图,BD⊥AC于D,DE⊥BC于E,若DE=9cm,AB=12cm,不考虑点与点重合的情况,则线段BD的取值范围是________.
15.如图，AC⊥BC，CD⊥AB，垂足分别是C，D.
(1)点C到直线AB的距离是线段________的长度；
(2)点B到直线AC的距离是线段________的长度.
16.已知OA⊥OC，∠AOB：∠AOC=2：3，则∠BOC的度数为_____________
三、解答题
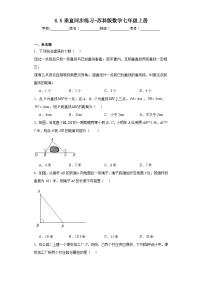
17.一辆汽车在直线形的公路上由A向B行驶,M,N分别是位于公路AB两侧的学校,如图所示.
(1)汽车在公路上行驶时,会对两个学校的教学都造成影响,当汽车行驶到何处时,分别对两个学校的影响最大?在图上标出来.
(2)当汽车从A向B行驶时,在哪一段上对两个学校的影响越来越大?哪一段上对M学校的影响逐渐减小,而对N学校的影响逐渐增大?
18.如图，O为直线AB上一点，∠AOC=eq \f(1,3)∠BOC，OC是∠AOD的平分线.
(1)求∠COD的度数；
(2)判断OD与AB的位置关系，并说明理由.
19.如图，直线AB，CD相交于点O，OM⊥AB，NO⊥CD.
(1)若∠1=∠2，求∠AOD的度数；
(2)若∠1=eq \f(1,4)∠BOC，求∠2和∠MOD的度数.
20.如图所示，直线AB、CD相交于O，OE平分∠AOD，OF⊥CD于点O，∠1=40°.
求∠2和∠3的度数.
参考答案
1.D
2.D
3.B
4.B
5.B
6.A
7.A.
8.B
9.C
10.D
11.答案为：110．
12.答案为：55°或125°；
13.答案为：150
14.答案为：9cm15.答案为：(1)CD (2)BC
16.答案为：30°或150°
17.解：(1)如图,作MC⊥AB于点C,ND⊥AB于点D,
根据垂线段最短,
所以在点C处对M学校的影响最大,在点D处对N学校的影响最大.
(2)由A向点C行驶时,对两个学校的影响逐渐增大;
由点C向点D行驶时,对M学校的影响逐渐减小,对N学校的影响逐渐增大.
18.解：(1)设∠AOC=x°，则∠BOC=3x°，
所以x°＋3x°=180°，则x=45°.
又OC平分∠AOD，
所以∠COD=∠AOC=45°
(2)OD⊥AB，理由：
由(1)知∠AOD=∠AOC＋∠COD=45°＋45°=90°，
所以OD⊥AB
19.解：∵OM⊥AB，NO⊥CD，
∴∠BOM=∠AOM=∠NOD=∠CON=90°.
(1)∵∠1=∠2，∴∠1=∠2=45°，
∴∠AOD=180°－∠2=180°－45°=135°，
即∠AOD的度数是135°.
(2)∵∠1＋∠BOM=∠BOC，∠1=eq \f(1,4)∠BOC，
∴∠1=eq \f(1,3)∠BOM=30°，∴∠2=90°－∠1=60°.
∵∠1＋∠MOD=∠COD=180°，
∴∠MOD=180°－∠1=150°.
20.解：因为OF⊥CD
所以∠FOC=90°.
因为∠1=40°，AB为直线，
所以∠3+∠FOC+∠1=180°，
所以∠3=180°-90°-40°=50°.
因为∠3与∠AOD互补，
所以∠AOD=180°-∠3=130°，
因为OE平分∠AOD，
所以∠2=0.5∠AOD=65°.