




初中数学人教版八年级上册13.3 等腰三角形综合与测试习题ppt课件
展开解:(1)(180° – 110°) ÷ 2 = 35°,故它的另外两个角都是35°. (2)分两种情况:① 当等腰三角形的一个底角为 80° 时,那么它的另一个底角为 80°,则顶角为 180° – 80° – 80° = 20°;② 当等腰三角形的顶角为 80° 时,那么它的两个底角均为 (180° – 80°) ÷ 2 = 50°.综上可知,等腰三角形的另外两个角是 20°,80° 或 50°,50°.
1.(1)等腰三角形的一个角是110°,它的另外两个角是多少度? (2)等腰三角形的一个角是80°,它的另外两个角是多少度?
证明:∵ AD∥BC, ∴∠ADB = ∠CBD. 又∵ BD 平分∠ABC, ∴∠ABD =∠CBD. ∴∠ADB = ∠ABD. ∴ AB = AD.
2.如图,AD∥BC,BD平分∠ABC.求证AB=AD.
解:∵五角星的五个角都是顶角为 36° 的等腰三角形, ∴每个底角的度数是 (180° – 36°) ÷ 2 = 72°. ∴∠AMB = 180° – 72° = 108°.
3.如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出 五角星,还需要知道∠AMB的度数,算一算∠AMB等于多少度.
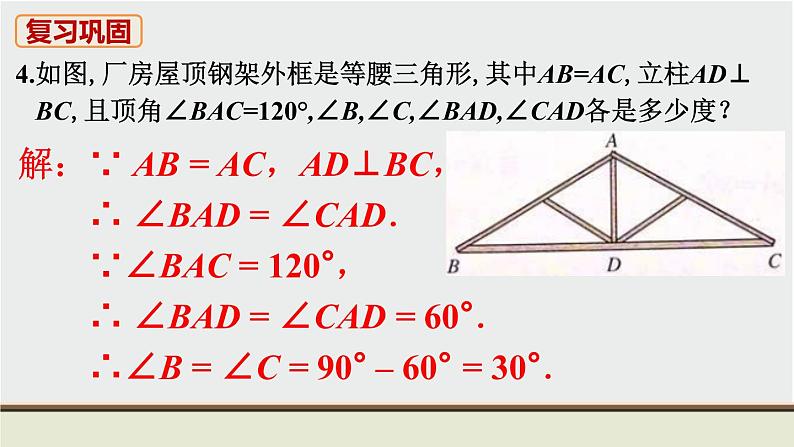
解:∵ AB = AC,AD⊥BC, ∴ ∠BAD = ∠CAD. ∵∠BAC = 120°, ∴ ∠BAD = ∠CAD = 60°. ∴∠B = ∠C = 90° – 60° = 30°.
4.如图,厂房屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥ BC,且顶角∠BAC=120°,∠B,∠C,∠BAD,∠CAD各是多少度?
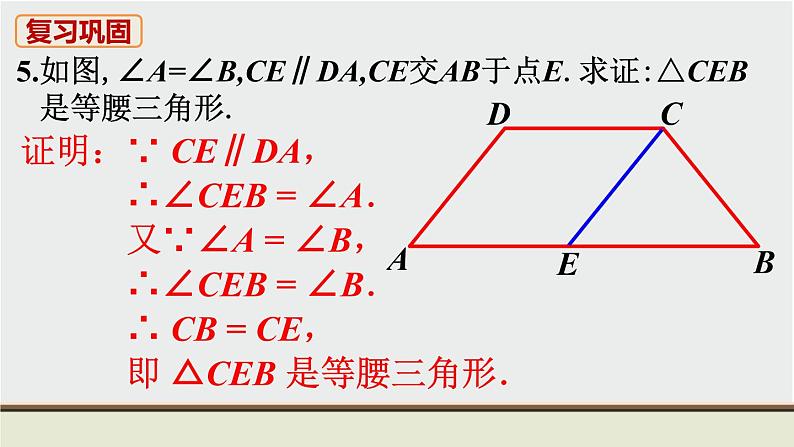
证明:∵ CE∥DA, ∴∠CEB = ∠A. 又∵∠A = ∠B, ∴∠CEB = ∠B. ∴ CB = CE, 即 △CEB 是等腰三角形.
5.如图,∠A=∠B,CE∥DA,CE交AB于点E.求证:△CEB 是等腰三角形.
证明:∵ AB = AC,AD = AE,∴ ∠B = ∠C,∠ADE = ∠AED.∴ ∠ADE – ∠B = ∠AED – ∠C,即 ∠BAD = ∠CAE.∴ △ABD ≌ △ACE (SAS).∴ BD = CE.提示:作 BC 边上的高,利用“三线合一”也可以证明结论成立.
6.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.求证BD=CE.
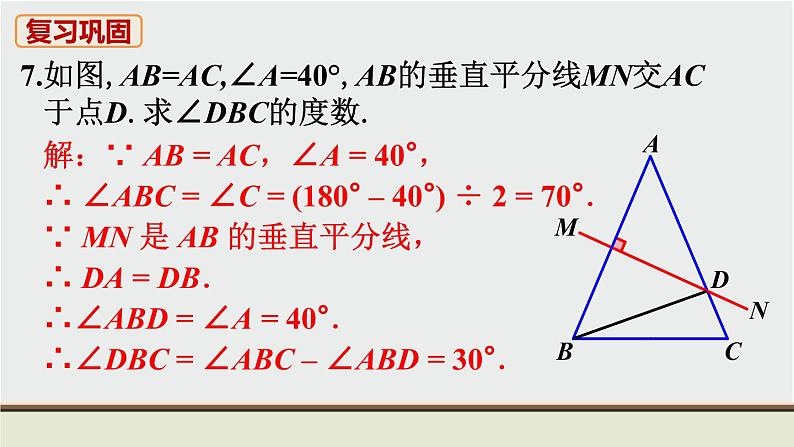
解:∵ AB = AC,∠A = 40°,∴ ∠ABC = ∠C = (180° – 40°) ÷ 2 = 70°.∵ MN 是 AB 的垂直平分线,∴ DA = DB.∴∠ABD = ∠A = 40°.∴∠DBC = ∠ABC – ∠ABD = 30°.
7.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC 于点D.求∠DBC的度数.
已知:如图,点 P 是直线 AB 上一点,求作直线 CD,使 CD⊥AB 于点 P.
8.尺规作图:经过已知直线上的一点作这条直线的垂线.
答:他们的判断是对的.因为等腰三角形底边上的中线和底边上的高重合.
9.某地地震过后,河沿村中学的同学用下面的方法检测教室的房 梁是否水平: 在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个 铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的 直角项点,同学们由此确信房梁是水平的,他们的判断对吗?为 什么?
证明:∵ MN∥BC,∴∠MOB = ∠OBC,∠NOC = ∠OCB. 又∵ BO 平分∠ABC,CO 平分∠ACB, ∴∠MBO = ∠OBC,∠NCO = ∠OCB. ∴∠MOB = ∠MBO,∠NOC = ∠NCO. ∴ MO = MB,NO = NC. ∴△AMN 的周长为 AM + AN + MN = AM + AN + MO + NO = AM + AN + MB + NC = AB + AC.
10.如图,△ABC中,BO平分∠ABC,CO平分 ∠ACB,MN经过点O,AB,AC相交于点 M,N,且MN∥BC.求证:△AMN的周长 等于AB+AC.
解:∵∠NAC = 42°,∠NBC = 84°, ∴∠C = ∠NBC – ∠NAC = 42°. ∴∠NAC = ∠C. ∴ BC = BA = 15×(10 – 8) = 30 (n mile), 即从海岛 B 到灯塔 C 的距离为 30 n mile.
11.上午8时,一条船从海岛A出发,以15 n mile/h (海里/时,1n mie=1852 m)的速度向正北航 行,10时到达海岛B处,从A,B望灯塔C,测 得∠NAC=42°,∠NBC=84°.求从海岛B 到灯塔C的距离.
证明:∵△ABD,△AEC 都是等边三角形, ∴ AD = AB,AC = AE,且∠BAD = ∠CAE = 60°. ∴∠BAD + ∠BAC = ∠CAE + ∠BAC,即∠CAD = ∠EAB. ∴ △CAD ≌ △EAB (SAS). ∴ BE = DC.
12.如图,△ABD,△AEC都是等边三角形,求证BE=DC.
解:等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等.若选前两个结论,则可利用全等三角形的判定与性质进行证明;若选“等腰三角形两腰上的高相等”这一结论,利用面积法进行证明(答案不唯一,具体过程略).
13.等腰三角形两底角的平分线相等吗?两腰上的中线呢?两腰上的 高呢?证明其中的一个结论.
14.如图,P,Q是△ABC的边BC上的两点,并且BP=PQ=QC=AP=AQ, 求∠BAC的度数.
人教版八年级上册第十五章 分式15.3 分式方程习题课件ppt: 这是一份人教版八年级上册第十五章 分式15.3 分式方程习题课件ppt,共10页。PPT课件主要包含了解下列方程,解方程求x等内容,欢迎下载使用。
人教版八年级上册15.2 分式的运算综合与测试习题课件ppt: 这是一份人教版八年级上册15.2 分式的运算综合与测试习题课件ppt,共18页。
2020-2021学年15.1 分式综合与测试习题课件ppt: 这是一份2020-2021学年15.1 分式综合与测试习题课件ppt,共14页。













