2023八年级数学上册第十三章轴对称专项2构造等腰三角形的辅助线作法作业课件新版新人教版

这是一份2023八年级数学上册第十三章轴对称专项2构造等腰三角形的辅助线作法作业课件新版新人教版，共11页。

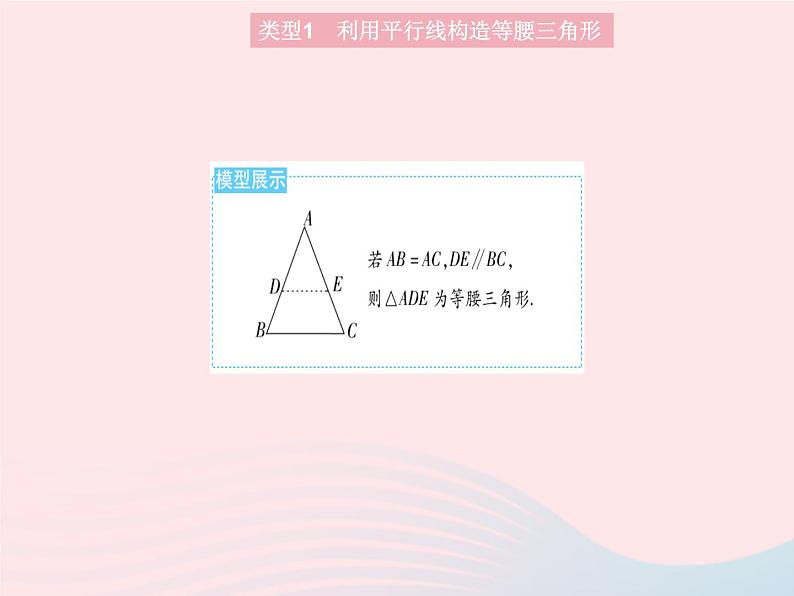
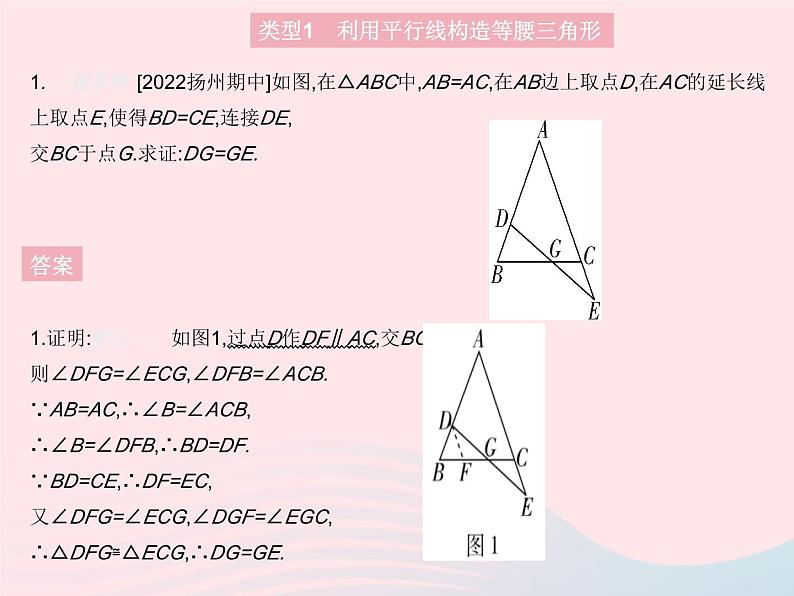
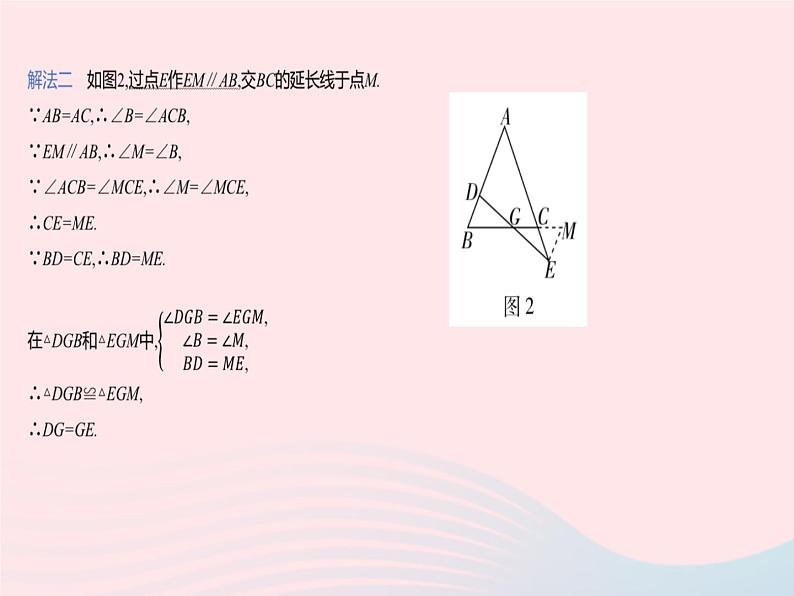
专项2　构造等腰三角形的辅助线作法类型1　利用平行线构造等腰三角形1. 一题多解 [2022扬州期中]如图,在△ABC中,AB=AC,在AB边上取点D,在AC的延长线上取点E,使得BD=CE,连接DE,交BC于点G.求证:DG=GE.类型1　利用平行线构造等腰三角形答案1.证明:解法一　如图1,过点D作DF∥AC,交BC于点F,则∠DFG=∠ECG,∠DFB=∠ACB.∵AB=AC,∴∠B=∠ACB,∴∠B=∠DFB,∴BD=DF.∵BD=CE,∴DF=EC,又∠DFG=∠ECG,∠DGF=∠EGC,∴△DFG≌△ECG,∴DG=GE. 2. 如图,△ABC是等边三角形,D是AC边上一点,DE∥AB,并交BC于点E.(1)求证:△CDE是等边三角形.(2)连接BD,延长BC至点F,使得FD=BD.求证:AD=CF.类型1　利用平行线构造等腰三角形答案2.证明:(1)∵△ABC是等边三角形,∴∠A=∠ABC=∠ACB=60°.∵DE∥AB,∴∠CDE=∠A=60°,∠DEC=∠ABC=60°,∴∠CDE=∠DEC=∠DCE=60°,∴△CDE是等边三角形. 类型2　转化倍角,构造等腰三角形3. 徐老师给爱好学习的小敏和小洁提出这样一个问题:如图1,在△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC. 小敏的证明思路:在AC上截取AE=AB,连接DE.(如图2)小洁的证明思路:延长CB至点E,使BE=AB,连接AE.(如图3)请你任意选择一种思路完成证明.类型2　转化倍角,构造等腰三角形 答案小洁的证明思路:如图2,延长CB至点E,使BE=AB,连接AE,则∠E=∠BAE.∵∠ABC=∠E+∠BAE,∴∠ABC=2∠E.∵∠ABC=2∠C,∴∠E=∠C,∴AE=AC,∵AD是∠BAC的平分线,∴∠BAD=∠DAC.∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE,∠BAE=∠E=∠C,∴∠ADE=∠DAE,∴AE=DE=AC,∴AB+BD=BE+BD=DE=AC.