人教版九年级上册22.1.1 二次函数复习ppt课件

这是一份人教版九年级上册22.1.1 二次函数复习ppt课件，共25页。PPT课件主要包含了二次函数知识点导航，左加右减上加下减等内容，欢迎下载使用。

1、二次函数的定义2、二次函数的图像及性质3、求抛物线解析式的三种方法4、a，b，c及相关符号的确定5、抛物线的平移6、二次函数与一元二次方程的关系7、二次函数的综合运用
定义： y=ax² ＋ bx ＋ c （ a 、 b 、 c 是常数， a ≠ 0 ） 定义要点：①a ≠ 0 ②最高次数为2 ③代数式一定是整式练习：1、y=-x²，y=2x²-2/x，y=100-5x²， y=3x²-2x³+5,其中是二次函数的有____个。
2、当m =_______时,函数y=(m+1)x - 2x+1 是二次函数？
2、二次函数的图像及性质
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
2、顶点式：已知抛物线顶点坐标（h, k），通常设解析式为_______________求出表达式后化为一般形式.
3、交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为____________________求出表达式后化为一般形式.
1、一般式：已知抛物线上的三点，通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
3、求抛物线解析式的三种方法
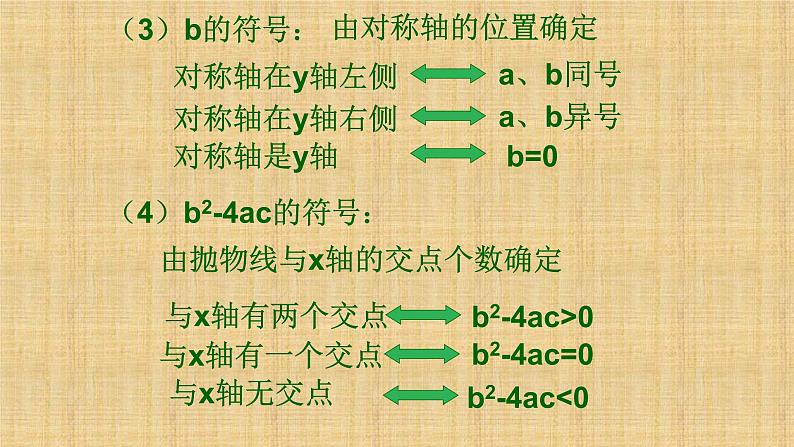
4 a，b，c及相关符号的确定
抛物线y=ax2+bx+c的符号问题：
由抛物线的开口方向确定
由抛物线与y轴的交点位置确定.
（4）b2-4ac的符号：
由抛物线与x轴的交点个数确定
１、二次函数y=ax2+bx+c(a≠0)的图象如图 所示，则a、b、c的符号为（　　） A、a<0,b>0,c>0 B、a<0,b>0,c<0 C、a<0,b<0,c>0 D、a<0,b<0,c<0
2、二次函数y=ax2+bx+c(a≠0)的图象 如图所示，则a、b、c的符号为（　　） A、a>0,b>0,c=0 B、a<0,b>0,c=0 C、a<0,b<0,c<0 D、a>0,b<0,c=0
3、二次函数y=ax2+bx+c(a≠0)的图象如图 所示，则a、b、c 、 △的符号为（ 　） A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0 C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0
熟练掌握a，b， c，△与抛物线图象的关系
(a与b：左同、右异)
4、抛物线y=ax2+bx+c(a≠0)的图象经过原点和 二、三、四象限，判断a、b、c的符号情况： a 0,b 0,c 0.
5、抛物线y=ax2+bx+c(a≠0)的图象经过原点, 且它的顶点在第三象限，则a、b、c满足 的条件是：a 0,b 0,c 0.
6、二次函数y=ax2+bx+c中，如果a>0，b<0，c<0， 那么这个二次函数图象的顶点必在第 象限
先根据题目的要求画出函数的草图，再根据图象以及性质确定结果（数形结合的思想）
练习⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象；二次函数y=2x2的图象向 平移 个单位可得到y=2(x-3)2的图象。⑵二次函数y=2x2的图象先向 平移 个单位，再向 平移 个单位可得到函数y=2(x+1)2+2的图象。
练习：（3）由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6
6 二次函数与一元二次方程的关系
一元二次方程根的情况与b²-4ac的关系我们知道:代数式b²-4ac对于方程的根起着关键的作用.
二次函数y=ax²＋bx＋c的图象和x轴交点的横坐标， 便是对应的一元二次方程ax²＋bx＋c=0的解。二次函数y=ax2+bx+c的图象和x轴交点有三种情况:(1)有两个交点(2)有一个交点(3)没有交点
二次函数与一元二次方程
b2 – 4ac > 0
b2 – 4ac= 0
b2 – 4ac< 0
若抛物线y=ax2+bx+c与x轴有交点,则
与x轴有两个不同的交点（x1，0）（x2，0）
有两个不相等的解x=x1，x=x2
有两个相等的解x1=x2=
练习：1、如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m =＿,此时抛物线 y=x2-2x+m与x轴有 个交点.
2、已知抛物线 y=x2–8x+c的顶点在 x轴上,则c=＿＿.
3、一元二次方程 3x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3x2+x-10与x轴的交点坐标是________________.
（-2、0）（5/3、0）
1、已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的 形状相同,顶点在直线x=1上,且顶点到x轴的距离 为5,请写出满足此条件的抛物线的解析式.
解: 抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同  a=1或-1 又顶点在直线x=1上,且顶点到x轴的距离为5,  顶点为(1,5)或(1,-5) 所以其解析式为: (1) y=(x-1)2+5 (2) y=(x-1)2-5 (3) y=-(x-1)2+5 (4) y=-(x-1)2-5
7二次函数的综合运用
2、已知二次函数y=ax2+bx+c的最大值是2，图象顶点在直线y=x+1上，并且图象经过点（3，-6）。求a、b、c。
解：∵二次函数的最大值是2∴抛物线的顶点纵坐标为2又∵抛物线的顶点在直线y=x+1上∴当y=2时，x=1 ∴顶点坐标为（ 1 ， 2）∴设二次函数的解析式为y=a(x-1)2+2又∵图象经过点（3，-6）∴-6=a (3-1)2+2 ∴a=-2∴二次函数的解析式为y=-2(x-1)2+2即： y=-2x2+4x
3、根据下列条件，求二次函数的解析式。
(1)、图象经过(0，0)， (1，-2) ， (2，3) 三点；
(2)、图象的顶点(2，3)， 且经过点(3，1) ；
(3)、图象经过(0，0)， (12，0) ，且最高点 的纵坐标是3 。
4、已知二次函数y=—x2+x-—（1）求抛物线开口方向，对称轴和顶点M的坐标。（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。（3）画出函数图象的示意图。（4）求ΔMAB的周长及面积。（5）x为何值时，y随的增大而减小，x为何值时，y有最大 （小）值，这个最大（小）值是多少？（6）x为何值时，y<0？x为何值时，y>0？
已知二次函数y=—x2+x-—（1）求抛物线开口方向，对称轴和顶点M的坐标。（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。（3）画出函数图象的示意图。（4）求ΔMAB的周长及面积。（5）x为何值时，y随的增大而减小，x为何值时，y有最大 （小）值，这个最大（小）值是多少？（6）x为何值时，y<0？x为何值时，y>0？
已知二次函数y=—x2+x-—（1）求抛物线开口方向，对称轴和顶点M的坐标。（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。（3）画出函数图象的示意图。（4）求ΔMAB的周长及面积。（5）x为何值时，y随的增大而减小，x为何值时，y有最大 （小）值，这个最大（小）值是多少？（6）x为何值时，y<0？x为何值时，y>0？
当x=-1时，y有最小值为y最小值=-2
当x≤-1时，y随x的增大而减小;