人教版七年级上册1.5.3 近似数教案

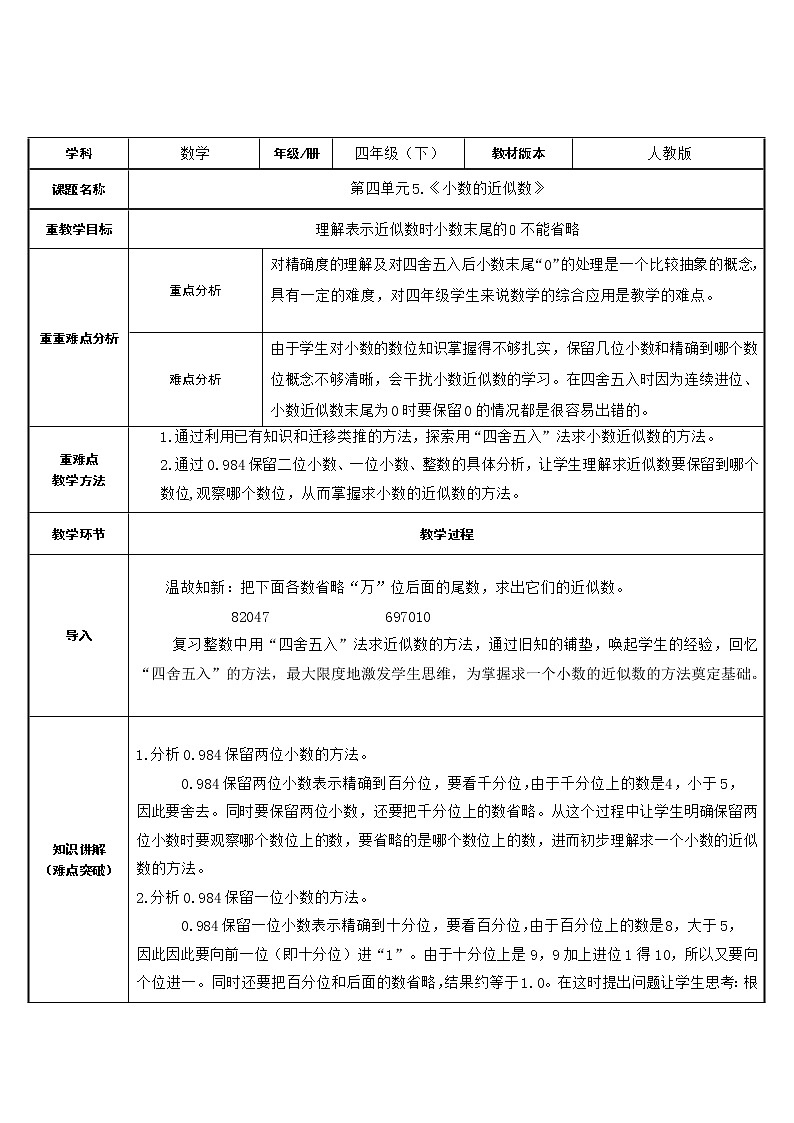
学科

数学

年级/册

四年级（下）

教材版本

人教版

课题名称

第四单元5.《小数的近似数》

重教学目标

理解表示近似数时小数末尾的0不能省略

重重难点分析

重点分析

对精确度的理解及对四舍五入后小数末尾“0”的处理是一个比较抽象的概念，具有一定的难度，对四年级学生来说数学的综合应用是教学的难点。

难点分析

由于学生对小数的数位知识掌握得不够扎实，保留几位小数和精确到哪个数位概念不够清晰，会干扰小数近似数的学习。在四舍五入时因为连续进位、小数近似数末尾为0时要保留0的情况都是很容易出错的。

重难点

教学方法

1.通过利用已有知识和迁移类推的方法，探索用“四舍五入”法求小数近似数的方法。

2.通过0.984保留二位小数、一位小数、整数的具体分析，让学生理解求近似数要保留到哪个数位,观察哪个数位，从而掌握求小数的近似数的方法。

教学环节

教学过程

导入

温故知新：把下面各数省略“万”位后面的尾数，求出它们的近似数。

82047                697010

     复习整数中用“四舍五入”法求近似数的方法，通过旧知的铺垫，唤起学生的经验，回忆“四舍五入”的方法，最大限度地激发学生思维，为掌握求一个小数的近似数的方法奠定基础。

知识讲解

（难点突破）

1.分析0.984保留两位小数的方法。

0.984保留两位小数表示精确到百分位，要看千分位，由于千分位上的数是4，小于5，

因此要舍去。同时要保留两位小数，还要把千分位上的数省略。从这个过程中让学生明确保留两位小数时要观察哪个数位上的数，要省略的是哪个数位上的数，进而初步理解求一个小数的近似数的方法。

2.分析0.984保留一位小数的方法。

    0.984保留一位小数表示精确到十分位，要看百分位，由于百分位上的数是8，大于5，

因此因此要向前一位（即十分位）进“1”。由于十分位上是9，9加上进位1得10，所以又要向个位进一。同时还要把百分位和后面的数省略，结果约等于1.0。在这时提出问题让学生思考：根据小数的性质，1.0和1的大小是相等的，那么小数末尾的0能不能去掉？

    通过分析让学生理解：1.0和1虽然大小相等，但表示的精确度是不相同的，1.0表示精确到十分位，1表示精确到个位，在表示近似数时，小数末尾的0起到“占位和表示精确度”的作用，所以0不能去掉。在这里特别指出求小数近似数的注意事项，并说明保留不同位数小数的精确程度，促使学生深入理解近似数的精确性。

3.简单分析0.984保留整数的方法。

    0.984保留整数，表示精确到个位，要看十分位，十分上的数是9，大于5，因此要向前一位也就是个位进一，，然后把十分位和后面的数省略，结果约等于1.

通过对0.984分别保留两位小数、一位小数及保留整数的分析过程，让学生明确保留到哪个数位，需要观察的是哪个数位上的数，而要省略的是哪个数位上的数，从而掌握求一个小数的近似数的方法。

课堂练习

（难点巩固）

4.通过学习0.984分别保留两位小数、一位小数及保留整数的方法，学生对求一个小数的近似数的方法已经有了一个初步的认识，这时适时的提出问题：你能总结出“四舍五入”法求小数近似数的方法吗？

让学生对求小数近似数的方法进行概括，促进学生自主探索并归纳求小数的近似数的方法。让学生在重温学习的过程中获得积极的情感体验，使知识的脉络更加清晰，更有条理。

小结

求近似数时，保留整数，要看十分位上的数；保留一位小数，要看百分位上的数；保留两位小数，要看千分位上的数……也就是看要求保留位数的后面一位上的数是否满5，满5进1，不满5舍去。保留哪位，就要把这位后面的数都省略。

注意：在表示近似数时，小数末尾的0不能去掉。

求近似数时，保留整数，表示精确到个位；保留一位小数，表示精确到十分位；保留两位小数，表示精确到百分位 ……