


- 【小单元教案】高中数学人教A版(2019)必修第一册--2.1.2 等式性质与不等式性质(课时教学设计) 教案 3 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--2.2 基本不等式(单元教学设计) 教案 4 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--2.2.2 利用基本不等式解决最值问题(课时教学设计) 教案 3 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--2.3 二次函数与一元二次方程、不等式(1)(单元教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--2.3 二次函数与一元二次方程、不等式(2)(单元教学设计) 教案 2 次下载
数学必修 第一册2.2 基本不等式公开课教案
展开![]() 2.2 基本不等式
2.2 基本不等式
第1课时 基本不等式的解释和证明
(一)教学内容
基本不等式的含义和证明。
(二)教学目标
1. 经历基本不等式的发现归纳过程,能从具体中抽象出基本不等式,体会数学的一般性,发展学生数学抽象素养。
2. 经历基本不等式的证明过程,能用分析法证明不等式,体会数学的严谨性,发展学生逻辑推理、数学运算素养。
3. 通过寻找基本不等式的几何解释,能理解基本不等式的几何直观,体会数形结合思想,发展直观想象的素养;
4. 利用基本不等式求简单的最值问题,能把握基本不等式的使用条件“一正二定三相等”,体会数学的灵活性,发展数学运算素养。
(三)教学重点及难点
1. 重点:基本不等式的定义,证明和几何解释。
2.难点:基本不等式的证明。
(四)教学过程设计
1.情境引入,提出问题
(1)欧拉与羊圈的故事:
小欧拉曾经因为星星的事情被教会学校开除,回家后无事,他就帮助爸爸放羊,成了一个牧童。他一面放羊,一面读书。他读的书中,有不少数学书。
爸爸的羊群渐渐增多了,达到了100只。原来的羊圈有点小了,爸爸决定建造一个新的羊圈。他用尺量出了一块长方形的土地,长40米,宽15米,他一算,面积正好是600平方米,平均每一头羊占地6平方米。正打算动工的时候,他发现他的材料只够围100米的篱笆,不够用。若要围成长40米,宽15米的羊圈,其周长将是110米(15+15+40+40=110)父亲感到很为难,若要按原计划建造,就要再添10米长的材料;要是缩小面积,每头羊的面积就会小于6平方米。
小欧拉却向父亲说,不用缩小羊圈,也不用担心每头羊的领地会小于原来的计划。他有办法。父亲不相信小欧拉会有办法,听了没有理他。小欧拉急了,大声说,只有稍稍移动一下羊圈的桩子就行了。
父亲听了直摇头,心想:“世界上哪有这样便宜的事情?”但是,小欧拉却坚持说,他一定能两全齐美。父亲终于同意让儿子试试看。
小欧拉见父亲同意了,站起身来,跑到准备动工的羊圈旁。他以一个木桩为中心,将原来的40米边长截短,缩短到25米。父亲着急了,说:“那怎么成呢?那怎么成呢?这个羊圈太小了,太小了。"小欧拉也不回答,跑到另一条边上,将原来15米的边长延长,又增加了10米,变成了25米。经这样一改,原来计划中的羊圈变成了一个25米边长的正方形。然后,小欧拉很自信地对爸爸说:"现在,篱笆也够了,面积也够了。”父亲照着小欧拉设计的羊圈扎上了篱笆,100米长的篱笆真的够了,不多不少,全部用光。面积也足够了,而且还稍稍大了一些。
【设计意图】讲数学家故事,渗透德育文化,激发学生数学学习兴趣和积极性。
(2)回顾上一节课的内容——“重要不等式”:
多媒体展示第24届国际数学家大会的会标,介绍赵爽弦图历史渊源。


 师生活动:我们把会标抽象成在正方形
师生活动:我们把会标抽象成在正方形![]() 中有4个全等的直角三角形,设直角三角形的两条直角边长为
中有4个全等的直角三角形,设直角三角形的两条直角边长为![]() ,那么正方形的边长为
,那么正方形的边长为![]() 。这样4个直角三角形的面积和为
。这样4个直角三角形的面积和为![]() ,正方形的面积为
,正方形的面积为![]() ,由于正方形
,由于正方形![]() 的面积大于4个直角三角形的面积和,我们就等到一个不等式
的面积大于4个直角三角形的面积和,我们就等到一个不等式
![]()
追问1:如果用![]() 代替
代替![]() ,用
,用![]() 代替
代替![]() ,得到
,得到![]() ,即
,即![]() ①,当且仅当
①,当且仅当![]() 时,等号成立。我们称不等式①为基本不等式。
时,等号成立。我们称不等式①为基本不等式。
(3)具体演算,总结规律
当![]() 分别取下列值时,基本不等式
分别取下列值时,基本不等式![]() 成立吗?
成立吗?
(1)当![]() ,(2)当
,(2)当![]() ,(3)当
,(3)当![]() 。
。
师生活动:学生亲自运算检验,体会不等式的成立。
【设计意图】利用实际问题抽象出不等式模型,在通过字母代换等到基本不等式模式,最后用具体数值验证,加深对基本不等式的认识。
教师总结:其中![]() 叫做正数
叫做正数![]() 的算术平均数,
的算术平均数,![]() 叫做正数
叫做正数![]() 的几何平均数。基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
的几何平均数。基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
【设计意图】通过分析基本不等式的结构特征得到基本不等式的代数解释,加深对基本不等式的认识,多种方法下,培养学生的发散思维。
- 公式证明,形成概念
问题2.我们通过考察![]() 的特殊情形获得了基本不等式,你能否直接利用不等式的性质推导出基本不等式呢?
的特殊情形获得了基本不等式,你能否直接利用不等式的性质推导出基本不等式呢?
师生活动:学生可能根据两个实数大小关系的基本事实,用作差比较法证明上式。教师在肯定学生的做法之后,给学生简单介绍分析法并且引导学生用分析法写出证明过程。
教师:分析法是一种“执果索因”的证明方法,即从要证明的结论出发,逐步寻求使他成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理)为止。
分析法解题过程如下:
要证 ![]() ①
①
只要证 ![]()
要证![]() ,只要证
,只要证 ![]() . ③
. ③
要证③,只要证 ![]() 0 ④
0 ④
要证④,只要证 ![]() 0 ⑤
0 ⑤
显然,⑤成立,![]() 中的等号成立。
中的等号成立。
我们可以看到,只要把上面的过程倒过来,就可以直接推出基本不等式了。
追问(1):请同学们想一想上述证明中每一步推理的依据是什么?
教师引导由②![]() ①,由③
①,由③![]() 由④
由④![]() ,由⑤
,由⑤![]() ④的依据。
④的依据。
教师总结:②![]() ①(根据不等式性质,两边同乘以一个正数,所得不等式与原不等式同向)
①(根据不等式性质,两边同乘以一个正数,所得不等式与原不等式同向)
③![]() (根据不等式性质,两边同时加上正数(
(根据不等式性质,两边同时加上正数(![]() ),所得不等式与原不等式同向)
),所得不等式与原不等式同向)
④![]() (运用完全平方差公式打开计算)
(运用完全平方差公式打开计算)
⑤![]() ④(根据不等式性质,两边同乘以一个负数,所得不等式与原不等式反向)
④(根据不等式性质,两边同乘以一个负数,所得不等式与原不等式反向)
显然,⑤成立,![]() 中的等号成立。
中的等号成立。
追问(2):上述证明方法叫做“分析法”,你能归纳一下用分析法证明命题的思路吗?
师生活动:学生讨论后回答。
教师总结:分析法是一种“执果索因”的证明方法,即从要证明的结论出发,逐步寻求使他成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理)为止。
追问(3):根据我们的证明过程,说说分析法的证明格式是怎样的?
师生活动:学生思考后回答。
教师总结:由于分析法是从要证明的结论出发,逐步寻求使它成立的充分条件,所以分析法在书写过程中必须有相应的文字说明:一般每一步的推理都用“要证……”“只要证……”的格式,当推导到一个明显成立的条件之后,指出显然……成立。
【设计意图】作差比较是学生最有可能想到的方法,但教师还是需要介绍“执果索因”的“分析法”。它从求证的不等式出发,逆向逐步探寻这个不等式成立需要具备的充分条件,其基本思想是: 由未知探索需知,逐步推向已知。在数学中,条件探究题一般用分析法进行逆推来获得正确答案,是思考问题的一般性方法。
- 几何解释,加深理解
问题3. 如图AB是圆的直径,点C是AB上一点,AC=a,BC=b,过点C做垂直于AB的弦DE,连接AD,BD,你能利用这个图形得到基本不等式的几何解释吗?
如图AB是圆的直径,点C是AB上一点,AC=a,BC=b,过点C做垂直于AB的弦DE,连接AD,BD,你能利用这个图形得到基本不等式的几何解释吗?
师:前后4人小组,4分钟时间讨论交流。
生:小组讨论,选派小组代表上台为同学展示交流成果,其他同学做补充。
师:肯定小组交流成果。
师:几何画板动态演示,使学生直观感受变与不变.师:引导学生总结,半径即为![]() ,
,![]() ,圆中直径不小于任意一条弦,当且仅当弦过圆心时,二者相等。
,圆中直径不小于任意一条弦,当且仅当弦过圆心时,二者相等。
【设计意图】学生自己发现基本不等式的几何解释相对较困难,给出几何图形后,引导学生将![]() 和
和![]() 与图中的几何元素建立起联系,再观察这些几何元素在变化中表现得大小关系,从而得到基本不等式的几何解释,几何画板演示增强视觉直观,数形结合。
与图中的几何元素建立起联系,再观察这些几何元素在变化中表现得大小关系,从而得到基本不等式的几何解释,几何画板演示增强视觉直观,数形结合。
- 例题讲解,示范巩固
前面我们知道了基本不等式的内容、证明方法和几何解释,下面我们利用基本不等式来解决一些简单的最值问题.请看下面的例题。
例1 已知![]() 的最小值。
的最小值。
追问1:本题中要求最小值的代数式有什么结构特点?是否可以利用基本不等式求![]() 的最小值?
的最小值?
师生活动:学生思考后回答。
教师总结:本题中要求的代数式是![]() 与
与![]() 和的形式,而且
和的形式,而且![]() ,由于
,由于![]() 是
是![]() 与
与![]() 的算术平均数的2倍,而后者的几何平均数
的算术平均数的2倍,而后者的几何平均数![]() 是一个定值,所以可以利用基本不等式求解。 下面是解答过程。
是一个定值,所以可以利用基本不等式求解。 下面是解答过程。
解:因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]()
因此所求的最小值是2。
追问2:在上述解答过程中,是否必须说明“当且仅当![]() ,即
,即![]() ”?
”?
师生活动:学生讨论后回答。
教师总结:这是为了说明“2”是![]() 的一个取值。那么请同学们再想一想,当
的一个取值。那么请同学们再想一想,当![]() 这时能说
这时能说![]() 是
是![]() 的最小值吗?
的最小值吗?
师生活动:学生思考后回答。
教师总结:当然是不能,因为![]() 的最小值,就是要求出一个
的最小值,就是要求出一个![]() 如果
如果![]() 。
。
追问3:通过本例的解答,你能说说满足什么条件能够利用基本不等式求最小值呢?
师生活动:学生讨论后回答。
教师总结:如果两个正数的积为定值,当这两个数相等时,可以求得它们的和的最小值。
【设计意图】引导学生根据所求代数式的形式,判断是否利用基本不等式解决问题,同时强调代数式的最值必须是代数式能取到的值,为学生求解代数式的最值问题提供示范(模型)。
5.基础训练,检测评价
练习1.已知![]()
![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.1 B.2 C.4 D.8
练习2.已知![]() 且
且![]() ,则
,则![]() 的最大值为( )
的最大值为( )
-
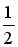 B.1 C.2 D.4
B.1 C.2 D.4
练习3.已知![]() ,求
,求![]() 的最大值?
的最大值?
师:最小值的含义是什么?
学生思考后回答,教师总结,即求一个实数M,使所有值都大于等于M,并且能取到M。
生:第一题可以利用基本不等式求得,首先满足应用条件![]() 代入公式,求得
代入公式,求得![]() ,当且仅当
,当且仅当![]() =1时等号成立。
=1时等号成立。
师:引导学生在该题的基础之上,对基本不等式进行变形,得到![]() ,总结得到“两个正数积定和最小”。
,总结得到“两个正数积定和最小”。
生:第二题符合基本不等式应用条件,代入公式求得![]() ,当且仅当
,当且仅当![]() =1时等号成立。
=1时等号成立。
师:引导学生对基本不等式进行变形得 ,总结得到“两个正数和定积最大”。
,总结得到“两个正数和定积最大”。
生:分析基本不等式的应用前提,即两个正数,将![]() ,看作两个整体,要求a,b同号。
,看作两个整体,要求a,b同号。
师:第三题是第二题的延伸拓展,能否用第二题的思路解决?
【设计意图】通过本例的教学,可以帮助学生理解如何直接应用基本不等式解决问题,设置三个题目,逐渐强化基本不等式的应用条件,并由学生亲自发现和总结公式变形,形成求解最值问题的数学模型,进一步发展模型思想,整体思想.由题目出发,总结易错和注意事项,加深学生对于基本不等式理解,增加学生获得感,满足感。
- 凝炼模型,总结升华
例2已知![]() 都是正数,求证:
都是正数,求证:
(1)如果积![]() 等于定值
等于定值![]() ,那么当
,那么当![]() 时,和
时,和![]() ;
;
(2)如果和![]() 等于定值
等于定值![]() , 那么当
, 那么当![]() 时,积
时,积![]() .
.
师生活动:师生一起分析后,鼓励学生用自然语言把两个问题连在一起说,能用自己的话表达也是对结论的进一步理解。并书写证明过程后展示,师生共同补充完善。
证明:(1)因为![]() 都是正数,所以
都是正数,所以![]() , 当积
, 当积![]() 等于定值
等于定值![]() 时,
时,![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 和
和![]() ;
;
(2)当和![]() 等于定值
等于定值![]() 时,
时,![]() =
=![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,
,![]()
追问:通过本题,你能说说用基本不等式能够解决什么样的问题吗?
师生活动:学生思考后回答。
教师总结:满足两个正数的积为定值,当这两个数取什么值时,求它们的和的最小值,或者两个正数的和为定值,当这两个数取什么值时,求它们的积的最大值的问题,能够用基本不等式解决。
【设计意图】通过问题链的解决,引导学生认识基本不等式“和式”与“积式”的转化功能,归纳和提炼出最值定理.“模式识别”能起到定向训练的作用,即训练学生在遇到新问题时,善于识别问题的特征,准确地将其归结为某种数学模型,尽快地明确解题思路,选择解题方法。
- 归纳小结
(1)什么是基本不等式?如何推导得到基本不等式?
(2)基本不等式的代数特征是什么?如何从几何图形上解释?
(3)基本不等式的使用条件是什么?如何利用基本不等式解决最值问题?需要注意什么?
(4)本节课有哪些数学思想方法?
师:引导同学们相互总结本节课的收获和注意事项。
生:踊跃发言,从知识层面和思想方法两个角度总结本节课内容。
【设计意图】引导学生回顾总结学习内容和方法,梳理课堂内容,形成知识框架和思想方法体系。特別要注意引导学生会研究一个特殊代数对象的一般过程。
- 作业布置:课本习题2.2 第1题,第2题
【设计意图】巩固新知,强化基础,选择性内容满足不同学生发展需求,限时完成强化学习效率。
(五)目标检测设计
1.已知![]() ,求
,求![]() 的最小值及相应的
的最小值及相应的![]() 值。
值。
2.已知![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 值。
值。
【设计意图】考查学生利用基本不等式解决简单的最值问题的能力。
(六)教学反思
由国际数学家大会的会标引出,让学生具体数值演算验证,有助于增强学生学习信心;讲好基本不等式的几何解释,有助于培养学生的直观想象和感受数学魅力;作为基本不等式的第一课时,不能急于求成,本节课重在理解好基本不等式的含义,做好扎实证明,例题也只讲最基本的,对于使用条件,不要强塞硬给,让学生在后续学习中,慢慢体会和掌握。
人教A版 (2019)必修 第一册4.3 对数优秀教案设计: 这是一份人教A版 (2019)必修 第一册4.3 对数优秀教案设计,共4页。
高中人教A版 (2019)4.1 指数一等奖教案设计: 这是一份高中人教A版 (2019)4.1 指数一等奖教案设计,共5页。
【小单元教案】高中数学人教A版(2019)必修第一册--3.1.1 函数的概念(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--3.1.1 函数的概念(课时教学设计),共8页。













