




人教版九年级上册24.1.1 圆课时作业
展开
课后巩固
一.选择题(共8小题)
1.如图所示圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2cm,若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆的直径是( )
A.1cm B.2cm C.4cm D.πcm
【分析】根据圆的认识进行解答即可.
【解答】解:∵AB=2cm,
∴圆的直径是4cm,
故选:C.
【点评】此题考查圆的认识,关键是根据圆的概念进行解答.
2.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
【分析】利用半径相等得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=∠AOC进行计算即可.
【解答】解:连结OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
【点评】本题考查了圆的认识:掌握与圆有关的概念( 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
3.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.
其中错误说法的个数是( )
A.1 B.2 C.3 D.4
【分析】根据弦的定义、弧的定义、以及确定圆的条件即可解决.
【解答】解:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
【点评】本题考查弦与直径的区别,弧与半圆的区别,及确定圆的条件,不要将弦与直径、弧与半圆混淆.
4.如图,一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是( )
A.4πr B.2πr C.πr D.2r
【分析】一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离就是圆的周长.
【解答】解:圆心经过的距离就是圆的周长,所以是2πr.
故选:B.
【点评】考查了圆的认识,本题的关键是明白圆心经过的距离就是圆的周长,然后利用周长公式求.
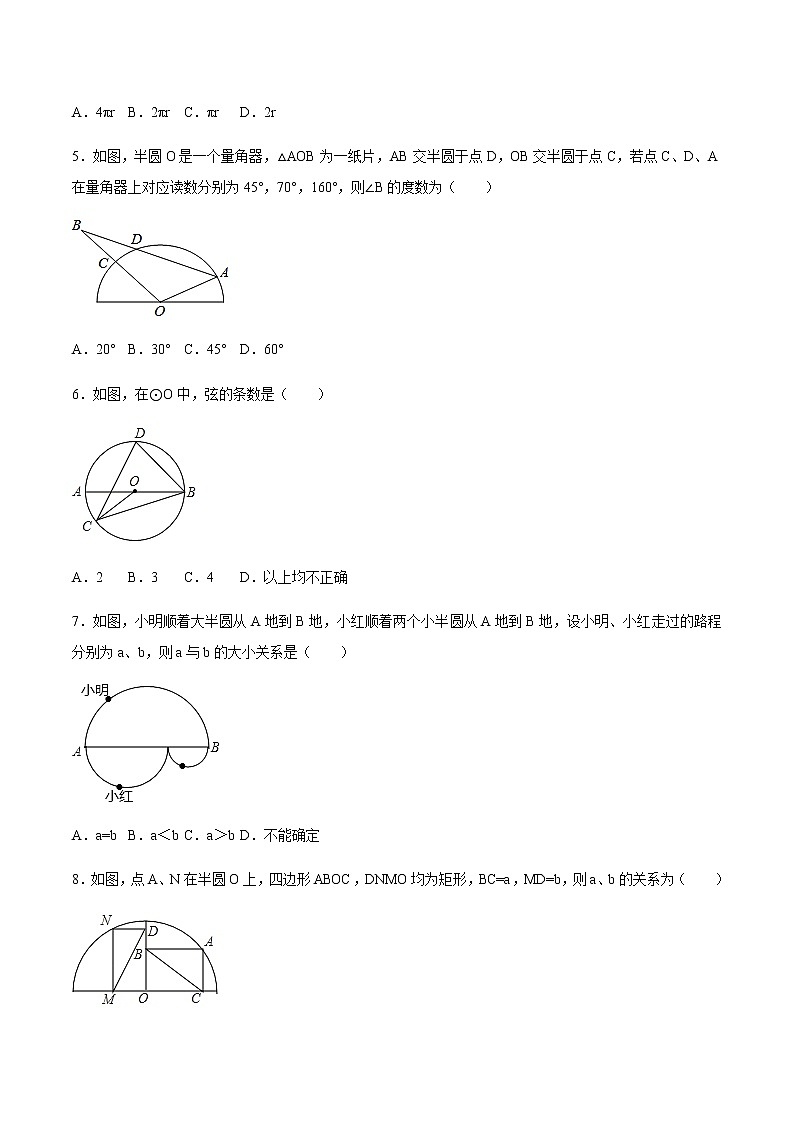
5.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B的度数为( )
A.20° B.30° C.45° D.60°
【分析】连结OD,如图,根据题意得∠DOC=25°,∠AOD=90°,由于OD=OA,则∠ADO=45°,然后利用三角形外角性质得∠ADO=∠B+∠DOB,所以∠B=45°﹣25°=20°.
【解答】解:连结OD,如图,则∠DOC=70°﹣45°=25°,∠AOD=160°﹣70°=90°,
∵OD=OA,
∴∠ADO=45°,
∵∠ADO=∠B+∠DOB,
∴∠B=45°﹣25°=20°.
故选:A.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
6.如图,在⊙O中,弦的条数是( )
A.2 B.3 C.4 D.以上均不正确
【分析】根据弦的定义进行分析,从而得到答案.
【解答】解:如图,在⊙O中,有弦AB、弦DB、弦CB、弦CD.共有4条弦.
故选:C.
【点评】本题考查了圆的认识.连接圆上任意两点的线段叫弦,理解弦的定义是解决本题的关键.
7.如图,小明顺着大半圆从A地到B地,小红顺着两个小半圆从A地到B地,设小明、小红走过的路程分别为a、b,则a与b的大小关系是( )
A.a=b B.a<b C.a>b D.不能确定
【分析】根据图形,得两个小半圆的直径之和等于大半圆的直径,则根据圆周长公式,得二人所走的路程相等.
【解答】解:设小明走的半圆的半径是R.则小明所走的路程是:πR.
设小红所走的两个半圆的半径分别是:r1与r2,则r1+r2=R.小红所走的路程是:πr1+πr2=π(r1+r2)=πR.因而a=b.
故选:A.
【点评】本题考查了圆的认识,注意计算两个小半圆周长的时候,可以提取,则两个小半圆的直径之和是大半圆的直径.
8.如图,点A、N在半圆O上,四边形ABOC,DNMO均为矩形,BC=a,MD=b,则a、b的关系为( )
A.a>b B.a=b C.a<b D.a≤b
【分析】连结ON、OA,如图,利用圆的半径相等得到ON=OA,再根据矩形的性质得ON=MD,OA=BC,则有BC=MD.
【解答】解:连结ON、OA,如图,
∵点A、N在半圆上,
∴ON=OA,
∵四边形ABOC,DNMO均为矩形,
∴ON=MD,OA=BC,
∴BC=MD,即a=b.
故选:B.
【点评】本题考查了圆的认识:与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了矩形的性质.
二.填空题(共4小题)
9.如图,在⊙O中,点A、O、D和点B、O、C分别在一条直线上,图中共有 三 条弦,它们分别是 AE,DC,AD .
【分析】根据弦的定义进行分析,从而得到答案.
【解答】解:图中的弦有AE,DC,AD共三条,
故答案为:三,AE,DC,AD.
【点评】本题考查圆的认识,理解弦的定义是解决本题的关键.
10.下列说法中正确的个数是 2 .
(1)长度相等的两条弧是等弧;
(2)半径相等的两个半圆是等弧;
(3)同圆中,优弧与劣弧的和等于一个整圆;
(4)分别在两个等圆上两条弧是等弧;
(5)能够完全重合的弧是等弧.
【分析】利用圆的有关定义及性质分别判断后即可确定正确的答案.
【解答】解:(1)长度相等的两条弧是等弧,错误;
(2)半径相等的两个半圆是等弧,正确;
(3)同圆中,优弧与劣弧的和等于一个整圆,错误;
(4)分别在两个等圆上两条弧是等弧,错误;
(5)能够完全重合的弧是等弧,正确,
正确的有2个,
故答案为2.
【点评】本题考查了圆的认识,解题的关键是了解圆的有关性质及定义,属于基础定义,比较简单.
11.如图,AB,CD是⊙O的两条相交弦,图中共有 6 条劣弧,共有 3 条优弧.
【分析】根据大于半圆的弧为优弧、小于半圆的弧为劣弧进行判断可得出答案.
【解答】解:
∵AB、CD是小于直径的弦,
∴、是小于半圆的弧,、是大于半圆的弧,
∴、、、是小于半圆的弧,是大于半圆的弧,
∴劣弧有6条,优弧有3条,
故答案为:6;3.
【点评】本题主要考查圆的认识,掌握大于半圆的弧为优弧、小于半圆的弧为劣弧是解题的关键.
12.如图,AB是O的直径,设AB=a,那么⊙O的周长l=πa,有一个小圆的直径在线段AB上且与⊙O只有一个公共点A,现将这一小圆点向B方向平移,恰好平移1次后与⊙O只有一个公共点B,则此时小圆的周长是 πa ;若仿照上述方法,小圆恰好平移2次也有同样的结果,则此时小圆的周长是 πa ;若仿照上述方法恰好平移n次也有同样的结果,则此时小圆的周长是 πa .
【分析】先求出平移后小圆的直径,然后根据圆的周长公式计算相应小圆的周长即可.
【解答】解:若将小圆点向B方向平移,恰好平移1次后与⊙O只有一个公共点B,小圆的直径为a,所以此时小圆的周长是πa;
若仿照上述方法,小圆恰好平移2次也有同样的结果,则此时小圆的周长是πa;
若仿照上述方法恰好平移n次也有同样的结果,则此时小圆的周长是πa.
故答案为πa,πa,πa.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
三.解答题(共4小题)
13.如图,已知AB,CB为⊙O的两条弦,请写出图中所有的弧.
【分析】根据弧的定义进行解答即可.
【解答】解:图中的弧为.
【点评】此题考查圆的认识,关键是根据弧的定义解答.
14.已知;如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
【分析】首先证明OC=OD,再证明△OCB≌△ODA,进而得到AD=BC.
【解答】解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
【点评】此题主要考查了圆的认识,以及全等三角形的判定,关键是掌握全等三角形的判定方法:SSS、ASA、SAS、AAS.
15.如图,直线AB经过⊙O的圆心,与⊙O相交于点A、B,点C在⊙O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与⊙O相交于点Q,问:点P在直线AB的什么位置上时,QP=QO?这样的点P共有几个?并相应地求出∠OCP的度数.
【分析】点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
【解答】解:①根据题意,画出图①,
在△QOC中,OC=OQ,
∴∠OQC=∠OCQ,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图②)
∵OC=OQ,∴∠OQP=①,
∵OQ=PQ,
∴∠OPQ=②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图③),
∵OC=OQ,
∴∠OCP=∠OQC=①,
∵OQ=PQ,
∴∠P=②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
综上所述,∠OCP=180°﹣150°﹣10°=20°.
【点评】考查了圆的认识和等腰三角形的性质,注意:分三种情况进行讨论是解决本题的关键.
16.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
【分析】分别连接ME、MF,根据直角三角形中,斜边上的中线等于斜边的一半可得到ME=MD=MC=MB,可证得结论.
【解答】证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
【点评】本题主要考查直角三角形的性质,根据直角三角形中斜边上的中线等于斜边的一半得到ME=MF=MC=MB是解题的关键.
课堂测试
1.在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合”.由此说明( )
A.圆的直径互相平分
B.垂直弦的直径平分弦及弦所对的弧
C.圆是中心对称图形,圆心是它的对称中心
D.圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
【分析】根据将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合,显然说明了圆的轴对称性.
【解答】解:将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合,由此说明圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
故选:D.
【点评】考查了轴对称图形的概念,圆的对称轴为直径所在的直线或过圆心的直线.
2.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是( )
A.40° B.50° C.60° D.80°
【分析】利用等边对等角即可证得∠C=∠DOC=20°,然后根据三角形的外角等于不相邻的两个内角的和即可求解.
【解答】解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故选:C.
【点评】本题主要考查了三角形的外角的性质和等腰三角形的性质,正确理解圆的半径都相等是解题的关键.
3.如图,⊙O中点A、O、D以及点E、D、C分别在同一直线上,图中弦的条数为( )
A.2 B.3 C.4 D.5
【分析】根据弦的定义可以判断图中有几条弦,从而可以解答本题.
【解答】解:由图可知,
在圆中,线段AB,线段EC是弦,线段BC是弦,
故选:B.
【点评】本题考查圆的认识,解题的关键是明确弦的定义,注意直径是圆内最长的弦.
4.在平面直角坐标系中,⊙C的圆心坐标为(1,0),半径为1,AB为⊙C的直径,若点A的坐标为(a,b),则点B的坐标为( )
A.(﹣a﹣1,﹣b) B.(﹣a+1,﹣b) C.(﹣a+2,﹣b) D.(﹣a﹣2,﹣b)
【分析】作AD⊥x轴于D,BE⊥x轴于E,易证得Rt△ACD≌Rt△BCE,则AD=BE,DC=CE,由于点A的坐标为(a,b),⊙C的圆心坐标为(1,0),BE=AD=b,EC=CD=a﹣1,OE=1﹣(a﹣1)=﹣a+2,根据坐标的表示方法即可得到B点坐标为(﹣a+2,﹣b),同样得到当点A圆上的任何位置都有此结论.
【解答】解:如图,作AD⊥x轴于D,BE⊥x轴于E,
∵AB为⊙C的直径,
∴CA=CB,
而∠ACD=∠BCE,
∴Rt△ACD≌Rt△BCE,
∴AD=BE,DC=CE,
∵点A的坐标为(a,b),⊙C的圆心坐标为(1,0),
∴BE=AD=b,EC=CD=a﹣1,
∴OE=1﹣(a﹣1)=﹣a+2,
∴B点坐标为(﹣a+2,﹣b),
当点A圆上的任何位置都有此结论.
故选:C.
【点评】本题考查了圆的认识:过圆心的弦叫圆的直径.也考查了坐标的表示以及三角形全等的判定与性质.
5.已知⊙O的直径AB=6cm,则圆上任意一点到圆心的距离等于( )
A.2 cm B.2.5 cm C.3 cm D.无法确定
【分析】根据⊙O的直径AB=6cm,利用圆的性质得出圆上各点到圆心的距离等于半径进而得出答案.
【解答】解:∵⊙O的直径AB=6cm,故圆的半径为3cm,
∴圆上任意一点到圆心的距离等于3cm,
故选:C.
【点评】此题主要考查了圆的性质,根据圆上各点到圆心的距离等于半径是解题关键.
初中数学25.3 用频率估计概率一课一练: 这是一份初中数学25.3 用频率估计概率一课一练,文件包含253用频率估计概率练习学生版docx、253用频率估计概率练习教师版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
人教版九年级上册25.1 随机事件与概率综合与测试课后复习题: 这是一份人教版九年级上册25.1 随机事件与概率综合与测试课后复习题,文件包含251随机事件与概率练习学生版docx、251随机事件与概率练习教师版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
人教版九年级上册第二十四章 圆24.3 正多边形和圆当堂达标检测题: 这是一份人教版九年级上册第二十四章 圆24.3 正多边形和圆当堂达标检测题,文件包含243正多边形与圆练习学生版docx、243正多边形与圆练习教师版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。













