2021年陕西省西安市灞桥区中考数学模拟试卷（word版 含答案）

这是一份2021年陕西省西安市灞桥区中考数学模拟试卷（word版 含答案），共26页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2021年陕西省西安市灞桥区中考数学模拟试卷
学校:___________姓名：___________班级：___________考号：___________


一、单选题
1．计算：（　　　）
A．1 B．0 C．2020 D．﹣2020
2．如图，几何体的左视图是( )

A． B．
C． D．
3．如果∠A和∠B的两边分别平行，那么∠A和∠B的关系是( )
A．相等 B．互余或互补 C．互补 D．相等或互补
4．已知正比例函数y＝3x，若该正比例函数图象经过点（a，4a﹣1），则a的值为（　　）
A．1 B．﹣1 C． D．﹣
5．下列运算结果正确的是（ ）
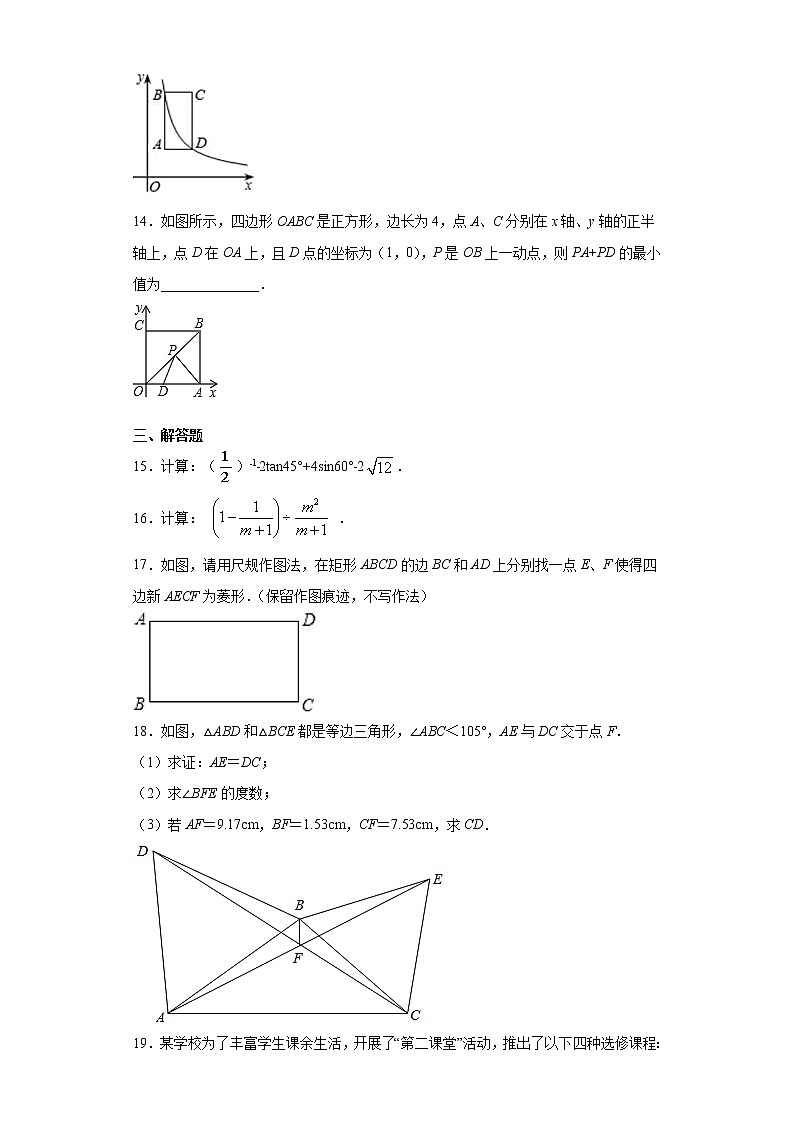
A．（a2）3＝a5 B．（a﹣b）2＝a2﹣b2
C．﹣3a2b﹣2a2b＝﹣a2b D．﹣a2b÷a2＝﹣b
6．在平面直角坐标系中，将一次函数的图象沿x轴向左平移m（m≥0）个单位后经过原点O，则m的值为（　　）
A． B． C．2 D．
7．如图，在矩形ABCD中，AB＝10，P是CD边上一点，M、N、E分别是PA、PB、AB的中点，以下四种情况，哪一种四边形PMEN不可能为矩形（ ）

A．AD＝3 B．AD＝4 C．AD＝5 D．AD＝6
8．如图，AB为⊙O的直径，C，D为⊙O上的点，＝．若∠CBA＝40°，则∠CBD的大小为（ ）

A．50° B．40° C．25° D．20°
9．将抛物线y＝x2向左平移4个单位后，再向下平移2个单位，则所得到的抛物线的解析式为（ ）
A．y＝（x+4）2+2 B．y＝（x+4）2﹣2 C．y＝（x﹣4）2+2 D．y＝（x﹣4）2﹣2
10．如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，BE是AC边的中线，CF是∠ACB的角平分线，CF交AD于点G，交BE于点H，下面说法正确的是（ ）
①△ABE的面积＝△BCE的面积；②∠FAG＝∠FCB；③AF＝AG；④BH＝CH．

A．①②③④ B．①②③ C．②④ D．①③

二、填空题
11．写出一个比大的无理数：____________．
12．一个多边形的每一个外角都等于30°，则这个多边形的边数是__．
13．如图，矩形ABCD的边AB与y轴平行，顶点A的坐标为（1，m），C（3，m+6），那么图象同时经过点B与点D的反比例函数表达式为____．

14．如图所示，四边形OABC是正方形，边长为4，点A、C分别在x轴、y轴的正半轴上，点D在OA上，且D点的坐标为（1，0），P是OB上一动点，则PA+PD的最小值为______________．


三、解答题
15．计算：（）﹣1﹣2tan45°+4sin60°﹣2．
16．计算： ．
17．如图，请用尺规作图法，在矩形ABCD的边BC和AD上分别找一点E、F使得四边新AECF为菱形．（保留作图痕迹，不写作法）

18．如图，△ABD和△BCE都是等边三角形，∠ABC＜105°，AE与DC交于点F．
（1）求证：AE＝DC；
（2）求∠BFE的度数；
（3）若AF＝9.17cm，BF＝1.53cm，CF＝7.53cm，求CD．

19．某学校为了丰富学生课余生活，开展了“第二课堂”活动，推出了以下四种选修课程：．绘画；．唱歌；．跳舞；．演讲；．书法．学校规定：每个学生都必须报名且只能选择其中的一个课程．学校随机抽查了部分学生，对他们选择的课程情况进行了统计，并绘制了如下两幅不完整的统计图．

请结合统计图中的信息解决下列问题：
（1）这次抽查的学生人数是多少人？
（2）将条形统计图补充完整．
（3）求扇形统计图中课程所对应扇形的圆心角的度数．
（4）如果该校共有1200名学生，请你估计该校选择课程的学生约有多少人．
20．如图，小华和同伴在游玩期间，发现在某地小山坡的点处有颗梅花树，他想利用平面镜测量的方式计算一下梅花树到山脚下的距离，即的长度，小华站在点的位置，让同伴移动平面镜至点处，此时小华在平面镜内可以看到点，且米，米，，已知小华的身高为米，请你利用以上的数据求出的长度．（结果保留根号）

21．甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系；折线表示轿车离甲地的距离y（千米）与时间x（时）之间的函数关系，请根据图象解答下列问题．
（1）轿车到达乙地时，求货车与甲地的距离．
（2）求线段对应的函数表达式．
（3）在轿车行进过程中，轿车行驶多少时间，两车相距15千米．

22．小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯，已知两个陌生人到1至3层的任意一层出电梯，并设甲在层出电梯，乙在b层出电梯．
（1）请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率．
（2）小亮和小芳打赌说：“若甲、乙在同一层或相邻楼层出电梯，则小亮胜，否则小芳胜”．该游戏是否公平？并说明理由．
3层
2层
1层
车库

23．如图，直线AM与⊙O相切于点A，弦BCAM，连接BO并延长，交⊙O于点E，交AM于点F，连接CE并延长，交AM于点D．
（1）求证：CEOA；
（2）若⊙O的半径R＝13，BC＝24，求AF的长．

24．如图，抛物线y＝﹣x2+bx+c过等腰Rt△OAB的A，B两点，点B在点A的右侧，直角顶点A（0，3）．
（1）求抛物线的表达式．
（2）P是AB上方抛物线上的一点，作PQ⊥AB交OB于点Q，连接AP，是否存在点P，使四边形APQO是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．

25．如图1，四边形ABCD是矩形，点P是对角线AC上的一个动点（不与A、C重合），过点P作PE⊥CD于点E，连接PB，已知AD＝3，AB＝4，设AP＝m．
（1）当m＝1时，求PE的长；
（2）连接BE，试问点P在运动的过程中，能否使得△PAB≌△PEB？请说明理由；
（3）如图2，过点P作PF⊥PB交CD边于点F，设CF＝n，试判断5m+4n的值是否发生变化，若不变，请求出它的值；若变化，请说明理由．



参考答案
1．A
【分析】
根据零指数幂的运算法则计算即可．
【详解】
(﹣2020)0=1．
故选：A．
【点睛】
本题考查了零指数幂，正确掌握零指数幂的运算法则是解题的关键．
2．A
【分析】
根据从左边看得到的图形是左视图，可得答案．
【详解】
解：如图所示，其左视图为：
．
故选A．
【点睛】
本题考查了简单组合体的三视图，从左边看得到的图形是左视图，注意看不到而且是存在的线是虚线．
3．D
【详解】
解：如图知∠A和∠B的关系是相等或互补．
故选D.

4．A
【分析】
把点的坐标代入函数的解析式，即可得出关于a的方程，求出方程的解即可．
【详解】
解：∵正比例函数y=3x的图象经过点（a，4a-1），
∴代入得：4a-1=3a，
解得：a=1，
故选：A．
【点睛】
本题考查了一次函数图象上点的坐标特征和解一元一次方程，能得出关于a的一元一次方程是解此题的关键．
5．D
【分析】
根据各个选项中的式子，可以计算出正确的结果，从而可以解答本题．
【详解】
解：（a2）3＝a6，故选项A不符合题意；
（a﹣b）2＝a2﹣2ab+b2，故选项B不符合题意；
﹣3a2b﹣2a2b＝﹣5a2b，故选项C不符合题意；
﹣a2b÷a2＝﹣b，故选项D符合题意；
故选：D．
【点睛】
本题考查整式的混合运算，解答本题的关键是明确整式混合运算的计算方法．
6．D
【分析】
先求出平移后的解析式，然后把原点坐标代入即可求出m的值．
【详解】
解：将一次函数的图象沿x轴向左平移m个单位后得：
，
把(0，0)代入，得，
解得m=．
故选D．
【点睛】
本题考查的是一次函数图象的平移，熟练掌握“左加右减，上加下减”是解答本题的关键．
7．D
【分析】
先证四边形PMEN是平行四边形，当∠APB=90°时，四边形PMEN是矩形，设DP=x，CP=10-x，再由勾股定理得出方程，分别计算即可．
【详解】
解：∵四边形ABCD是矩形，
∴AD＝BC，AB＝CD＝10，∠C＝∠D＝90°，
∵M、N、E分别是PA、PB、AB的中点，
∴ME、NE是△ABP的中位线，
∴ME∥BP，NE∥AP，
∴四边形PMEN是平行四边形，
当∠APB＝90°时，四边形PMEN是矩形，
设DP＝x，CP＝10﹣x，
由勾股定理得：AP2＝AD2+x2，BP2＝BC2+（10﹣x）2，AP2+BP2＝AB2，
∴AD2+x2+AD2+（10﹣x）2＝102，
AD2+x2﹣10x＝0，
①当AD＝3时，x2﹣10x+9＝0，
x＝1或x＝9，符合题意；
②当AD＝4时，x2﹣10x+16＝0，
x＝2或x＝8，符合题意；
③当AD＝5时，x2﹣10x+25＝0，
x＝5，符合题意；
④当AD＝6时，x2﹣10x+36＝0，无解；
故选：D．
【点睛】
本题考查了矩形的判定与性质、平行四边形的判定与性质以及勾股定理等知识；熟练掌握矩形的性质和勾股定理是解题的关键．
8．C
【分析】
连接AC、AD，如图，根据圆周角定理得到∠ACB＝90°，利用互余计算出∠BAC＝50°，然后利用圆周角定理得到∠CAD＝∠BAD＝∠CBD∠BAC．
【详解】
解：连接AC、AD，如图，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠BAC＝90°﹣∠CBA＝90°﹣40°＝50°，
∵＝，
∴∠CAD＝∠BAD＝∠CBD＝∠BAC＝×50°＝25°．
故选：C．

【点睛】
本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
9．B
【分析】
根据“左加右减、上加下减”的原则进行解答即可．
【详解】
解：将抛物线y＝x2向左平移4个单位所得抛物线解析式为：y＝（x+4）2；
再向下平移2个单位后抛物线解析式为：y＝（x+4）2﹣2．
故选：B．
【点睛】
本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
10．D
【分析】
根据三角形的面积公式进行判断①，根据三角形的内角和定理求出∠FAG＝∠ACB，再判断②即可，根据三角形的内角和定理求出∠AFG＝∠AGF，再根据等腰三角形的判定判断③即可，根据等腰三角形的判定判断④即可．
【详解】
解：∵BE是AC边的中线，
∴AE＝CE，
∵△ABE的面积＝，△BCE的面积＝AB，
∴△ABE的面积＝△BCE的面积，故①正确；
∵AD是BC边上的高，
∴∠ADC＝90°，
∵∠BAC＝90°，
∴∠DAC+∠ACB＝90°，∠FAG+∠DAC＝90°，
∴∠FAG＝∠ACB，
∵CF是∠ACB的角平分线，
∴∠ACF＝∠FCB，∠ACB＝2∠FCB，
∴∠FAG＝2∠FCB，故②错误；
∵在△ACF和△DGC中，∠BAC＝∠ADC＝90°，∠ACF＝∠FCB，
∴∠AFG＝180°﹣∠BAC﹣∠ACF，∠AGF＝∠DGC＝180°﹣∠ADC﹣∠FCB，
∴∠AFG＝∠AGF，
∴AF＝AG，故③正确；
根据已知不能推出∠HBC＝∠HCB，即不能推出HB＝HC，故④错误；
即正确的为①③，
故选：D．
【点睛】
本题考查了角平分线的定义，三角形的面积，三角形的中线，三角形的高，三角形内角和定理等知识点，能综合运用定理进行推理是解此题的关键．
11．答案不唯一，如：
【分析】
无理数是指无限不循环小数，根据定义和实数的大小比较法则写出一个即可．
【详解】
一个比4大的无理数如．
故答案为．
【点睛】
本题考查了估算无理数的大小，实数的大小比较的应用，能估算无理数的大小是解此题的关键，此题是一道开放型的题目，答案不唯一．
12．12
【分析】
多边形的外角和为360°，而多边形的每一个外角都等于30°，由此做除法得出多边形的边数．
【详解】
∵360°÷30°=12，
∴这个多边形为十二边形，
故答案为：12．
【点睛】
本题考查了多边形的内角与外角．关键是明确多边形的外角和为360°．
13．
【分析】
设反比例函数的解析式为（k≠0），根据矩形的性质及A、C坐标可得B（1，m+6），D（3，m），根据点B、D在反比例函数图象上，代入可得关于m的方程，即可求出m的值，进而可求出k值，可得答案．
【详解】
设反比例函数的解析式为（k≠0），
∵四边形ABCD是矩形，A（1，m），C（3，m+6），
∴B（1，m+6），D（3，m），
∵点B、D在反比例函数图象上，
∴k=m+6=3m，
解得：m=3，
∴k=3m=9，
∴反比例函数解析式为，
故答案为：
【点睛】
本题考查矩形的性质及待定系数法求反比例函数解析式，正确表示出点B、D的坐标是解题关键．
14．
【分析】
作出点D关于OB的对称点D′，则D′的坐标是（0，1）．则PD+PA的最小值就是AD′的长，利用勾股定理即可求解．
【详解】
解：作出点D关于OB的对称点D′，
则D′的坐标是（0，1）．
则PD+PA的最小值就是AD′的长．
则OD′＝1，
因而AD′＝＝．
则PD+PA和的最小值是．
故答案为：．

【点睛】
本题考查了正方形的性质，以及最短路线问题，正确作出P的位置是关键．
15．
【分析】
直接利用负指数幂的性质、特殊角的三角函数值、二次根式的性质化简得出答案．
【详解】
解：原式＝2﹣2×1+4×﹣2×
＝2﹣2+﹣
＝﹣．
【点睛】
本题主要考查实数的运算，解题的关键是熟知负指数幂的性质、特殊角的三角函数值、二次根式的性质．
16．
【分析】
首先把分式通分，把除法转化成乘法，然后进行约分即可．
【详解】
解：原式
．
【点睛】
本题主要考查分式的混合运算，通分、约分是解答的关键．
17．见解析
【分析】
连接AC，作线段AC的垂直平分线分别交BC于点E，AD于点F，则四边形AECF即为所作菱形．
【详解】
解：如图，四边形AECF为所作．

【点睛】
本题考查作图-作垂直平分线．掌握线段的垂直平分线的性质和菱形的性质是解答本题的关键．
18．（1）见解析；（2）60°；（3）18.23cm
【分析】
（1）由等边三角形的性质可知∠DBA＝∠EBC＝60°，BD＝AB，BC＝BE．从而可证∠DBC＝∠ABE．即可利用“SAS”可证明△DBC≌△ABE，得出结论AE＝DC．
（2）过点B作BN⊥CD于N，BH⊥AE于H．由△DBC≌△ABE可知∠BEH＝∠BCN，∠BDF＝∠BAF．再结合等边三角形的性质可求出∠FDA+∠DAF＝120°，进而求出∠DFA＝180°-120°＝60°，即求出∠DFE＝180°-60°＝120°．即可利用“AAS”证明△BEH≌△BCN，得出结论BH＝BN，即得出BF平分∠DFE，即可求出∠BFE＝60°．
（3）延长BF至Q，使FQ＝AF，连接AQ．根据所作辅助线可知∠AFQ＝∠BFE＝60°，即证明△AFQ是等边三角形，得出结论AF＝AQ＝BQ，∠FAQ＝60°．又可证明∠DAF＝∠BAQ．利用“SAS”可证明△DAF≌△BAQ，即得出DF＝BQ＝BF+FQ＝BF+AF，最后即可求出CD＝DF+CF＝BF+AF+CF＝1.53+9.17+7.53＝18.23cm．
【详解】
（1）证明：∵△ABD和△BCE都是等边三角形，
∴∠DBA＝∠EBC＝60°，BD＝AB，BC＝BE，
∴∠DBA+∠ABC＝∠EBC+∠ABC，即∠DBC＝∠ABE，
∵在△DBC和△ABE中，，
∴△DBC≌△ABE（SAS），
∴AE＝DC；
（2）解：如图，过点B作BN⊥CD于N，BH⊥AE于H．

∵△DBC≌△ABE，
∴∠BEH＝∠BCN，∠BDF＝∠BAF，
∵△ABD是等边三角形，
∴∠BDA+∠BAD＝120°，
∴∠FDA+∠DAF＝120°，
∴∠DFA＝180°-120°＝60°，
∴∠DFE＝180°-60°＝120°，
在△BEH和△BCN中，
，
∴△BEH≌△BCN（AAS），
∴BH＝BN，
∴BF平分∠DFE，
∴∠BFE＝∠DFE＝×120°＝60°；
（3）解：如图，延长BF至Q，使FQ＝AF，连接AQ．
则∠AFQ＝∠BFE＝60°，
∴△AFQ是等边三角形，
∴AF＝AQ＝BQ，∠FAQ＝60°，
∵△ABD是等边三角形，
∴AD＝AB，∠DAB＝60°，
∴∠DAB+∠BAF＝∠BAF+∠FAQ，即∠DAF＝∠BAQ，
在△DAF和△BAQ中，，
∴△DAF≌△BAQ（SAS），
∴DF＝BQ＝BF+FQ＝BF+AF，
∴CD＝DF+CF＝BF+AF+CF＝1.53+9.17+7.53＝18.23cm．

【点睛】
本题为三角形综合题．考查等边三角形的判定和性质，全等三角形的判定和性质，三角形内角和定理以及角平分线的判定和性质．正确的作出辅助线也是解答本题的关键．
19．（1）100人；（2）20人，详见解析；（3）；（4）约有300人
【分析】
（1）由D课程的人数及其所占百分比可得总人数；
（2）根据各课程人数之和等于总人数求出C课程的人数，从而补全图形；
（3）用360°乘以课程E人数所占比例即可得；
（4）用总人数乘以样本中课程D人数所占比例即可得．
【详解】
解：（1）这次调查的学生人数是（人）．
（2）（人），补全条形统计图如图所示．

（3）课程所对应扇形的圆心角的度数是．
（4）（人），
估计该校1200名学生中报课程的学生约有300人．
【点睛】
本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
20．米
【分析】
过作于点，设DF=x，根据∠CDE=120°求出∠EDF=60°，进而将DE、EF分别用x的代数式表示，最后根据△ABC∽△EFC线段成比例求出x的值即可求解．
【详解】
解：如图所示，过作于点，

，
设为米，米，米，
，，
，，代入数据：
即，解得，
则，
的长度为米．
【点睛】
本题考查相似三角形测高，相似三角形的应用，本题的关键是能证明△ABC∽△EFC，进而通过边成比例求解．
21．（1）；（2）；（3）或．
【分析】
（1）根据图象可知货车5小时行驶300千米，由此计算其速度，再根据图象得到货车出发4.5小时，轿车到达乙地，由此计算此时货车的路程，继而解题；
（2）设段函数解析式为，将C、D两点坐标代入解析式，用待定系数法解题；
（3）当时，分两种情况讨论①货车在轿车前15千米时，②轿车在货车前15千米时，分别列出相应的一元一次方程，解方程即可．
【详解】
（1）由图可知货车的速度．
∵轿车到达乙地的时间为货车出发后．
∴当轿车到达乙地时，货车行驶路程为：．
答：轿车到达乙地后，货车与甲地相距．
（2）设段函数解析式为，
在上，
，
解得，
段函数解析式为．
（3）线段表示的解析式为，
设段解析式为，
∵过，
∴，
解得，
段解析式为．
当时，两车相距15千米，
则，
解得，
，
故不符合题意，故舍弃；
当时，
①货车在轿车前15千米时，
则，
解得；
②轿车在货车前15千米时，
则，
解得．
答：当轿车行时或两车相距15千米．
【点睛】
本题考查函数图象、一次函数的实际应用、一次函数的解析式等知识，其中涉及待定系数法、分类讨论法等，是重要考点，难度较易，掌握相关知识是解题关键．
22．（1）；（2）不公平，证明见解析．
【分析】
（1）画树状图得出所有的等可能的结果数，找出两人在同一层出电梯的结果数，利用概率公式计算概率即可；
（2）分别求出两人获胜的概率，比较大小即可得出结论．
【详解】
解析 （1）由题可得树状图如下图所示：

由图可知，一共有9种等可能的结果，其中两人在同一楼层出现的有3种结果，则两人在同一楼层出现的概率；
（2）两人在相邻楼层出电梯的概率，
∴小亮获胜的概率为，
∴小芳获胜的概率为，
，
∴该游戏不公平．
【点睛】
本题考查画树状图或列表法求概率、游戏的公平性，会画树状图或列表法求概率，会根据概率的大小判断游戏的公平性是解答的关键．
23．（1）见解析；（2）
【分析】
（1）根据平行线的性质和切线的性质定理即可得到结论；
（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．
【详解】
（1）证明：如图

∵BE是⊙O的直径，
∴CE⊥BC，
∵BC∥AM，
∴CD⊥AM，
∵AM是⊙O的切线，
∴OA⊥AM，
∴CE∥OA；
（2）解：∵⊙O的半径R＝13，
∴OA＝13，BE＝26，
∵BC＝24，
∴CE＝＝10，
∵BC∥AM，
∴∠B＝∠AFO，
∵∠C＝∠A＝90°，
∴△BCE∽△FAO，
∴，
∴
∴AF＝．
【点睛】
本题考查了切线的性质，相似三角形的判定和性质，勾股定理，平行线的性质，圆周角定理，正确的识别图形是解题的关键．
24．（1）y＝﹣x2+3x+3；（2）存在，当P（2，5）时，四边形APQO是平行四边形．
【分析】
（1）根据题意得到点B的坐标，把A，B的坐标代入二次函数解析式，列出关于系数b、c的方程组，通过解方程组可以求得它们的值；
（2）由条件可知OA∥PQ，则PQ＝3时，OAPQ为平行四边形，设P（m，﹣m2+3m+3），Q（m，m），可得关于m的方程，求出m的值即可求解．
【详解】
解：（1）∵A（0，3），等腰Rt△OAB，
∴AB＝3＝OA，
∴B（3，3），
将点A、B的坐标代入y＝﹣x2+bx+c得：
∴，
∴抛物线的表达式为y＝﹣x2+3x+3；
（2）存在，
∵B（3，3），
∴OB的解析式为y＝x，
∵y＝﹣x2+3x+3，
设P（m，﹣m2+3m+3），Q（m，m），
∵PQ⊥AB，OA⊥AB，
∴OA∥PQ，
若四边形APQO是平行四边形，
∴PQ＝﹣m2+3m+3﹣m＝3，
解得m＝0（舍去），m＝2，
当m＝2时，y＝﹣4+6+3＝5，
∴p（2，5），
即当P（2，5）时，四边形APQO是平行四边形．
【点睛】
此题是二次函数综合题，考查了待定系数法求二次函数的解析式、平行四边形的判定与性质．熟练掌握方程的思想方法是解题的关键．
25．（1）PE＝；（2）不能，理由见解析；（3）不变，5m+4n＝16．
【分析】
（1）根据勾股定理得出AC，进而利用相似三角形的判定和性质解答即可；
（2）根据全等三角形的性质和勾股定理解答即可；
（3）根据相似三角形的判定和性质以及勾股定理解答即可．
【详解】
解：（1）连接BE，
由已知：在Rt△ADC中，AC＝，
当AP＝m＝1时，PC＝AC﹣AP＝5﹣1＝4，
∵PE⊥CD，
∴∠PEC＝∠ADC＝90°，
∵∠ACD＝∠PCE，
∴△ACD∽△PCE，
∴，
即，
∴PE＝；
（2）如图1，当△PAB≌△PEB时，

∴PA＝PE，
∵AP＝m，则PC＝5﹣m，
由（1）得：△ACD∽△PCE，
∴，
∴PE＝，
由PA＝PE，即，
解得：m＝，
∴EC＝，
∴BE＝，
∴△PAB与△PEB不全等，
∴不能使得△PAB≌△PEB；
（3）如图2，延长EP交AB于G，

∵BP⊥PF，
∴∠BPF＝90°，
∴∠EPF+∠BPG＝90°，
∵EG⊥AB，
∴∠PGB＝90°，
∴∠BPG+∠PBG＝90°，
∴∠PBG＝∠EPF，
∵∠PEF＝∠PGB＝90°，
∴△BPG∽△PFE，
∴，
由（1）得：△PCE∽△ACD，PE＝，
∴，
即，
∴EC＝，
∴BG＝EC＝，
∴，
∴5m+4n＝16．
【点睛】
此题考查四边形的综合题，关键是根据相似三角形的判定和性质以及勾股定理进行解答．