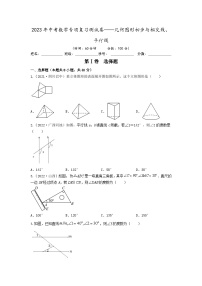
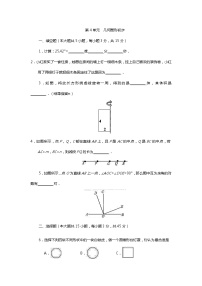
初中数学人教版七年级上册第四章 几何图形初步综合与测试练习

这是一份初中数学人教版七年级上册第四章 几何图形初步综合与测试练习，共16页。试卷主要包含了请将答案正确填写在答题卡上，下列命题①同位角相等，如图，∠AOB的角平分线是，如图，是的平分线，，，则等于，下列说法正确的是，如果与是同旁内角，且，则，下列说法正确的个数为等内容，欢迎下载使用。
保密★启用前几何图形初步认识专项试卷试卷副标题考试范围：xxx；考试时间：100分钟；命题人：xxx注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上 第I卷（选择题）请点击修改第I卷的文字说明 一、单选题1．如图，a∥b，∠1=115°，∠2=95°，则∠3为（  ）A．120° B．135° C．150° D．145°2．小张同学的座右铭是“态度决定一切”，他将这几个字写在一个正方体纸盒的每个面上，其平面展开图如图所示，那么在该正方体中，和“一”相对的字是（ ）A．态 B．度 C．决 D．切3．如图，∠AOB=70°，射线OC是可绕点O旋转的射线，当∠BOC=15°时，则∠AOC的度数是（   ）A．55° B．85° C．55°或85° D．不能确定4．下列命题①同位角相等．②经过一点有且只有一条直线平行于已知直线．③从直线外一点到这条直线的垂线段，叫做点到直线的距离．④互为邻补角的两个角的平分线互相垂直．其中真命题有（     ）A．1个 B．2个 C．3个 D．4个5．如图，∠AOB的角平分线是（   ）A．射线OB B．射线OE C．射线OD D．射线OC6．如图，是的平分线，，，则等于（ ）A．75° B．70° C．65° D．60°7．如图AB∥CD，AE平分∠CAB且交CD于点D，若∠EAB＝30°，则∠C的度数为（   ）A．30° B．60° C．120° D．150°8．下列说法正确的是（    ）A．若AB＝BC,则点B为线段AC的中点 B．射线AB和射线BA是同一条射线C．两点之间的线段就是两点之间的距离 D．两点确定一条直线9．如果与是同旁内角，且，则A、为   B、为  C、为或  D、大小不定10．下列说法正确的个数为（   ）  ①柱体的上、下两个面一样大；②圆柱的侧面展开图是长方形；③正方体有6个顶点；④圆锥有2个面，且都是曲面；⑤球仅由1个面围成，这个面是平面；⑥三棱柱有5个面，且都是平面（     ）A．1    B．2    C．3    D．411．如图表示的是由5个小立方块搭建而成的几何体，从上面看所得到的图形是（   ）A． B．C． D． 第II卷（非选择题）请点击修改第II卷的文字说明 二、填空题12．如图，将含有30°角的三角板的直角顶点放在直尺的一边上，若，则的度数是__________．13．已知∠α=73°，则∠α的余角是____________，∠α的补角是________________．14．某正方体的平面展开图如图所示，与其对面的数字互为相反数，则的值为__________．15．已知线段AB＝16 cm，直线AB上有一点C，且BC＝10 cm，M是线段AC的中点，则AM的长为________ cm. 三、解答题16．按语句画图：任取一点O，以O为端点画射线OA和OB，使∠AOB＝40°；分别在OA和OB上截取OC和OD，使OC＝OD＝3 cm，画出OC和OD的中点M，N，连接CD和MN.(1)测量∠OCD，∠OMN，∠ODC，∠ONM的度数；(2)你发现什么规律了吗？试着表述一下．17．如图，点在线段上，，，点、分别是、的中点．（1）求线段的长度．（2）若为线段上任意一点且满足其他条件不变，你能猜想的长度吗？请你用一句简洁的话描述你发现的结论．（3）若为线段的延长线上，且满足，、分别为、的中点，你能猜想出的长度吗？请画出图形并写出你的结论．18．观察下列多面体，把下表补充完整，并回答问题.（1）根据上表中的规律推断，十四棱柱共有___个面，共有___个顶点，共有____条棱.（2）若某个棱柱由30个面构成，则这个棱柱为____棱柱.（3）若一个棱柱的底面多边形的边数为n，则它有____个侧面，共有___个面，共有____个顶点，共有_____条棱.（4）观察表中的结果，你能发现a，b，c之间有什么关系吗？请写出关系式．19．如图所示，有两根木条AB和CD，其中AB的长为90，CD的长为140，在它们的中点处各有一个小圆孔M和N（圆孔直径忽略不计，M，N抽象成两个点），将它们的一端重合，放置在同一条直线上，求此时两根木条的小圆孔之间的距离.20．读下列语句，并画出图形：直线AB、CD是相交直线，点P是直线AB，CD外一点，直线EF经过点P，且与直线AB平行，与直线CD相交于点E．21．如图，点B是线段AC上一点，且AB＝24cm，BC＝AB，（1）试求出线段AC的长；（2）如果点O是线段AC的中点，请求线段OB的长．22．如图所示，一个圆柱体，一只蚂蚁在下底面的点A处，想爬到上底面的点B处，请你设计最短的路线，在图上表示出来，并说明原因．
参考答案1．C.【解析】试题分析：如图，过∠2的顶点作n∥a，根据两直线平行，同旁内角互补可得∠4=180°﹣∠1=180°﹣115°=65°，，又因∠5=∠2﹣∠4=95°﹣65°=30°，根据平行于同一条直线的两条直线平行可得n∥b，再由两直线平行，同旁内角互补可得∠3=180°﹣∠5=180°﹣30°=150°．故答案选C.考点：平行线的性质．2．A【解析】试题分析：正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，据此可得和“一”相对的字．试题解析：正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，所以和“一”相对的字是： 态．故选A．考点：几何体的展开图．3．C【解析】试题解析：当OC在∠AOB的内部时，∠AOC=∠AOB-∠BOC=70°-15°=55°；当OC在∠AOB的外部时，∠AOC=∠AOB+∠BOC=70°+15°=85°，所以∠AOC的度数为55°或85°．故选C．点睛：会进行角度的和、差、倍、分的计算以及度、分、秒的换算．4．A【分析】根据正确的命题是真命题，错误的命题是假命题可得答案．【详解】两直线平行，同位角相等，所以①为假命题；经过直线外一点，有且只有一条直线与这条直线平行，所以②为假命题；从直线外一点到这条直线的垂线段的长，叫做这点到直线的距离，所以③为假命题；互为邻补角的两个角的角平分线互相垂直是正确的，所以④为真命题；故选：A．【点睛】本题主要考查了命题与定理，关键是掌握真命题与假命题的定义．判断命题的真假关键是要熟悉课本中的性质定理．5．B【分析】借助于图中的量角器得到各个角的度数，再结合角平分线的定义进行分析判断即可.【详解】由图中信息可知，∠AOB=70°，∠AOE=∠BOE=35°，∴∠AOB的平分线是射线OE.故选B.【点睛】“能用量角器测量角的度数，且熟悉角平分线的定义”是解答本题的关键.6．D【分析】设∠BOD为x°，，得出∠BOC＝2x°，利用角平分线的性质得出∠AOB＝2∠BOC，根据可以求出x°,再求出．【详解】解：设∠BOD为x°，则∠COD为3x°，∴∠COB＝∠COD﹣∠BOD＝2x°，∵OC是∠AOB的平分线，∴∠AOB＝2∠COB＝4x°，∵∠AOD＝75°，∴∠AOD=∠BOD+∠AOB＝5 x°＝75°∴x=15∴∠AOB＝4×15°＝60°．故选：D．【点睛】此题主要考查了角的计算和角平分线的定义，能够正确得出∠BOC＝2∠BOD是解题的关键．7．C【分析】根据角平分线的定义可得∠CAB的度数，再根据平行线的性质解答即可．【详解】解：∵AE平分∠CAB，∠EAB＝30°，∴∠CAB=2∠EAB＝60°，∵AB∥CD，∴∠C+∠CAB＝180°，∴∠C=180°－∠CAB =120°．故选：C．【点睛】本题考查了角平分线的定义和平行线的性质，属于基本题型，熟练掌握平行线的性质是关键．8．D【分析】利用直线的定义、射线的定义、以及线段的性质和两点之间距离意义，分别分析得出答案.【详解】A．错误，A，B，C不一定在一条直线上.B．错误，射线是有方向的.C．错误，连接两点的线段长度叫做两点间的距离.D．正确.【点睛】此题主要考查直线、射线、线段的定义，准确理解它们的相同点和不同点是解题的关键.9．D【解析】试题分析：同旁内角，即两个角位于同一侧，但是大小不知考点：同旁内角定义点评：若是同旁内角是位于两条平行线之间，则此时符合“两直线平行，同旁内角互补”，即10．C【解析】【详解】试题解析：①正确，②正确，③错误，正方体有8个顶点，④错误，有一个是曲面，有一个是平面, ⑤错误，球仅由1个面围成，这个面是曲面；⑥正确.故选C.11．C【分析】从上面看得到从左往右3列，正方形的个数依次为1，1，2，依此判别出图形即可．【详解】从上面看有三列，第一列是1个正方体，中间一列是1个正方体，第三列是2个正方体，故选：C．【点睛】本题主要考查了简单几何体的三视图，关键是掌握三视图的定义，从上面看它得到的平面图形是俯视图．12．【分析】根据平行线的性质得，，根据对顶角相等可得，再根据三角板的性质、三角形外角的性质得，，代入求解即可．【详解】如图∵，∴，∴∵，∴故答案为：．【点睛】本题考查了三角板跟直尺的角度问题，掌握平行线的性质、对顶角的性质、三角板的性质、三角形外角的性质是解题的关键．13．17°    107°    【解析】∠α的余角=90°-73°=17°，∠α的补角=180°-73°=107°．故答案为17°，107°．14．-2【分析】利用正方体及其表面展开图的特点可知，a与2所在的面为相对面，再根据“与其对面的数字互为相反数”即可得出的值．【详解】解：这是一个正方体的平面展开图，共有六个面，其中面与2所在的面相对．
∵与其对面的数字互为相反数，
∴a=-2．
故答案为：-2．【点睛】本题考查正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．也考查了相反数的概念．15．3或13【分析】本题没有给出图形，在画图时，应考虑到A、B、C三点之间的位置关系的多种可能，再根据正确画出的图形解题．同时利用中点性质转化线段之间的倍分关系【详解】当点C在AB中间时，如图，AC=AB-BC=16-10=6，AM=AC=3cm，当点C在AB的外部时，AC=AB+BC=16+10=26，AM=AC=13．故答案为3或13．【点睛】在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性．在今后解决类似的问题时，要防止漏解．16．（1）四个角的度数都相等，均为70°.（2）顶角相等(同)的等腰三角形的底角也相等．【解析】分析：通过作图可得△OMN和△OCD均为等腰三角形，通过测量可得∠OCD，∠OMN，∠ODC，∠ONM的度数，进而得出规律.详解：如图．(1)四个角的度数都相等，均为70°.(2)顶角相等(同)的等腰三角形的底角也相等．点睛：本题考查通过作图、测量得出等腰三角形的性质.17．（1）；（2）在线段上时，长度为的一半；（3），画出图形见解析；在线段所在直线上时就等于一半．【分析】（1）根据M、N分别是AC、BC的中点，我们可得出MC、NC分别是AC、BC的一半，那么MC、CN的和就应该是AC、BC和的一半，也就是说MN是AB的一半，有了AC、CB的值，那么就有了AB的值，也就能求出MN的值了；（2）方法同（1）只不过AC、BC的值换成了AC+CB=a cm，其他步骤是一样的；（3）当C在线段AB的延长线上时，根据M、N分别是AC、BC的中点，我们可得出MC、NC分别是AC、BC的一半．于是，MC、NC的差就应该是AC、BC的差的一半，也就是说MN是AC-BC即AB的一半．有AC-BC的值，MN也就能求出来了．【详解】解：（1）∵、分别是、中点，且，，∴，∵， ∴（2）∵、分别是、的中点∴，又∵，∴(cm)总结为：在线段上时，长度为的一半（3）∵、分别是、中点∴,又∵，∴(cm)在线段所在直线上时就等于一半．【点睛】利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．18．填表见解析；（1）16，28，42；（2）二十八；（3）n，n+2，2n，3n；（4）a+c-b=2．【解析】试题分析：棱柱有两个面互相平行，其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行，边数为n的棱柱，有3n条棱，有2n个顶点，有(n+2)个面.试题解析：填表如下：（1）16    28    42.（2）二十八.（3）n    n+2    2n        3n.（4）a+c-b=2．点睛：首先要理解棱柱的组成，两个底面互相平行，侧面都是四边形，并且相邻两个四边形的公共边都互相平行，根据棱柱的构成则可以得到边数为n的棱柱的顶点数是：上底面的n个顶点+下底面的n个顶点=2n个；面数是：1个上底面+1个下底面+n个侧面=(n+2)个；棱数是：上下底面与侧面相交的棱有2n个+侧面相交的棱有n个=3n个.19．25cm或115cm．【解析】【分析】本题没有给出图形，在画图时，应考虑到A、B、M、N四点之间的位置关系的多种可能，再根据题意正确地画出图形解题．【详解】解：本题有两种情形：
（1）当A、C（或B、D）重合，且剩余两端点在重合点同侧时，

MN=CN-AM=CD-AB=70-45=25（厘米）；
（2）当B、C（或A、D）重合，且剩余两端点在重合点两侧时，

MN=CN+BM=CD+AB，=70+45=115（厘米）．
故两条线段的小圆孔之间的距离MN是25cm或115cm． 故答案为：25cm或115cm．【点睛】本题考查两点间的距离，在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．20．见解析【解析】解：如图所示：．视频21．（1）AC=32cm ；（2）OB=8cm．【分析】（1）由B在线段AC上可知AC＝AB＋BC，把AB＝24cm，BC＝AB＝8cm代入即可求出结论；（2）根据O是线段AC的中点及AC的长可求出CO的长，由OB＝CO−BC即可得出结果．【详解】解：（1）∵AB＝24cm，BC＝AB，∴BC＝8cm，∴AC＝AB＋BC＝24＋8＝32cm；（2）由（1）知：AC＝32cm，∵点O是线段AC的中点，∴CO＝AC＝×32＝16cm，∴OB＝CO−BC＝16−8＝8cm．【点睛】本题考查了与线段中点有关的计算问题，掌握线段的中点的性质、线段的和、差、倍的运算是解题的关键．22．见解析，原因是两点之间，线段最短【分析】结合侧面展开图，根据两点之间线段最短即可得出答案．【详解】解：沿着经过点A的圆柱的高将圆柱侧面展开成长方形，点B位于长方形长的中点处，联结，就是最短线，如图；理由是两点之间，线段最短．
【点睛】本题考查两点之间线段最短，属于基本题型．