初中人教版第十八章 平行四边形18.1 平行四边形18.1.1 平行四边形的性质课文课件ppt

这是一份初中人教版第十八章 平行四边形18.1 平行四边形18.1.1 平行四边形的性质课文课件ppt，共15页。PPT课件主要包含了两组对边分别平行等内容，欢迎下载使用。

你还能举出其他的例子吗？
情景引入 观察下图，平行四边形在生活中常见的图形.
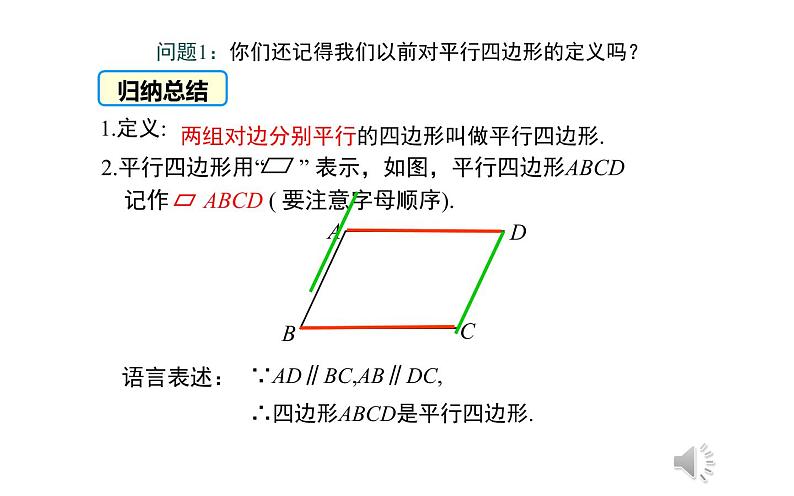
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示，如图，平行四边形ABCD 记作 ABCD ( 要注意字母顺序).
∵AD∥BC,AB∥DC,∴四边形ABCD是平行四边形.
问题1：你们还记得我们以前对平行四边形的定义吗？
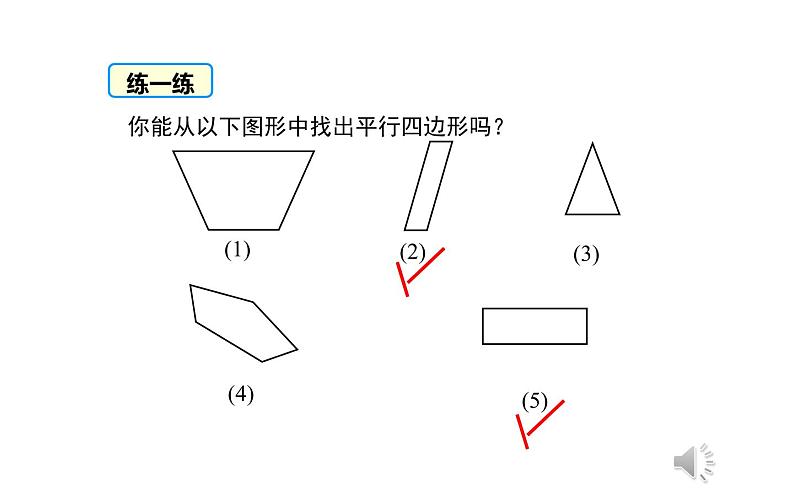
你能从以下图形中找出平行四边形吗？
探究画一个平行四边形，观察他除了“两组对边平行”以外，它的边之间，角之间还有什么关系？折叠或测量一下，和你的猜想一致吗？活动1 请用尺子等工具度量你手中平行四边形的四条边，并记录下数据，你能发现AB与DC，AD与BC之间的数量关系吗?测得AB= DC， AD=BC.
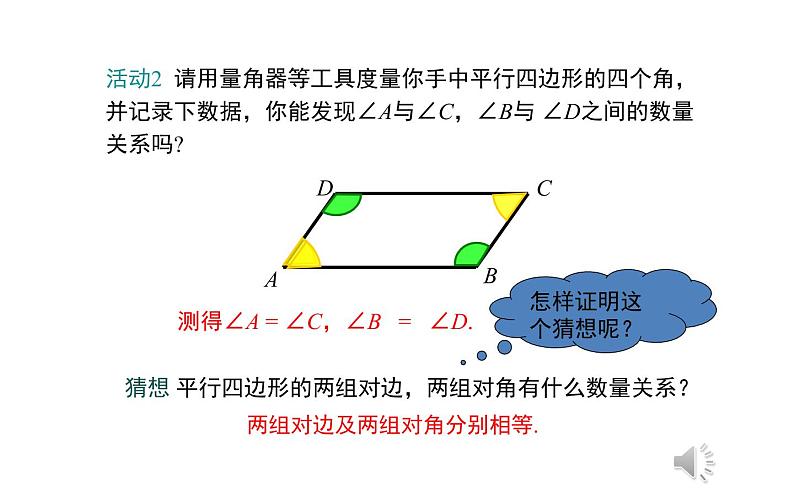
测得∠A = ∠C，∠B = ∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角，并记录下数据，你能发现∠A与∠C，∠B与 ∠D之间的数量关系吗?
猜想 平行四边形的两组对边，两组对角有什么数量关系？
两组对边及两组对角分别相等.
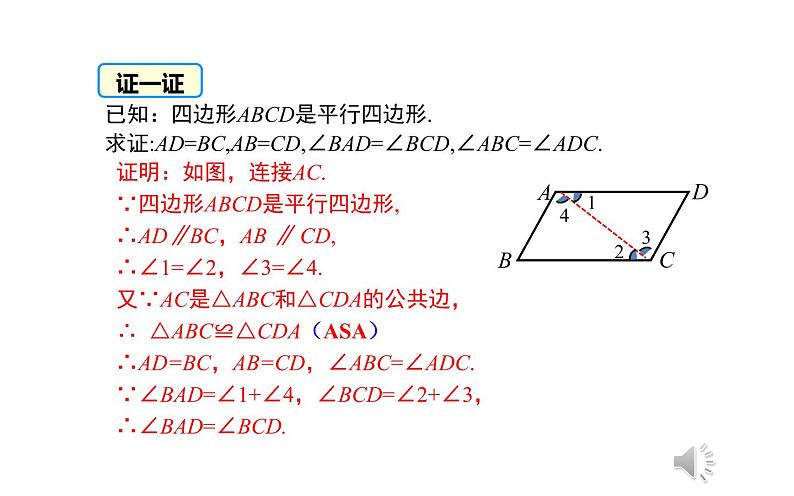
证明：如图，连接AC.∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠1=∠2，∠3=∠4.又∵AC是△ABC和△CDA的公共边，∴ △ABC≌△CDA（ASA）∴AD=BC，AB=CD，∠ABC=∠ADC.∵∠BAD=∠1+∠4，∠BCD=∠2+∠3，∴∠BAD=∠BCD.
已知：四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
思考 不添加辅助线，你能否直接运用平行四边形的定义，证明其对角相等？
证明：∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠A+∠B=180°，∠A+∠D=180°，∴∠B=∠D.同理可得∠A=∠C.
平行四边形的对边相等．平行四边形的对角相等．
平行四边形的性质除了对边互相平行以外，还有:
1.如图，在□ABCD中.
(1)若∠A=130°，则∠B=______ ，∠C=______ ， ∠D=______.
(3)若∠A+ ∠C= 200°，则∠A=_____，∠B=______.
(2)若AB=3,BC=5,则它的周长= ______.
证明： ∵四边形ABCD是平行四边形，∴ ∠A= ∠C，AD=CB.又∠AED= ∠CFB=90°，∴ △ADE≌△CBF（AAS）,∴AE=CF.
思考 在上述证明中还能得出什么结论？DE=BF归纳总结:两条平行线之间的平行线段相等
两条平行线间的距离相等.
若m // n，AB、CD、EF垂直于 n，交n于B、D、F，交 m于A、C、E.
同前面易得AB=CD=EF
两条平行线间的距离：两条平行线中，一条直线上任意一点到另一条直线的距离
如图，AB∥CD，BC⊥AB，若AB=4cm，S△ABC=12cm2，求△ABD中AB边上的高．
解：S△ABC = AB•BC,= ×4 ×BC=12cm2，∴BC=6cm.∵AB∥CD，∴点D到AB边的距离等于BC的长度，∴△ABD中AB边上的高为6cm．
课堂小结通过本节课的学习，你有什么收获和体会？
两组对边分别平行，相等
两条平行线间的距离相等
两组对角分别相等，邻角互补