高三数学第一轮复习 函数与方程教案 文

函数与方程

一、知识梳理：（阅读教材必修1第85页—第94页）

1、  方程的根与函数的零点

(1)  零点:对于函数,我们把使0的实数x叫做函数的零点。这样，函数的零点就是方程0的实数根，也就是函数的图象与x轴交点的横坐标，所以方程0有实根。

（2）、函数的零点存在性定理：如果函数在区间[a，b]上的图象是连续不断的一条曲线，并且有那么，在区间（a，b）内有零点，即存在c，使得=0，这个C 也就是方程0的实数根。

（3）、零点存在唯一性定理：如果单调函数在区间[a，b]上的图象是连续不断的一条曲线，并且有那么，在区间（a，b）内有零点，即存在唯一c，使得=0，这个C 也就是方程0的实数根。

（4）、零点的存在定理说明：

①求在闭间内连续，满足条件时，在开区间内函数有零点；

②条件的函数在区间（a，b）内的零点至少一个；

③间[a，b]上连续函数，不满足，这个函数在（a，b）内也有可能有零点，因此在区间[a，b]上连续函数，是函数在（a，b）内有零点的充分不必要条件。

2、  用二分法求方程的近似解

（1）、二分法定义：对于区间[a，b]连续不断且的函数通过不断把区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点的近似值的方法叫做二分法。

（2）、给定精确度（）用二分法求函数的零点近似值步骤如下：

①确定区间[a，b]，验证给定精确度（）；

②求区间（a，b）的中点c；

③计算

（I）若=0，则c就是函数的零点；

（II）若则令b=c，（此时零点）；

（III）若则令a=c，（此时零点）；

④判断是否达到精确度 ，若|a-b|，则得到零点的近似值a（或b），否则重复②--④步骤。

函数的零点与相应方程根的关系，我们可用二分法来求方程的近似解，由于计算量较大，而且是重复相同的步骤，因此，我们可以通过设计一定的程序，借助计算器或者计算机来完成计算。

二、题型探究

[探究一]：函数的零点是函数y＝f(x)与x轴的交点吗？是否任意函数都有零点？

提示：函数的零点不是函数y＝f(x)与x轴的交点，而是y＝f(x)与x轴交点的横坐标，也就是说函数的零点不是一个点，而是一个实数；并非任意函数都有零点，只有f(x)＝0有根的函数y＝f(x)才有零点．

[探究二]：若函数y＝f(x)在区间(a，b)内有零点，则y＝f(x)在区间[a，b]上的图象是否一定是连续不断的一条曲线，且有f(a)·f(b)<0呢？

提示：不一定．由图(1)(2)可知．

[探究三]：有二分法求方程的近似解

例1：已知图象连续不断的函数在区间（a，b）（b-a=0.1）上有唯一零点 ，如果用“二分法”求个零点（精确度0.0001）的近似值，那么将区间等分的次数至少是（D）

（A）7         （B）8       （C）9       （D）10

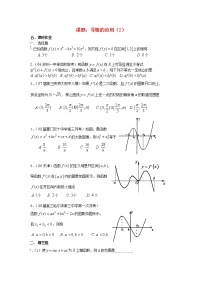
例2：下列图象不能用二分法示这个函数的零点的是（3、5）

二、              方法提升

1、  根据根的存在定量理，判断方程的根的取值范围是在高考题中易考的问题，这类问题只需将区间的两个端点的值 代入计算即可判断出来。、

2、  判断函数零点的个数问题常数形结合的方法，一般将题止听等 式化为两个函数图象的交点问题。

3、  在导数问题中，经常在高考题中出现两个函数图象的交点的个数问题，要确定函数具体的零点的个数需逐个判断，在符合根的存在定量的条件下，还需辅以函数的单调性才能准确判断出零点的个数。

三、反思感悟：
                                                                        

                                                                         。

五、课时作业：

1．函数的零点个数（  C  ）.

    A. 0个       B. 1个        C. 2个           D. 不能确定

2．若函数在内恰有一解，则实数的取值范围是（ B   ）.

    A.     B.     C.       D.

3．函数的零点所在区间为（  C  ）

    A. （1，0）     B. （0，1）    C. （1，2）    D. （2，3）

4．方程lgx＋x＝0在下列的哪个区间内有实数解（ B   ）.

    A. [-10，-0.1]     B.        C.         D.

5．函数的图象是在R上连续不断的曲线，且，则在区间上（ D  ）.

    A. 没有零点   B. 有2个零点   C. 零点个数偶数个  D. 零点个数为k，

6、设若关于的方程有三个不同的实数解，则等于（ A  ）    A.5      B.    C.13      D.

7、是定义在上的奇函数，其图象如下图所示，

令，则下列关于的叙述正确的是（ B   ）
A．若，则函数的图象关于原点对

B．若，则方程=0有大于2的实根

C．若，则方程=0有两个实根

D．若，则方程=0有三个实根

8、已知是以2为周期的偶函数，当时，，那么在区间内，关于的方程（其中走为不等于l的实数）有四个不同的实根，则的取值范围是（C  ）

A．   B．  C．   D．

9、定义在R上的函数既是奇函数，又是周期函数，是它的一个正周期.若将方程在闭区间上的根的个数记为，则可能为（ D ）

       A.0              B.1             C.3               D.5  

10、已知是定义在上的奇函数，其图象关于对称且，则方程 在内解的个数的最小值是 (D  )     

       A．       B．              C．          D．

11、已知以为周期的函数,其中｡若方程恰有5个实数解,则的取值范围为( B   )

   A.  B.          C.  D.

12、方程的解所在的区间为( C )  

  A.(0,1)              B.(1,2)             C.(2,3)          D.(3,4)

13、函数的零点所在的区间是(  B  )

A             B            C         D

14、若方程的根在区间上，则的值为( C )

A．   B．1    C．或1    D．或2

15、设函数则(D)

A.在区间内均有零点｡               B.在区间内均无零点｡

C.在区间内有零点,在区间内无零点｡ D.在区间内无零点,在区间内有零点｡

16、设方程 的两个根为，则 （D  ）

A          B        C       D

17、已知则方程f(x)=2的实数根的个数是(  D )

A.0         B.1         C.2         D.3

18、已知函数在区间上有最小值,则函数在区间上是( C)     A.有两个零点     B.有一个零点        C.无零点         D.无法确定

19、已知是的零点，且，则实数a、b、m、n的大小关系是（ A  ）     

  A．  B．C．  D．

20、关于的方程，给出下列四个命题：

①存在实数，使得方程恰有2个不同的实根；②存在实数，使得方程恰有4个不同的实根；

③存在实数，使得方程恰有5个不同的实根；④存在实数，使得方程恰有8个不同的实根；

其中假命题的个数是( A   )     A．0    B．1    C．2    D．3

21、条件:;条件:函数在区间上存在,使得成立,则是的 (A ) 

A.充分非必要条件B.必要非充分条件   C.充分必要条件  D.既非充分也非必要条件

22、ax2+2x+1=0至少有一个负实根的充要条件是(  C  )
A.0<a≤1                  B.a<1              C.a≤1       D.0<a≤1或a<0

23、已知函数在（1，2）有一个零点则实数的值范围是 （A ）
A.        B.        C. 或      D.

二、填空题

24．函数的零点是   2或3     . 

25、若函数f(x)=a-x-a(a>0且a1)有两个零点,则实数a的取值范围是_a>1___.

26、若函数f(x)=ex-2x-a在R上有两个零点，则实数a的取值范围是_a>2-2ln2_

27．函数零点的个数为   3     .

28、定义域和值域均为（常数）的函数

和的图像如图所示，给出下列四个命题：

（1）方程有且仅有三个解；

（2）方程有且仅有三个解；

（3）方程有且仅有九个解；

（4）方程有且仅有一个解。

那么，其中正确命题的个数是__(1)(4)___ 。

三、解答题

29.已知二次方程的两个根分别属于(-1,0)和(0,2),求的取值范围.

 解：设=，则=0的两个根分别属于(-1,0)和(1,2).

所以，即，    ∴  ． 

30．已知：

（1）为何值时，函数的图象与轴有两个零点；

解：（1），解得且.

（2）如果函数两个零点在原点左右两侧，求实数的取值范围.

或.  解得.

31、设关于的函数R），
（1）若函数有零点，求实数b的取值范围；
（2）当函数有零点时，讨论零点的个数，并求出函数的零点.

解：（1）原函数零点的问题等价于方程

化简方程为，

的解为；

综合①、②，得1）当时原方程有两解：；

2）当时，原方程有唯一解；3）当时，原方程无解。  

32、已知a是实数，函数，如果函数在区间[-1，1]上有零点，求实数a的取值范围。

解析1：函数在区间[-1，1]上有零点，即方程=0在[-1，1]上有解，

   a=0时，不符合题意，所以a≠0,方程f(x)=0在[-1，1]上有解<=>或或或或a≥1　

所以实数a的取值范围是或a≥1　

解析2：a=0时，不符合题意，所以a≠0,又

∴=0在[-1，1]上有解，在[-1，1]上有解在[-1，1]上有解，问题转化为求函数[-1，1]上的值域；设t=3-2x，x∈[-1，1]，则，t∈[1,5],，

设，时，，此函数g(t)单调递减，时，>0,此函数g(t)单调递增，∴y的取值范围是，∴=0在[-1，1]上有解∈或。

补充练习：

1、已知函数y=f(x)（x∈R）满足f(x+1)=f(x—1)，且x∈[—1，1]时，f(x)=x2，则y=f(x)与y=log5x的图象的交点个数为             

2、是定义在R上的以3为周期的奇函数，且，则方程在区间 内解的个数的最小值是(  )           A．2      B．3     C．4      D．5

3、函数在内恰有一个零点，则实数的取值范围是（   ）

4、函数的零点一定位于下列哪个区间（    ）.

A.          B.         C.        D.

5、在区间[3，5]上有零点的函数是  （     ）

A．  B．     C．  D．

6、函数在区间［0，］上的零点个数为（    ）

   A．1个              　B．2个               C．3个             D．4个

7、设函数，有               （    ）
A．在定义域内无零点；                 B．存在两个零点，且分别在、内；
C．存在两个零点，且分别在、内；D．存在两个零点，都在内。

8、已知是使表达式成立的最小整数，则方程实数根的个数为（ ）

（A）0     （B）1    （C）2    （D）3

9、已知函数（为自然对数的底），下列判断中正确的是（   ）

A．函数无零点；        B．函数有且只有一个零点，且该零点在区间内；

C．函数有两个零点，其中一个为正数，另一个为负数；

D．函数有且只有一个零点，且该零点在区间内。

10、若函数的零点与的零点之差的绝对值不超过0.25， 则可以是( )

A.   B.   C.    D.

11、已知函数，若实数是方程的解，且，则的值为( )

A．恒为正值  B．等于  C．恒为负值 D．不大于

12、定义域为R的函数，若关于的方程恰有5个不同的实数解，则（     ）

A．              B．                C．                   D．

13、方程恰有两个不相等实根的充要条件是            

14、已知二次函数的导函数的图像与直线平行，且在处取得极小值．设．

（1）若曲线上的点到点的距离的最小值为，求的值；

（2）如何取值时，函数存在零点，并求出零点．           

15、设函数

（Ⅰ）当曲线处的切线斜率

（Ⅱ）求函数的单调区间与极值；

（Ⅲ）已知函数有三个互不相同的零点0，，且。若对任意的，恒成立，求m的取值范围。

补充练习答案解析:1、4 ;2、D; 3、D; 4、B;5、A ; 6、B;7、D ;8、C;9、B ;10、A;11、A;12、B; 13、;14、解：（1）依题可设 ()，则；   又的图像与直线平行      即   ， ，  

设，则  

当且仅当时，取得最小值，即取得最小值

当时，   解得

当时，   解得

  （2）由()，得  

当时，方程有一解，函数有一零点；

当时，方程有二解，

若，，函数有两个零点，即；若，，函数有两个零点，即；

当时，方程有一解,   ,

函数有一零点

综上，当时, 函数有一零点；

当()，或（）时，

函数有两个零点；

当时，函数有一零点.

15、【解析】解：当

所以曲线处的切线斜率为1.

（2）解：，令，得到

因为

当x变化时，的变化情况如下表：

在和内减函数，在内增函数。

函数在处取得极大值，且=

函数在处取得极小值，且=

（3）解：由题设，

所以方程=0由两个相异的实根，故，且，解得，因为

若，而，不合题意

若则对任意的有则又，所以函数在的最小值为0，于是对任意的，恒成立的充要条件是,解得 。，综上，m的取值范围是