



专题02 函数基本性质-2021届新高考数学一轮复习知识点总结与题型归纳面面全
展开一、函数的概念
1. 映射
设A,B是两个非空集合,如果按照某种对应法则f,对A中的任意一个元素x在B中有一个且仅有一个元素y与x对应,则称f是集合A到集合B的映射,这时称y是x在映射f的作用下的象,记作f(x),于是
y=f(x)
x称为y的原象,映射f也可记为:
f:A→B
x→f(x)
其中A叫做映射f的定义域(函数定义域的推广).由所有象f(x)构成的集合叫做映射f的值域.通常记作f(A).
将上述定义中集合A、B限制为非空数集,便可以得到函数的概念,如下:
2. 函数
设集合A是一个非空数集,对A中的任意的数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种对应关系叫做集合A上的一个函数.记作y=f(x),x∈A
其中x叫做自变量.自变量取值的范围(数集A)叫做这个函数的定义域.
如果自变量取值a,则由法则f确定的值y称为函数在a处的函数值,记作y=f(a)
所有函数值构成的集合{yy=f(x) , x∈A}叫做这个函数的值域.
3. 函数的三要素:定义域,值域,对应法则
4. 函数的表示法
(1)解析法:就是把两个变量的函数关系,用一个等式来表示,这个等式叫做函数的解析表达式,简称解析式;
(2)列表法:就是列出表格来表示两个变量的函数关系;
(3)图象法:就是用函数图象表示两个变量之间的关系.
二、函数的定义域
1. 基本函数的定义域
(1)分式的分母不应为零;
(2)零次或负次指数次幂的底数不为零;
(3)偶次方根的被开方数大于或者等于零;
(4)对数式的真数大于零;
(5)底数大于0且不等于1;
(6)f(x)=tanx的定义域为{x|x≠kπ+π2 , k∈Z};
(7)应用题中要结合实际情况考察定义域.
2. 抽象函数的定义域
抽象函数的定义域:在同一对应法则f下,括号内的作用对象取值范围必须一致,但要注意的是括号内的部分同样作为函数也有它本身的定义域,因此需要两部分求解后取交集.
三、函数的解析式
1. 换元法求解析式
2. 解方程组法求解析式
3. 待定系数法求解析式
四、函数的值域
1. 利用函数单调性
2. 模型函数的应用
(1)二次型
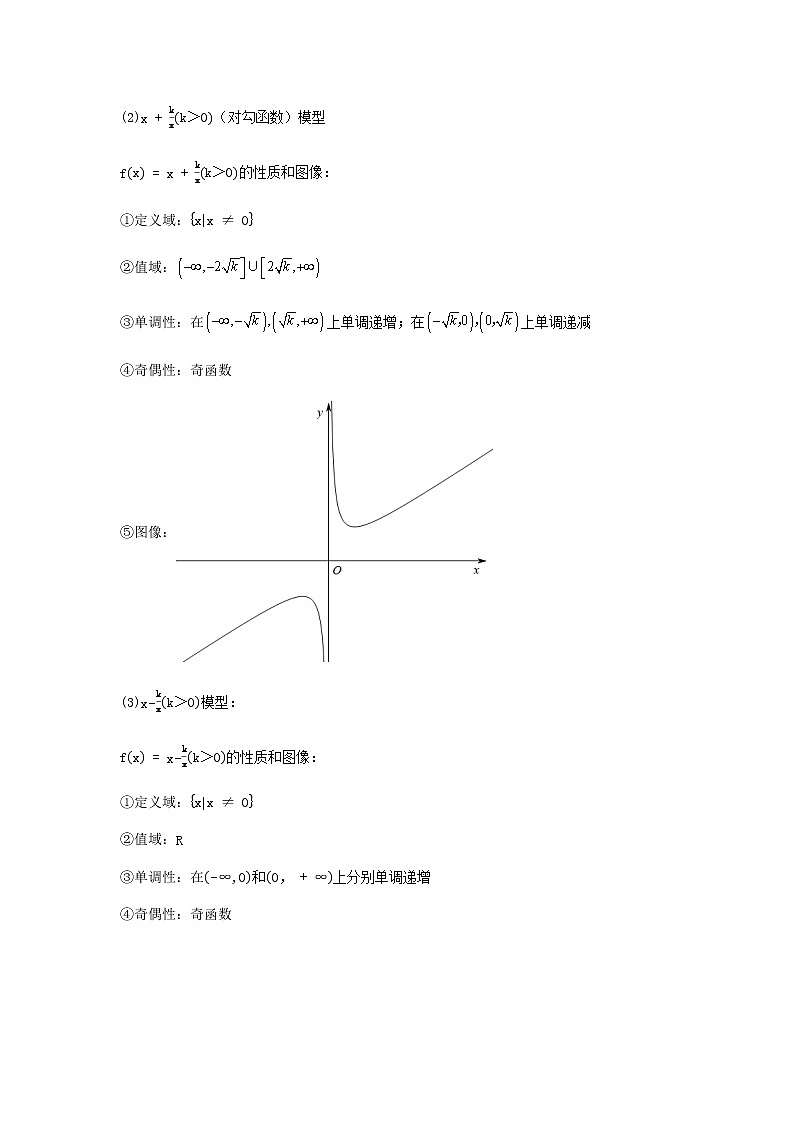
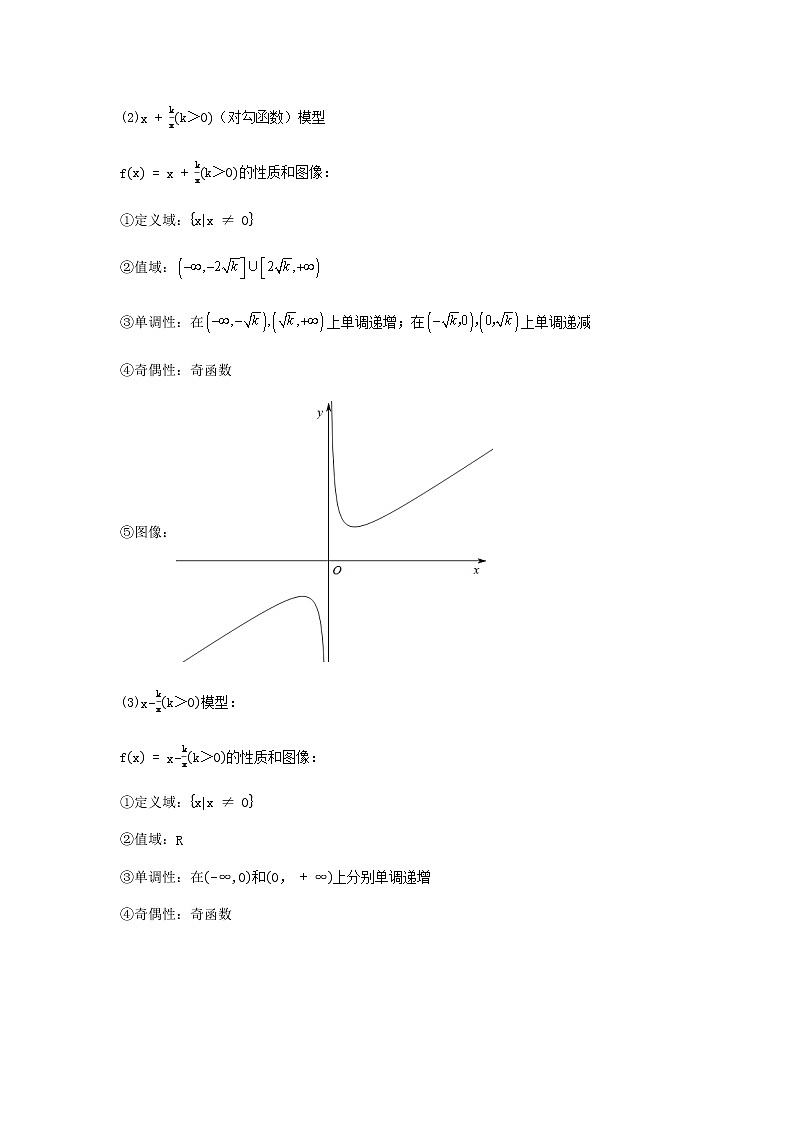
(2)x+kxk>0(对勾函数)模型
fx=x+kxk>0的性质和图像:
①定义域:xx≠0
②值域:
③单调性:在上单调递增;在上单调递减
④奇偶性:奇函数
⑤图像:
(3)x−kxk>0模型:
fx=x−kxk>0的性质和图像:
①定义域:xx≠0
②值域:R
③单调性:在−∞,0和0,+∞上分别单调递增
④奇偶性:奇函数
⑤图像:
3. 分离常数
4. 换元(代数换元和三角换元)
5. 基本不等式
6. 几何法
典例精讲
【典例1】已知函数f(x)=ex﹣e﹣x﹣2x+1,若对于任意实数x,不等式f(x2+a)+f(2ax)>2恒成立,则实数a的取值范围是( )
A.(0,1]B.(﹣1,1)C.(0,1)D.(0,2)
【典例2】若函数的值域为,则的取值范围是
A.,B.C.,D.
【典例3】设f(x)=ln((x+1)2+1+x+1)﹣2,若f(a)=1,f(b)=﹣5,则a+b=( )
A.2B.0C.1D.﹣2
【典例4】已知集合A=N*,B={a|a=2n﹣1,n∈Z},映射f:A→B,使A中任一元素a与B中元素2a﹣1对应,则与B中元素17对应的A中元素是( )
A.3B.5C.17D.9
【典例5】函数f(x)=(x2﹣4x+3)sin(x﹣2)+3x在区间[﹣1,5]的最大值和最小值分别为a,b,则a+b=( )
A.0B.﹣12C.6D.12
【典例6】已知函数f(x)=lg2x+1的定义域为[1,2],g(x)=f2(x)+f(x2)+m,若存在实数a,b,c∈{y|y=g(x)},使得a+b<c,则实数m的取值范围是( )
A.m<−74B.m<2C.m<3D.m<14
【典例7】若函数f(x)=1ex−x+m的定义域为R,则实数m的取值范围是 .
【典例8】设函数f(x)=2−2x+4和函数g(x)=ax+a﹣1,若对任意x1∈[0,+∞)都有x2∈(﹣∞,1]使得f(x1)=g(x2),则实数a的取值范围为 .
考点2:函数的性质
一、函数的单调性
1. 定义:设函数y=f(x)的定义域为A,区间M⊆A,如果取区间M中任意两个值,x1,x2,改变量△x=x2−x1>0,则当△y=y2−y1>0时,就称函数y=f(x)在区间M上是增函数.则当△y=y2−y1<0时,就称函数y=f(x)在区间M上是增函数.
2. 说明:讨论函数单调性必须在其定义域内进行,因此要研究函数单调性必须先求函数的定义域,函数的单调区间是其定义域的子区间;
3. 判断函数的单调性的方法有:
(1)定义法;
(2)利用已知函数的单调性;
(3)利用函数的导数判断函数的单调性;
(4)复合函数的单调性结论:“同增异减”;
(5)奇函数在其对称的单调区间内有相同的单调性,偶函数在其对称的单调区间内具有相反的单调性.
(6)在公共定义域内,增函数f(x)+增函数g(x)是增函数;减函数f(x)+减函数g(x)是减函数;增
函数f(x)−减函数g(x)是增函数;减函数f(x)−增函数g(x)是减函数.
(7)af(x)当a>0时候与g(x)的单调性相同,当a<0时候与g(x)的单调性相反.
(8)如果f(x)是单调函数且f(x)>0,则f(x)和1f(x)数的单调性是相反的,如果f(x)是单调函数且f(x)<0,f(x)和1f(x)的单调性是相反的.
二、函数的奇偶性
1. 定义
奇函数:设函数y=f(x)的定义域为D,如果对D内的任意一个x都有f(−x)=−f(x),则这个函数叫做奇函数.
偶函数:设函数y=f(x)的定义域为D,如果对D内的任意一个x都有f(−x)=f(x),则这个函数叫做偶函数.
2. 判断函数奇偶性的方法
(1)定义法
先求函数的定义域,若函数的定义域部关于原点对称,则此函数不具有奇、偶性;若函数定义域关于原点对称;在判断f(x)与f(−x)关系;若f(−x)=f(x),则f(x)是偶函数;若f(−x)=−f(x),则f(x)是奇函数.
(2)图像法
函数图像关于y轴对称⇔函数是偶函数.函数图像关于原点对称⇔函数是奇函数.
3. 函数奇偶性的性质
(1)若奇函数f(x)的定义域包含0,则f(0)=0.
(2)奇函数在对称的单调区间内有相同的单调性,偶函数在对称的单调区间内具有相反的单调性.
设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域D=D1∩D2上:奇±奇=奇,偶±偶=偶,奇×奇=偶(例如y=xsinx是偶函数),偶×偶=偶,奇×偶=奇(例如y=xcsx是奇函数).
三、函数的周期性
1. 判断一个函数是否是周期函数要抓住两点:
一是对定义域中任意的x恒有f(x+T)=f(x);二是能找到适合这一等式的非零常数T,一般来说,周期函数的定义域均为无限集.
2. 具有周期性的抽象函数:
函数y=fx满足对定义域内任一实数x(其中a为常数),
(1)函数y=f(x)满足f(a+x)=f(a−x)(a>0),若f(x)为奇函数,则其周期为T=4a,若f(x)为偶函数,则其周期为T=2a.
(2)函数y=f(x) x∈R的图象关于直线x=a和x=ba
(4)函数y=f(x) x∈R的图象关于Aa,y0和直线x=b a
(5)关于函数的周期性有如下推广结论:
若函数y=fx满足如下关系,则fx的周期为2T
= 1 \* GB3 ①fx+T=−fx
= 2 \* GB3 ② fx+T=±1fx
= 3 \* GB3 ③fx+T2=±1+fx1−fx
= 4 \* GB3 ④fx+T2=±1−fx1+fx
四、函数的对称性
1. 一个函数fx的自对称问题:
(1)关于y轴对称⇔f(−x)=f(x);
(2)关于原点对称⇔f(−x)=−f(x);
(3)关于直线x=a对称⇔f(a+x)=f(a−x)或f(x)=f(2a−x);
(4)关于点(a,b)对称⇔f(x)=2b−f(2a−x)或f(a+x)−b=b−f(a−x).
2. 两个函数的互对称问题:
(1)y=fx与y=−fx关于x轴对称.
(2)y=fx与y=f−x关于y轴对称.
(3)y=fx与y=−f−x关于原点对称.
(4)y=fx与y=2a−fx关于y=a轴对称.
(5)y=fx与y=f2a−x关于x=a轴对称.
(6)y=fx与y=2b−f2a−x关于a,b对称.
(7)函数y=f(a−x)与y=f(x−b)的图像关于直线x=a+b2对称.
典例精讲
【典例1】设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则( )
A.f(lg314)>f(2−32)>f(2−23)
B.f(lg314)>f(2−23)>f(2−32)
C.f(2−32)>f(2−23)>f(lg314)
D.f(2−23)>f(2−32)>f(lg314)
【典例2】已知函数f(x)的定义域是[0,3],g(x)与f(x)的图象关于点(1,0)成中心对称,若g(ax)在[13,12]上有意义,则实数a的取值范围是( )
A.[﹣3,4]B.[﹣3,6]C.[﹣2,4]D.[﹣2,6]
【典例3】已知偶函数满足:对任意的,,,都有成立,则满足的取值范围是
A.B.C.D.
【典例4】若函数exf(x)(e≈2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为 .
①f(x)=2﹣x②f(x)=3﹣x③f(x)=x3④f(x)=x2+2.
【典例5】若函数f(x)=asin(x+π6)+3sin(x−π3)是偶函数,则实数a的值为 .
【典例6】设是定义在上以2为周期的偶函数,当,时,,则,时,的解析式为
A.B.C.D.
【典例7】已知f(x)是定义在R上的偶函数,且在区间(﹣∞,0)上单调递增,若实数a满足f(2|a﹣1|)>f(−2),则a的取值范围是 .
综合练习
1.函数f(x)=x+3+(2x+3)03−2x的定义域是( )
A.[﹣3,32]B.[﹣3,−32)∪(−32,32)
C.[﹣3,32)D.[﹣3,−32)∪(−32,32]
2.设集合M={x|0≤x≤2},N={y|0≤y≤2}.下列四个图象中能表示从集合M到集合N的函数关系的有( )
A.0个B.1个C.2个D.3个
3.已知是定义在上的奇函数,当时,,则
4.若函数y=f(x)的图象的一部分如图(1)所示,则图(2)所对应的函数解析式可以是( )
A.y=f(2x−12)B.y=f(2x﹣1)
C.y=f(12x−12)D.y=f(12x−1)
5.已知集合A={﹣1,0,1},B={0,1,2,3,4},f:x→y是集合A到B的映射,则下列对应法则可能成立的是( )
A.y=3xB.y=x2C.y=2xD.y=2x+1
6.函数是定义在上的偶函数,且(2),对任意的,都有,则 1 .
7.函数y=lg12(4x−2)的定义域是 .
8.已知函数f(x)=(2−a)x,x>12x−1,x≤1的值域为(﹣1,+∞),则a的取值范围是
9.设f为(0,+∞)→[0,+∞)的函数,对于任意正实数x,f(x)=3f(3x),当1≤x≤3时,f(x)=27﹣27|x﹣2|,则使得f(x)=23成立的最大实数x为 .
专题28 复数-2021届新高考数学一轮复习知识点总结与题型归纳面面全: 这是一份专题28 复数-2021届新高考数学一轮复习知识点总结与题型归纳面面全,文件包含专题28复数原卷版docx、专题28复数解析版docx等2份学案配套教学资源,其中学案共19页, 欢迎下载使用。
专题26 算法-2021届新高考数学一轮复习知识点总结与题型归纳面面全: 这是一份专题26 算法-2021届新高考数学一轮复习知识点总结与题型归纳面面全,文件包含专题26算法原卷版docx、专题26算法解析版docx等2份学案配套教学资源,其中学案共36页, 欢迎下载使用。
专题21 圆锥曲线的定义性质与结论-2021届新高考数学一轮复习知识点总结与题型归纳面面全: 这是一份专题21 圆锥曲线的定义性质与结论-2021届新高考数学一轮复习知识点总结与题型归纳面面全,文件包含专题21圆锥曲线的定义性质与结论原卷版docx、专题21圆锥曲线的定义性质与结论解析版docx等2份学案配套教学资源,其中学案共32页, 欢迎下载使用。












