

数学17.1 勾股定理精品练习
展开17.1勾股定理 同步习题
一.选择题
1.在Rt△ABC中,∠C=90°,a=1,c=2,则b的长是( )
A. B.2 C.1 D.
2.如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=15cm,其斜边上的高为( )
A.17cm B.8.5cm C.cm D.cm
3.如图所示,在△ABC中,AB=AC=5,AD⊥BC于点D,AD=4,则△ABC的面积为( )
A.6 B.12 C.24 D.36
4.如图,在等腰△ABC中,AB=AC=5,BC=6,腰上的高BE=4.8,则底边上的中线AD的长为( )
A.3.6 B.4 C.4.2 D.4.5
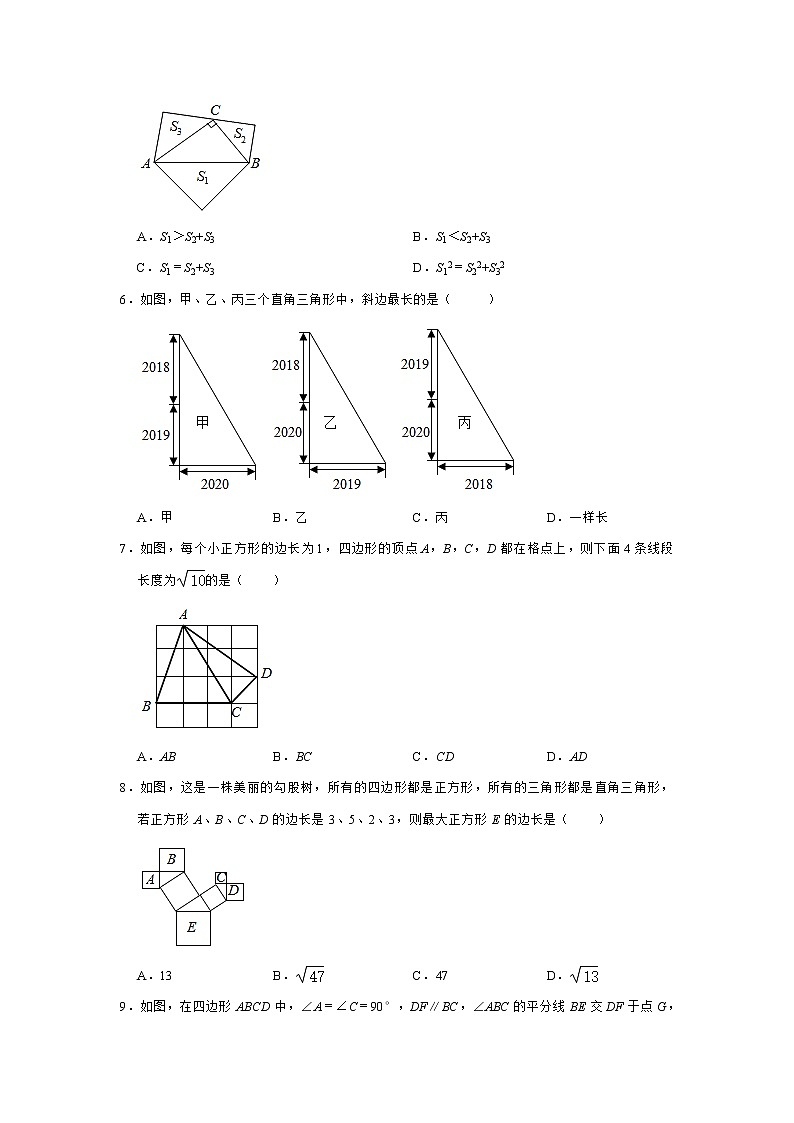
5.如图,△ABC中,∠ACB=90°,分别以三边为底向形外作等腰直角三角形,它们的面积依次为S1、S2、S3,则下列关系式正确的是( )
A.S1>S2+S3 B.S1<S2+S3
C.S1=S2+S3 D.S12=S22+S32
6.如图,甲、乙、丙三个直角三角形中,斜边最长的是( )
A.甲 B.乙 C.丙 D.一样长
7.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则下面4条线段长度为的是( )
A.AB B.BC C.CD D.AD
8.如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是( )
A.13 B. C.47 D.
9.如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )
A.1 B.2 C.3 D.4
10.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边中点,连接DE交AC于F,若CD=1,则AF=( )
A. B. C. D.
二.填空题
11.如图,在Rt△ABC中,∠C=90°,点D在BC上,且AC=DC=AB,若AD=,则BD= .
12.等腰△ABC中,AB=AC=4,∠BAC=30°,以AC为边作等边△ACD,则点B到CD的距离为 .
13.为了比较与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,D在BC上且BD=AC=1,通过计算可得 .(填“>”或“<”或“=”).
14.如图,△ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连PC.
(1)线段PC的最小值是 .
(2)当PC=5时,AP长是 .
15.如图,在Rt△ABC中,∠ACB=90°,AB=3,BC=2,∠ABC的平分线BD交AC于点E,若BC=CD,则△ABE的面积为 .
三.解答题
16.已知Rt△ABC的边长为a、b、c,其中c为斜边,且a、b满足+=0,求c的值.
17.如图,四边形ABCD中,AB⊥AD,已知AD=6cm,AB=8cm,CD=24cm,BC=26cm,求四边形ABCD的面积.
18.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.
(1)在Rt△ABC中,AC=m,BC=n,∠ACB=90°,若图①中大正方形的面积为61,小正方形的面积为1,求(m+n)2;
(2)若将图①中的四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,求这个风车的外围周长(图中实线部分).
参考答案
一.选择题
1.解:在Rt△ABC中,∠C=90°,a=1,c=2,
∴b===.
故选:D.
2.解:在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=15cm,由勾股定理得到:AB==17cm;
由AC•BC=CD•AB得到:CD===(cm),
故选:D.
3.解:∵如图所示,在△ABC中,AB=AC=5,AD⊥BC于点D,
∴BD=CD,BC=2BD.
在直角△ABD中,AB=5,AD=4,则由勾股定理得到:BD===3.
∴BC=2BD=6.
∴△ABC的面积为:BC•AD==12.
故选:B.
4.解:方法1:如图,∵在等腰△ABC中,AB=AC=5,BC=6,AD是底边上的中线,
∴AD⊥BC,且BD=CD=3,
在直角△ABD中,由勾股定理得到:AD===4.
方法2:依题意有:BC•AD=AC•BE,
即×6AD=×5×4.8,
解得AD=4.
故选:B.
5.解:如右图所示,
△ABC中,∠ACB=90°,分别以三边为底向形外作等腰直角三角形,
∴S1==,
同理可得,S2=,S3=,
∵∠ACB=90°,
∴a2+b2=c2,
∴S1=S2+S3,
故选:C.
6.解:由勾股定理可知甲、乙、丙三个直角三角形中,斜边的平方分别为:
甲:(2018+2019)2+20202;
乙:(2018+2020)2+20192;
丙:(2019+2020)2+20182.
∵(2018+2019)2+20202﹣[(2018+2020)2+20192]
=40372+20202﹣40382﹣20192
=(40372﹣40382)+(20202﹣20192)
=(4037+4038)(4037﹣4038)+(2020+2019)(2020﹣2019)
=﹣8075+4039
=﹣4036<0,
∴甲的斜边的小于乙的斜边;
∵(2018+2020)2+20192﹣[(2019+2020)2+20182]
=40382+20192﹣40392﹣20182
=(40382﹣40392)+(20192﹣20182)
=(4038+4039)(4038﹣4039)+(2019+2018)(2019﹣2018)
=﹣8077+4037
=﹣4040
<0,
∴乙的斜边的小于丙的斜边,
∴斜边最长的是丙.
故选:C.
7.解:AB==,BC=3,CD==,AD==,
故长度为的线段是AB,
故选:A.
8.解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:
x2=32+52=34;
y2=22+32=13;
z2=x2+y2=47;
即最大正方形E的面积为:z2=47,边长为z=.
故选:B.
9.解:过E作EM⊥BC,交FD于点N,
∵DF∥BC,
∴EN⊥DF,
∴EN∥HG,
∴∠DEN=∠DHG,∠END=∠HGD,
∴△END∽△HGD,
∴=,
∵E为HD中点,
∴=,
∴=,即HG=2EN,
∴∠DNM=∠NMC=∠C=90°,
∴四边形NMCD为矩形,
∴MN=DC=2,
∵BE平分∠ABC,EA⊥AB,EM⊥BC,
∴EM=AE=3,
∴EN=EM﹣MN=3﹣2=1,
则HG=2EN=2.
故选:B.
10.解:∵∠DAB=60°,AC平分∠DAB,
∴∠CAB=DAB=30°,
∵∠B=60°,
∴∠CAB+∠B=90°,
∴∠ACB=90°,
∵CD=1,
∴AC=2,AD=,
∵∠DAC=∠CAB,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴=,
∴AB==,
连接CE,
∵E为AB边中点,
∴CE=AB=AE=,
∴∠EAC=∠ECA;
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
∴△AFD∽△CFE,
∴=,
∴=,
∴AF=,
故选:A.
二.填空题
11.解:∵AD=,∠C=90°,AC=DC,
∴AC=CD=1,
∵AC=DC=AB,
∴AB=2,
∴BC==,
∴BD=﹣1,
故答案为:﹣1.
12.解:当点D在AC的左侧时,设AB与CD交于点E,
∵△ACD是等边三角形,
∴AC=AD=CD=4,∠DAC=60°,
又∵∠BAC=30°,
∴∠DAE=∠BAC=30°,
∴AB⊥CD,
∵∠BAC=30°,
∴CE=AC=2,AE=EC=2,
∴BE=AB﹣AE=4﹣2;
当点D在AC的右侧时,过点B作BE⊥CD,交DC的延长线于点E,连接BD,
∵△ACD是等边三角形,
∴AC=AD=CD=AB=4,∠DAC=60°,
∴∠BAD=90°,
∴BD===4,
∵AB=AC,∠BAC=30°,
∴∠ACB=75°,
∴∠BCE=180°﹣∠ACD﹣∠ACB=45°,
∵BE⊥CE,
∴∠BCE=∠CBE=45°,
∴BE=CE,
∵BD2=BE2+DE2,
∴32=BE2+(CE+4)2,
∴BE=2﹣2,
综上所述:点B到CD的距离为2﹣2或4﹣2.
13.解:∵∠C=90°,BC=3,BD=AC=1,
∴CD=2,AD==,AB==,
∴BD+AD=+1,
又∵△ABD中,AD+BD>AB,
∴+1>,
故答案为:<.
14.解:(1)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB===10,
由垂线段最短得:当PC⊥AB时,PC的值最小,
此时,△ABC的面积=•AB•PC=•AC•BC,
∴AB•PC=AC•BC,
∴PC===4.8,
故答案为:4.8;
(2)过C作CQ⊥BC于Q,如图所示:
同(1)得:CQ=4.8,
由勾股定理得:AQ===3.6,PQ===1.4,
当P在线段BQ上时,AP=AQ+PQ=3.6+1.4=5;
当P在线段AQ上时,AP=AQ﹣PQ=3.6﹣1.4=2.2;
综上所述,AP的长为5或2.2,
故答案为:5或2.2.
15.解:在Rt△ABC中,∠ACB=90°,AB=3,BC=2,
∴AC===,
∴△ABC的面积为:BC×AC=×2×=.
∵BD平分∠ABC,
∴∠ABE=∠CBE.
∵BC=CD,
∴CD=2,∠CBE=∠CDE,
∴∠ABE=∠CDE,
∴AB∥CD,
∴△ABE∽△CDE,
∴AE:CE=AB:CD=3:2,
∴△ABE的面积为:×=.
故答案为:.
三.解答题
16.解:∵+=0,
∴=0,且=0,
∴a=3,b=4.
由勾股定理得,c==5.
所以c的值是5.
17.解:∵AB⊥AD,
∴∠A=90°,
∴△ABD为直角三角形,
∵BD2=AB2+BD2=82+62=102,
∴BD=10,
在△BCD中,
∵DC2+BD2=BC2,
∴△BCD为直角三角形,且∠BDC=90°,
∴S四边形ABCD=S△BCD﹣S△ABD=×10×24﹣×6×8=96(cm2).
18.解:(1)由题意(n﹣m)2=1,m2+n2=61,
∴2mn=60,
∴(m+n)2=m2+n2+2mn=61+60=121;
(2)由(1)可知,
∴,
∴AC=5,BC=6,
∵∠ACB=90°,AC=5,CD=12,
∴AD===13,
∴这个风车的外围周长=4(13+6)=76.
初中数学人教版八年级下册17.1 勾股定理同步训练题: 这是一份初中数学人教版八年级下册17.1 勾股定理同步训练题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理同步达标检测题: 这是一份初中数学人教版八年级下册17.1 勾股定理同步达标检测题,共13页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理课后作业题: 这是一份初中数学人教版八年级下册17.1 勾股定理课后作业题,共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













