





还剩37页未读,
继续阅读
成套系列资料,整套一键下载
人教版中考数学第一轮考点过关:第六单元圆课时24与圆有关的位置关系
展开
这是一份人教版中考数学第一轮考点过关:第六单元圆课时24与圆有关的位置关系,共45页。PPT课件主要包含了垂直于,垂直平分线,角平分线,考向一切线的性质,考向二切线的判定等内容,欢迎下载使用。
课时24 与圆有关的位置关系
点与圆的位置关系 直线与圆的位置关系 切线的判定和性质 三角形(多边形)的内切圆
考点一 点与圆的位置关系
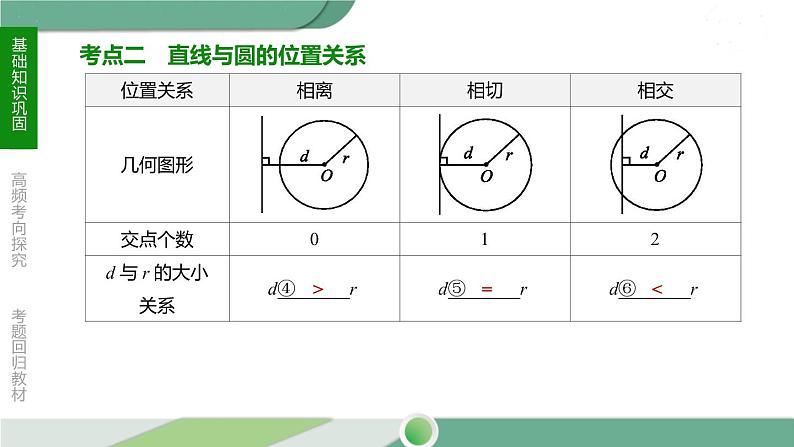
考点二 直线与圆的位置关系
考点三 切线的性质与判定
证圆的切线的技巧:(1)有公共点,连半径,证垂直;(2)无公共点,作垂直,证半径.
考点四 切线长与切线长定理
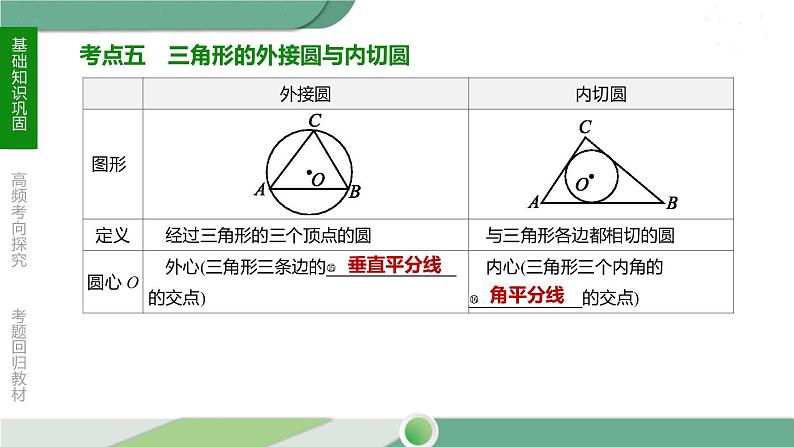
考点五 三角形的外接圆与内切圆
1.已知☉O的半径是5,直线l是☉O的切线,则点O到直线l的距离是( )A.2.5B.3C.5D.10
[解析]如果☉O的半径为r,圆心O到直线l的距离为d,那么直线l和☉O相切⇔d=r,所以点O到直线l的距离等于5.
2.[2019·苏州]如图24-1,AB为☉O的切线.切点为A,连接AO,BO,BO与☉O交于点C,延长BO与☉O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为( )A.54°B.36°C.32°D.27°
3.[2019·益阳]如图24-2,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )A.PA=PBB.∠BPD=∠APDC.AB⊥PDD.AB平分PD
[解析]∵PA,PB是☉O的切线,∴PA=PB,∴选项A成立;∴∠BPD=∠APD,∴选项B成立;∵PA,PB是☉O的切线,∴AB⊥PD,∴选项C成立;只有当AD∥PB,BD∥PA时,AB平分PD,∴选项D不一定成立.故选D.
4.如图24-3,AT切☉O于点A,AB是☉O的直径,若∠ABT=40°,则∠ATB= .
[解析]∵AT是☉O的切线,∴∠TAB=90°.∵∠ABT=40°,∴∠ATB=50°.
6.已知直角三角形的两直角边长分别为5和12,则它的外接圆半径R= ,内切圆半径r= .
7.若点O是等腰三角形ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为 .
8.如图24-5,已知AB是☉O的直径,BC是☉O的切线,切点为B,OC平行于弦AD.求证:DC是☉O的切线.
【失分点】定义法判定直线和圆的位置关系和d,r比较法判定直线和圆的位置关系相互混淆;切线长定理掌握得一知半解,导致做题过程复杂.
9.如图24-6,已知☉O的半径为5,直线EF经过☉O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与☉O相切的是( )A.OP=5B.OE=OFC.O到直线EF的距离是4D.OP⊥EF
10.点P是圆O外一点,过点P作圆O的切线,切点分别为A和B,写出由切线长定理能够直接得到的结论: .
AP=BP,∠APO=∠BPO
精练1 如图24-8,在☉O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )A.40°B.50°C.80°D.100°
[解析]因为CD为☉O的切线,所以∠OCD=90°.又因为∠BCD=50°,所以∠BCO=40°.因为OB=OC,所以∠BCO=∠OBC=40°.所以∠AOC=∠BCO+∠OBC=80°.
精练2[2019·贺州]如图24-9,BD是☉O的直径,弦BC与OA相交于点E,AF与☉O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.(1)求∠ADB的度数;(2)求AC的长度.
精练2[2019·贺州]如图24-9,BD是☉O的直径,弦BC与OA相交于点E,AF与☉O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.(2)求AC的长度.
例2 如图24-10,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且与BC边交于点E,D为直径BE所对的下半圆弧的中点,连接AD,交BC于点F,AC=FC.(1)求证:AC是☉O的切线;(2)已知半径R=5,EF=3,求DF的长.
解:(1)证明:连接OA,OD,如图所示.∵D为直径BE所对的下半圆弧的中点,∴OD⊥BE.∴∠D+∠DFO=90°.∵AC=FC,∴∠CAF=∠CFA.∵∠CFA=∠DFO,∴∠CAF=∠DFO.∵OA=OD,∴∠OAD=∠ODF.∴∠OAD+∠CAF=∠ODF+∠OFD=90°,即∠OAC=90°.∴OA⊥AC.∴AC是☉O的切线.
例2 如图24-10,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且与BC边交于点E,D为直径BE所对的下半圆弧的中点,连接AD,交BC于点F,AC=FC.(2)已知半径R=5,EF=3,求DF的长.
解:(1)证明:作OG⊥AB于点G.∵∠OCA=∠OGA,∠GAO=∠CAO,AO=AO,∴△OGA≌△OCA.∴OG=OC.∴AB是☉O的切线.
【方法点析】(1)判别直线是圆的切线有两种方法:若直线与圆有交点,则连接交点与圆心,证这条线段垂直于直线即可;若直线与圆没有直接的联系,则过圆心作直线的垂线段,证垂线段等于圆的半径即可.(2)求线段的长度有以下几种常用的方法:①用勾股定理,适用于已知两边的直角三角形中;②用相似三角形,适用于有相似三角形的图形中;③解直角三角形,适用于有锐角三角函数的图形中.
精练[2019·柳州十二中模拟]已知,AB是☉O的直径,点C在☉O上,点P是AB延长线上一点,连接CP.(1)如图24-12①,若∠PCB=∠A.①求证:直线PC是☉O的切线;②若CP=CA,OA=2,求CP的长;(2)如图②,若点M是弧AB的中点,CM交AB于点N,MN·MC=9,求BM的值.
精练[2019·柳州十二中模拟]已知,AB是☉O的直径,点C在☉O上,点P是AB延长线上一点,连接CP.(2)如图②,若点M是弧AB的中点,CM交AB于点N,MN·MC=9,求BM的值.
考向三 三角形的外接圆与内切圆
例4 (1)边长为1的正三角形的内切圆半径为 . (2)如图24-13所示,△ABC的三个顶点的坐标分别为A(4,3),B(-2,1),C(0,-1),则△ABC外接圆的圆心坐标是 ;△ABC外接圆的半径为 .
例4 (2)如图24-13所示,△ABC的三个顶点的坐标分别为A(4,3),B(-2,1),C(0,-1),则△ABC外接圆的圆心坐标是 ;△ABC外接圆的半径为 .
精练1 如图24-14,△ABC的内切圆☉O与AB,BC,CA分别相切于点D,E,F,且AD=2,△ABC的周长为14,则BC的长为( )A.3B.4C.5D.6
[解析]∵☉O与AB,BC,CA分别相切于点D,E,F,∴AF=AD=2,BD=BE,CE=CF.∵△ABC的周长为14,∴AD+AF+BE+BD+CE+CF=14,∴2(BE+CE)=10,∴BC=5.故选C.
精练2 如图24-15,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.则△ABC的内切圆☉O的半径r= .
精练3 已知一个三角形的三边长分别为5,7,8则其内切圆的半径为 .
教材母题——人教版九上P101T4如图24-16,直线AB经过☉O上的点C,并且OA=OB,CA=CB.求证:直线AB是☉O的切线.
与切线有关的辅助线的添加
证明:连接OC.∵OA=OB,CA=CB,∴△OAB是等腰三角形,OC是底边AB上的中线.∴OC⊥AB.∴直线AB是☉O的切线.
解:(1)证明:连接AD.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,∵AD=BD,∴∠BAD=∠B=30°,∴∠ADC=60°,∴∠DAC=180°-60°-30°=90°,∴AC是☉D的切线.
课时24 与圆有关的位置关系
点与圆的位置关系 直线与圆的位置关系 切线的判定和性质 三角形(多边形)的内切圆
考点一 点与圆的位置关系
考点二 直线与圆的位置关系
考点三 切线的性质与判定
证圆的切线的技巧:(1)有公共点,连半径,证垂直;(2)无公共点,作垂直,证半径.
考点四 切线长与切线长定理
考点五 三角形的外接圆与内切圆
1.已知☉O的半径是5,直线l是☉O的切线,则点O到直线l的距离是( )A.2.5B.3C.5D.10
[解析]如果☉O的半径为r,圆心O到直线l的距离为d,那么直线l和☉O相切⇔d=r,所以点O到直线l的距离等于5.
2.[2019·苏州]如图24-1,AB为☉O的切线.切点为A,连接AO,BO,BO与☉O交于点C,延长BO与☉O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为( )A.54°B.36°C.32°D.27°
3.[2019·益阳]如图24-2,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )A.PA=PBB.∠BPD=∠APDC.AB⊥PDD.AB平分PD
[解析]∵PA,PB是☉O的切线,∴PA=PB,∴选项A成立;∴∠BPD=∠APD,∴选项B成立;∵PA,PB是☉O的切线,∴AB⊥PD,∴选项C成立;只有当AD∥PB,BD∥PA时,AB平分PD,∴选项D不一定成立.故选D.
4.如图24-3,AT切☉O于点A,AB是☉O的直径,若∠ABT=40°,则∠ATB= .
[解析]∵AT是☉O的切线,∴∠TAB=90°.∵∠ABT=40°,∴∠ATB=50°.
6.已知直角三角形的两直角边长分别为5和12,则它的外接圆半径R= ,内切圆半径r= .
7.若点O是等腰三角形ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为 .
8.如图24-5,已知AB是☉O的直径,BC是☉O的切线,切点为B,OC平行于弦AD.求证:DC是☉O的切线.
【失分点】定义法判定直线和圆的位置关系和d,r比较法判定直线和圆的位置关系相互混淆;切线长定理掌握得一知半解,导致做题过程复杂.
9.如图24-6,已知☉O的半径为5,直线EF经过☉O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与☉O相切的是( )A.OP=5B.OE=OFC.O到直线EF的距离是4D.OP⊥EF
10.点P是圆O外一点,过点P作圆O的切线,切点分别为A和B,写出由切线长定理能够直接得到的结论: .
AP=BP,∠APO=∠BPO
精练1 如图24-8,在☉O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )A.40°B.50°C.80°D.100°
[解析]因为CD为☉O的切线,所以∠OCD=90°.又因为∠BCD=50°,所以∠BCO=40°.因为OB=OC,所以∠BCO=∠OBC=40°.所以∠AOC=∠BCO+∠OBC=80°.
精练2[2019·贺州]如图24-9,BD是☉O的直径,弦BC与OA相交于点E,AF与☉O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.(1)求∠ADB的度数;(2)求AC的长度.
精练2[2019·贺州]如图24-9,BD是☉O的直径,弦BC与OA相交于点E,AF与☉O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.(2)求AC的长度.
例2 如图24-10,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且与BC边交于点E,D为直径BE所对的下半圆弧的中点,连接AD,交BC于点F,AC=FC.(1)求证:AC是☉O的切线;(2)已知半径R=5,EF=3,求DF的长.
解:(1)证明:连接OA,OD,如图所示.∵D为直径BE所对的下半圆弧的中点,∴OD⊥BE.∴∠D+∠DFO=90°.∵AC=FC,∴∠CAF=∠CFA.∵∠CFA=∠DFO,∴∠CAF=∠DFO.∵OA=OD,∴∠OAD=∠ODF.∴∠OAD+∠CAF=∠ODF+∠OFD=90°,即∠OAC=90°.∴OA⊥AC.∴AC是☉O的切线.
例2 如图24-10,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且与BC边交于点E,D为直径BE所对的下半圆弧的中点,连接AD,交BC于点F,AC=FC.(2)已知半径R=5,EF=3,求DF的长.
解:(1)证明:作OG⊥AB于点G.∵∠OCA=∠OGA,∠GAO=∠CAO,AO=AO,∴△OGA≌△OCA.∴OG=OC.∴AB是☉O的切线.
【方法点析】(1)判别直线是圆的切线有两种方法:若直线与圆有交点,则连接交点与圆心,证这条线段垂直于直线即可;若直线与圆没有直接的联系,则过圆心作直线的垂线段,证垂线段等于圆的半径即可.(2)求线段的长度有以下几种常用的方法:①用勾股定理,适用于已知两边的直角三角形中;②用相似三角形,适用于有相似三角形的图形中;③解直角三角形,适用于有锐角三角函数的图形中.
精练[2019·柳州十二中模拟]已知,AB是☉O的直径,点C在☉O上,点P是AB延长线上一点,连接CP.(1)如图24-12①,若∠PCB=∠A.①求证:直线PC是☉O的切线;②若CP=CA,OA=2,求CP的长;(2)如图②,若点M是弧AB的中点,CM交AB于点N,MN·MC=9,求BM的值.
精练[2019·柳州十二中模拟]已知,AB是☉O的直径,点C在☉O上,点P是AB延长线上一点,连接CP.(2)如图②,若点M是弧AB的中点,CM交AB于点N,MN·MC=9,求BM的值.
考向三 三角形的外接圆与内切圆
例4 (1)边长为1的正三角形的内切圆半径为 . (2)如图24-13所示,△ABC的三个顶点的坐标分别为A(4,3),B(-2,1),C(0,-1),则△ABC外接圆的圆心坐标是 ;△ABC外接圆的半径为 .
例4 (2)如图24-13所示,△ABC的三个顶点的坐标分别为A(4,3),B(-2,1),C(0,-1),则△ABC外接圆的圆心坐标是 ;△ABC外接圆的半径为 .
精练1 如图24-14,△ABC的内切圆☉O与AB,BC,CA分别相切于点D,E,F,且AD=2,△ABC的周长为14,则BC的长为( )A.3B.4C.5D.6
[解析]∵☉O与AB,BC,CA分别相切于点D,E,F,∴AF=AD=2,BD=BE,CE=CF.∵△ABC的周长为14,∴AD+AF+BE+BD+CE+CF=14,∴2(BE+CE)=10,∴BC=5.故选C.
精练2 如图24-15,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.则△ABC的内切圆☉O的半径r= .
精练3 已知一个三角形的三边长分别为5,7,8则其内切圆的半径为 .
教材母题——人教版九上P101T4如图24-16,直线AB经过☉O上的点C,并且OA=OB,CA=CB.求证:直线AB是☉O的切线.
与切线有关的辅助线的添加
证明:连接OC.∵OA=OB,CA=CB,∴△OAB是等腰三角形,OC是底边AB上的中线.∴OC⊥AB.∴直线AB是☉O的切线.
解:(1)证明:连接AD.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,∵AD=BD,∴∠BAD=∠B=30°,∴∠ADC=60°,∴∠DAC=180°-60°-30°=90°,∴AC是☉D的切线.












