人教版中考数学第一轮考点过关：第三单元函数课时12一次函数及其应用

这是一份人教版中考数学第一轮考点过关：第三单元函数课时12一次函数及其应用，共59页。

课时12　一次函数及其应用
一次函数的概念　一次函数的图象和性质　一次函数解析式的确定　一次函数的应用
考点一　一次函数的概念
1.一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.2.一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
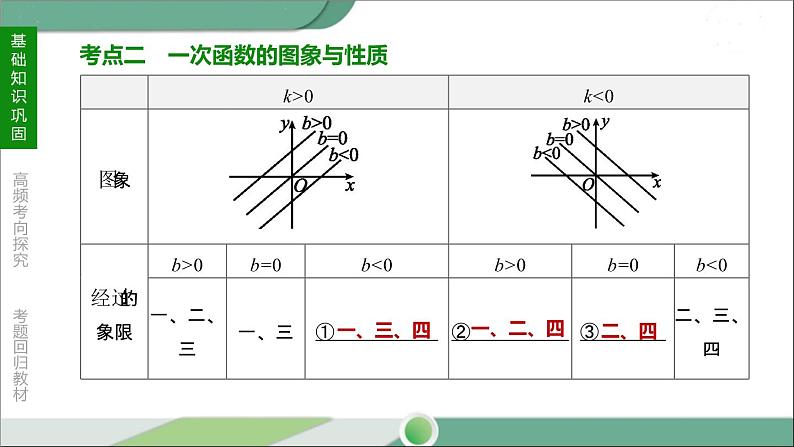
考点二　一次函数的图象与性质
考点三　一次函数的解析式的确定
1.方法:待定系数法2.步骤:(1)设:设一般式y=kx+b(k≠0);(2)列:找出直线上两点的坐标,分别代入y=kx+b,得到关于k,b的方程组;(3)解:解方程组,求得k,b的值;(4)依据k,b的值,写出一次函数的解析式.
考点四　一次函数与一次方程(组)、一元一次不等式的关系
1.一次函数与一次方程(组)的关系(1)一次函数的解析式本身就是一个二元一次方程;(2)方程kx+b=0的解⇔函数y=kx+b(k≠0)的图象与⑧　　　　轴交点的横坐标⇔函数y=kx+b(k≠0)中,y=⑨　　　时x的值; 
2.一次函数与一元一次不等式的关系(1)不等式kx+b>0(kx+b<0)的解集⇔函数y=kx+b(k≠0)的图象在x轴上方(下方)的部分对应的x的取值范围⇔函数y=kx+b(k≠0)中,y⑩　　0(y⑪　　0)时x的取值; (2)如图12-1,不等式k1x+b1>k2x+b2的解集是x>m;不等式k1x+b1≤k2x+b2的解集是⑫　　　. 
考点五　一次函数的应用
1.建立函数模型解决实际问题的步骤:(1)审题,明确变量x和y;(2)根据等量关系,建立函数解析式;(3)确定x的取值范围;(4)在x的取值范围内解决实际问题.
【温馨提示】说明函数是一次函数的情况:(1)当函数图象是直线(或线段、射线)时;(2)用表格呈现数据时:当自变量的变化值均匀时,函数值的变化也是均匀的,而且当自变量的变化值为1时,函数值的变化值就是自变量的系数k;(3)用语言呈现数据时:当一个量每变化一个单位时,另一量就相应地变化n个单位.
2.利用一次函数的图象解决实际问题的一般步骤:(1)观察图象,获取有效信息;(2)对获取的信息进行加工、处理,理清各数量之间的关系;(3)选择适当的数学工具(如函数、方程、不等式等),通过建模解决问题.
【温馨提示】要理解以下四点:①函数图象中的横、纵坐标代表的量;②拐点:图象上的拐点,既是前一段函数图象的终点,又是后一段函数图象的起 点;③水平线:函数值随自变量的变化而保持不变;④交点:表示两个函数的自变量与函数值分别对应相等,这个交点是函数值大小关系的“分界点”.
2.若点(3,1)在一次函数y=kx-2(k≠0)的图象上,则k的值是(　　)A.5B.4C.3D.1
[解析]∵点(3,1)在一次函数y=kx-2 (k≠0)的图象上,∴3k-2=1.解得k=1.故选D.
4.[八下P93练习第1题]直线y=2x-3与x轴交点坐标为　　　　,与y轴交点坐标为　　　　,图象经过　 　　　象限,y随x的增大而　　　. 5.[八下P99习题19.2第9题改编]点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.(1)用含x的式子表示S为　　 　　,x的取值范围为　　　　; (2)当点P的横坐标为5时,△OPA的面积为　　　　; (3)△OPA的面积　　　　24(填“<”或“≥”). 
6.[八下P109复习题19第13题改编]一个有进水管与出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图12-3所示.(1)当0≤x≤4时,y关于x的函数解析式是　　　　; (2)当4【失分点】忽视函数定义中的限制条件;忽略坐标系中表示线段的长时要取点的坐标的绝对值;分类讨论不全.
8.已知一次函数y=kx+b,且当-3≤x≤1时,1≤y≤9,则k+b的值为　　　　. 
例1 已知一次函数y=2x+b,其中b<0,与解析式描述相符的函数图象可能是图12-4中的(　　)
考向一　一次函数的图象和性质
[解析]根据题目的条件逐一排查,可得答案.本题中k=2>0,一次函数的图象从左到右是向上的趋势,故可排除B,D.因为b<0,所以一次函数的图象与y轴的负半轴相交.故选A.
【方法点析】直线y=kx+b所在的位置与k,b的符号关系:k>0时,直线经过第一、三象限;k<0时,直线经过第二、四象限.b>0时,直线与y轴的正半轴相交;b=0 时,直线过原点;b<0时,直线与y轴的负半轴相交.
精练1 如图12-5,直线y=2x必过的点是 (　　)A.(2,1)B.(2,2)C.(-1,-1)D.(0,0)
精练2 对于函数y=2x-1,下列说法正确的是(　　)A.它的图象过点(1,0)B.y值随着x值增大而减小C.它的图象经过第二象限D.当x>1时,y>0
考向二　一次函数解析式的求解
解:(1)∵图象平行于直线y=2x-1,∴k=2,设函数解析式为y=2x+b,将(1,3)代入得3=2×1+b.∴b=1.∴y=2x+1.
精练 如图12-6,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a).(1)求直线l1的解析式;(2)求四边形PAOC的面积.
精练 如图12-6,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a).(2)求四边形PAOC的面积.
考向三　一次函数图象的平移
解:(1)点(0,1)向下平移2个单位后的坐标是(0,-1).直线y=2x+1向下平移2个单位后所得图象的解析式是y=2x-1.
解:(2)直线y=2x+1向右平移2个单位后所得图象的解析式是y=2x-3.
【方法点析】直线y=kx+b(k≠0)在平移过程中k值不变.平移的规律是:若上下平移,则直接在常数b后加上或减去平移的单位长度数;若向左或向右平移m个单位长度,则直线y=kx+b(k≠0)变为y=k(x±m)+b.其口诀是上加下减,左加右减.
精练2 [2019·邵阳]一次函数y1=k1x+b1的图象l1如图12-8所示,将直线l1向下平移若干个单位后得直线l2, l2的函数表达式为y2=k2x+b2.下列说法中错误的是(　　)A.k1=k2B.b1b2D.当x=5时,y1>y2
[解析]∵将直线l1向下平移若干个单位后得直线l2,∴直线l1∥直线l2, ∴k1=k2,∴b1>b2.当x=5时,y1>y2.故选B.
考向四　一次函数的应用
精练1 [2019·东城一模]弹簧原长(不挂重物)15 cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:当重物质量为5 kg(在弹性限度内)时,弹簧总长L(cm)是(　　)A.22.5D.30
精练2 [2019·密云一模]某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图12-10所示,则下列判断错误的是(　　)A.每月上网不足25小时,选择A方式最省钱B.每月上网时间为30小时,选择B方式最省钱C.每月上网费用为60元,选择B方式比A方式时间长D.每月上网时间超过70小时,选择C方式最省钱
精练3 下表是世界人口增长趋势数据表:(1)请你认真研究上面数据表,求出从1960年到2010年世界人口平均每年增长多少亿人;(2)利用你在(1)中所得到的结论,以1960年30亿人口为基础,设计一个最能反映人口数量y关于年份x的函数关系式,并求出这个函数的解析式;(3)利用你在(2)中所得的函数解析式,预测2020年世界人口将达到多少亿人.
解:(1)从1960年到2010年世界人口平均每年增长(69-30)÷(2010-1960)=39÷50=0.78(亿).
精练3 [2016·柳州]下表是世界人口增长趋势数据表:(2)利用你在(1)中所得到的结论,以1960年30亿人口为基础,设计一个最能反映人口数量y关于年份x的函数关系式,并求出这个函数的解析式;
精练3 [2016·柳州]下表是世界人口增长趋势数据表:(3)利用你在(2)中所得的函数解析式,预测2020年世界人口将达到多少亿人.
考向五　一次函数与方程、不等式的关系
例5 如图12-11,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是(　　)A.x>-2B.x>0C.x>1D.x<1
精练 如图12-12,一次函数y=kx+b的图象与坐标轴的交点坐标分别为A(0,2), B(-3,0),下列说法:①y随x的增大而减小;②b=2;③关于x的方程kx+b=0的解为x=2;④关于x的不等式kx+b<0的解集为x<-3.其中说法正确的个数有(　　)A.1个B.2个C.3个D.4个
教材母题——人教版八下P108复习题19T10已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10.设△OPA的面积为S.(1)求S关于x的函数解析式;(2)求x的取值范围;(3)当S=12时,求P点坐标;(4)画出S与x的函数关系图象.
直线背景下的三角形面积问题
解:(1)∵x+y=10,∴y=10-x,∴S=8(10-x)÷2=40-4x.
解: (2)∵40-4x>0,∴x<10,∴0教材母题——人教版八下P108复习题19T10已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10.设△OPA的面积为S.(2)求x的取值范围;
解: (3)∵S=12,∴12=40-4x,解得x=7.∴y=10-7=3,∴S=12时,P点坐标为(7,3).
教材母题——人教版八下P108复习题19T10已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10.设△OPA的面积为S.(3)当S=12时,求P点坐标;
解: (4)如图所示.
教材母题——人教版八下P108复习题19T10已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10.设△OPA的面积为S.(4)画出S与x的函数关系图象.
【方法点析】根据直线解析式将问题由二元变一元,体现了化归转化的思想.
精练 如图12-13,已知A(-1,3),B(3,-1),过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,在直线AB上是否存在点P,使得S△PAC=S△PBD?若存在,求出点P的坐标;若不存在,请说明理由.