还剩38页未读，
继续阅读
所属成套资源：数学苏教版必修第二册全册课堂教学PPT
成套系列资料，整套一键下载
苏教版必修二 高中数学阶段提升课第五课立体几何初步课件PPT
展开
这是一份数学苏教版 (2019)本册综合优秀ppt课件，共46页。PPT课件主要包含了思维导图·构建网络，考点整合·素养提升等内容，欢迎下载使用。
题组训练一 空间中的平行关系 1.如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点.求证:(1)GE∥平面BDD1B1;(2)平面BDF∥平面B1D1H.
【证明】(1)取B1D1的中点O,连接GO,OB,易证OG? B1C1,BE? B1C1,所以OG?BE,四边形BEGO为平行四边形,所以OB∥GE.因为OB⊂平面BDD1B1,GE⊄平面BDD1B1,所以GE∥平面BDD1B1.
(2)由正方体性质得B1D1∥BD,因为B1D1⊄平面BDF,BD⊂平面BDF,所以B1D1∥平面BDF.连接HB,D1F,易证HBFD1是平行四边形得HD1∥BF.因为HD1⊄平面BDF,BF⊂平面BDF,所以HD1∥平面BDF.因为B1D1∩HD1=D1,所以平面BDF∥平面B1D1H.
【方法技巧】1.判断或证明线面平行的常用方法:(1)利用线面平行的定义(无公共点);(2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α);(3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);(4)利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).
2.证明面面平行的方法:(1)利用面面平行的定义;(2)利用面面平行的判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行;(3)垂直于同一条直线的两个平面平行;(4)两个平面同时平行于第三个平面,那么这两个平面平行;(5)利用“线线平行”“线面平行”“面面平行”的相互转化.
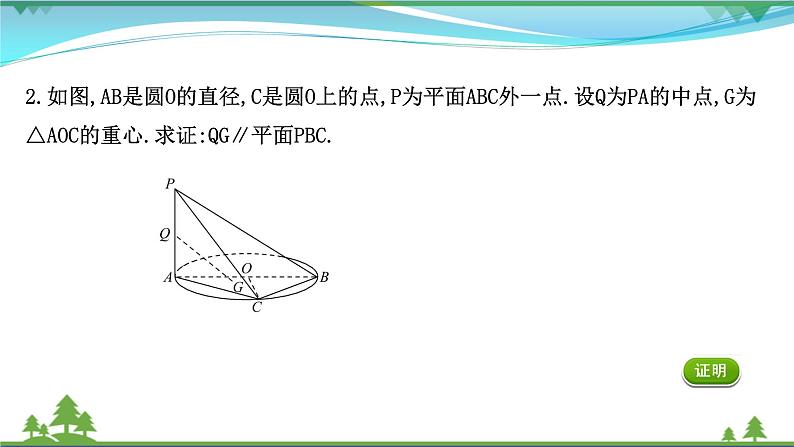
2.如图,AB是圆O的直径,C是圆O上的点,P为平面ABC外一点.设Q为PA的中点,G为△AOC的重心.求证:QG∥平面PBC.
【证明】如图,连接OG并延长,交AC于点M,连接QM,QO,由G为△AOC的重心,得M为AC的中点.由Q为PA的中点,得QM∥PC.又O为AB的中点,所以OM∥BC.因为QM∩MO=M,QM⊂平面QMO,MO⊂平面QMO,BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,所以平面QMO∥平面PBC.又QG⊂平面QMO,所以QG∥平面PBC.
题组训练二 空间中的垂直关系 1.如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.(1)求证:BC⊥AF;(2)试判断直线AF与平面EBC是否垂直.若垂直,请给出证明;若不垂直,请说明理由.
【解析】(1)因为EF∥AB,所以EF与AB确定平面EABF,因为EA⊥平面ABCD,所以EA⊥BC.由已知得AB⊥BC且EA∩AB=A,所以BC⊥平面EABF.又AF⊂平面EABF,所以BC⊥AF.
(2)直线AF垂直于平面EBC.证明如下:由(1)可知,AF⊥BC.在四边形EABF中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90°,所以tan∠EBA=tan∠FAE= ,则∠EBA=∠FAE.设AF∩BE=P,因为∠PAE+∠PAB=90°,故∠PBA+∠PAB=90°.则∠APB=90°,即EB⊥AF.又因为EB∩BC=B,所以AF⊥平面EBC.
2.如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.
【证明】(1)如图所示,取EC的中点F,连接DF,易知DF∥BC,因为EC⊥BC,所以DF⊥EC.在Rt△DEF和Rt△DBA中,因为EF= EC=BD,FD=BC=AB,所以Rt△DFE≌Rt△ABD,故DE=DA.
(2)取CA的中点N,连接MN,BN,则MN? EC,所以MN∥BD,即N点在平面BDM内.因为EC⊥平面ABC,所以EC⊥BN.又CA⊥BN,EC∩CA=C,所以BN⊥平面ECA.因为BN在平面MNBD内,所以平面MNBD⊥平面ECA,即平面BDM⊥平面ECA.
(3)因为DM∥BN,BN⊥平面ECA,所以DM⊥平面ECA.又DM⊂平面DEA,所以平面DEA⊥平面ECA.
【方法技巧】空间垂直关系的判定方法(1)判定线线垂直的方法①计算所成的角为90°(包括平面角和异面直线所成的角);②线面垂直的性质(若a⊥α,b⊂α,则a⊥b).
(2)判定线面垂直的方法①线面垂直的定义(一般不易验证任意性);②线面垂直的判定定理(a⊥m,a⊥n,m⊂α,n⊂α,m∩n=A⇒a⊥α);③平行线垂直平面的传递性质(a∥b,b⊥α⇒a⊥α);④面面垂直的性质定理(α⊥β,α∩β=l,a⊂β,a⊥l⇒a⊥α);⑤面面平行的性质(a⊥α,α∥β⇒a⊥β);⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ⇒l⊥γ).
(3)面面垂直的判定方法①根据定义(作两平面构成二面角的平面角,计算其为90°);②面面垂直的判定定理(a⊥β,a⊂α⇒α⊥β).
题组训练三 空间几何体的体积及表面积 1.已知三棱柱的底面是边长为4的正三角形,侧棱长为3,一条侧棱与相邻两边所成的角都是60°,求棱柱的侧面积.
【解析】如图,侧棱AA1与底边AB,AC所成的角为60°,过A1作A1O⊥底面ABC,连接AO,过A1作A1D⊥AB于D,连接OD,因为∠A1AB=∠A1AC=60°,所以AO为∠BAC的平分线,又因为△ABC为正三角形,所以AO⊥BC,又因为A1O⊥BC,A1O∩AO=O,所以BC⊥平面AA1O,所以BC⊥AA1,所以BC⊥BB1,
所以四边形BCC1B1为矩形,得S三棱柱侧=
2.已知在三棱锥A-BCD中,AB=CD=1,BC=BD=AC=AD=2.求三棱锥A-BCD的体积.
【解析】如图所示,取AB的中点M,连接CM,DM,则平面CDM把三棱锥分成两个小三棱锥.因为AC=BC,所以AB⊥CM.因为AD=BD,所以AB⊥DM.因为CM∩DM=M,所以AB⊥平面CDM.CM=DM= 取CD的中点N,连接MN,则MN⊥CD.所以MN=
从而S△CDM= 所以VA-BCD=VA-CDM+VB-CDM= S△CDM·AM+ S△CDM·BM= S△CDM·AB= × ×1= .
【方法技巧】 几何体的表面积及体积的计算是现实生活中经常遇到的问题,在计算中应注意各数量之间的关系及各元素之间的位置关系,特别是特殊的柱、锥、台体,要注意其中矩形、梯形及直角三角形等重要的平面图形的应用,注意分割与组合的合理应用,关注展开与折叠问题.
题组训练四 空间角的计算问题 1.如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,AB≠AC,D,E分别是BC,AB的中点,AC>AD,设PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是________.
【解析】因为D,E分别是BC,AB的中点,所以DE∥AC,所以PC与DE所成的角为∠PCA,即α;连接AD,因为PA⊥平面ABC,所以PD与平面ABC所成的角为∠PDA,即β;过A作AH⊥BC,垂足为H,连接PH,易证BC⊥平面PAH,所以∠PHA是二面角P-BC-A的平面角,即γ.因为AB≠AC,
所以AD>AH,又AC>AD,所以AC>AD>AH,所以 所以tan α
【解析】(1)因为A'C'∥AC,所以AO与A'C'所成的角就是∠OAC.因为AB⊥平面BC',OC⊂平面BC',所以OC⊥AB,又OC⊥BO,AB∩BO=B.所以OC⊥平面ABO.又OA⊂平面ABO,所以OC⊥OA.在Rt△AOC中,OC= ,AC= ,sin∠OAC= 所以∠OAC=30°,即AO与A'C'所成角的度数为30°.
(2)如图,作OE⊥BC于E,连接AE.因为平面BC'⊥平面ABCD,所以OE⊥平面ABCD,所以∠OAE为OA与平面ABCD所成的角.在Rt△OAE中,OE= AE= 所以tan∠OAE=
(3)因为OC⊥OA,OC⊥OB,OA∩OB=O,所以OC⊥平面AOB.又因为OC⊂平面AOC,所以平面AOB⊥平面AOC.即平面AOB与平面AOC所成角的度数为90°.
【方法技巧】空间角的求法 求空间各种角的大小一般都转化为平面角来计算,空间角的计算步骤:一作,二证,三计算.(1)求异面直线所成的角常用平移转化法(转化为相交直线的夹角).(2)求直线与平面所成的角常用射影转化法(作垂线、找射影).(3)二面角的平面角的作法常有三种:①定义法;②垂线法;③垂面法.
题组训练五 平面图形的翻折问题 1.如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC= AP,D是AP的中点,E,F分别为PD,PC的中点,将△PCD沿CD折起得到四棱锥P-ABCD.(1)G为线段BC上任一点,求证:平面EFG⊥平面PAD;(2)当G为BC的中点时,求证:AP∥平面EFG.
【证明】(1)在直角梯形ABCP中,因为BC∥AP,BC= AP,D为AP的中点.所以BC?AD,又AB⊥AP,AB=BC,所以四边形ABCD为正方形,所以CD⊥AP,CD⊥AD,CD⊥PD.在四棱锥P-ABCD中,因为E,F分别为PD,PC的中点,所以EF∥CD,EF⊥AD,EF⊥PD.又PD∩AD=D,PD⊂平面PAD,AD⊂平面PAD.
所以EF⊥平面PAD.又EF⊂平面EFG,所以平面EFG⊥平面PAD.(2)方法一:因为G,F分别为BC和PC的中点,所以GF∥BP.因为GF⊄平面PAB,BP⊂平面PAB,所以GF∥平面PAB.由(1)知,EF∥DC,因为AB∥DC,所以EF∥AB.
因为EF⊄平面PAB,AB⊂平面PAB,所以EF∥平面PAB.因为EF∩GF=F,EF⊂平面EFG,GF⊂平面EFG.所以平面EFG∥平面PAB.因为PA⊂平面PAB,所以PA∥平面EFG.
方法二:取AD中点H(作图略),连接GH,HE.由(1)知四边形ABCD为平行四边形.又G,H分别为BC,AD的中点,所以GH∥CD.由(1)知,EF∥CD,所以EF∥GH.所以E,F,G,H四点共面.因为E,H分别为PD,AD的中点,所以EH∥PA.因为PA⊄平面EFGH,EH⊂平面EFGH.所以PA∥平面EFGH,即PA∥平面EFG.
2.如图(1)所示,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF⊥平面ABCD,连接部分线段后围成一个空间几何体,如图(2)所示.(1)求证:BE∥平面ADF;(2)求三棱锥F-BCE的体积.
【解析】(1)方法一:取DF的中点G,连接AG,EG,因为CE= DF,所以EG?CD.又因为AB?CD,所以EG?AB,所以四边形ABEG为平行四边形,所以BE∥AG.因为BE⊄平面ADF,AG⊂平面ADF,所以BE∥平面ADF.
方法二:由题图(1)可知BC∥AD,CE∥DF,折叠之后平行关系不变. 因为BC⊄平面ADF,AD⊂平面ADF,所以BC∥平面ADF.同理CE∥平面ADF.因为BC∩CE=C,BC,CE⊂平面BCE,所以平面BCE∥平面ADF.因为BE⊂平面BCE,所以BE∥平面ADF.
(2)方法一:因为VF-BCE=VB-CEF,由题图(1)可知BC⊥CD.因为平面DCEF⊥平面ABCD,平面DCEF∩平面ABCD=CD,BC⊂平面ABCD,所以BC⊥平面DCEF.由题图(1)可知DC=CE=1,S△CEF= CE·DC= ,所以VF-BCE=VB-CEF= ×BC×S△CEF= .
方法二:由题图(1)可知,CD⊥BC,CD⊥CE,因为BC∩CE=C,所以CD⊥平面BCE.因为DF∥CE,点F到平面BCE的距离等于点D到平面BCE的距离,即为CD,由题图(1)可知,BC=CE=1,S△BCE= BC·CE= ,所以VF-BCE= ×CD×S△BCE= .
方法三:过E作EH⊥FC,垂足为H,如图所示,由题图(1)可知,BC⊥CD,因为平面DCEF⊥平面ABCD,平面DCEF∩平面ABCD=CD,BC⊂平面ABCD,所以BC⊥平面DCEF.因为FC,EH⊂平面DCEF,所以BC⊥EH,BC⊥FC,因为BC∩FC=C,所以EH⊥平面BCF.由FD⊥DC得,FC= S△BCF= BC·CF= ,在△CEF中,由等面积法可得EH= ,所以VF-BCE=VE-BCF= ×EH×S△BCF=
题组训练一 空间中的平行关系 1.如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点.求证:(1)GE∥平面BDD1B1;(2)平面BDF∥平面B1D1H.
【证明】(1)取B1D1的中点O,连接GO,OB,易证OG? B1C1,BE? B1C1,所以OG?BE,四边形BEGO为平行四边形,所以OB∥GE.因为OB⊂平面BDD1B1,GE⊄平面BDD1B1,所以GE∥平面BDD1B1.
(2)由正方体性质得B1D1∥BD,因为B1D1⊄平面BDF,BD⊂平面BDF,所以B1D1∥平面BDF.连接HB,D1F,易证HBFD1是平行四边形得HD1∥BF.因为HD1⊄平面BDF,BF⊂平面BDF,所以HD1∥平面BDF.因为B1D1∩HD1=D1,所以平面BDF∥平面B1D1H.
【方法技巧】1.判断或证明线面平行的常用方法:(1)利用线面平行的定义(无公共点);(2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α);(3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);(4)利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).
2.证明面面平行的方法:(1)利用面面平行的定义;(2)利用面面平行的判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行;(3)垂直于同一条直线的两个平面平行;(4)两个平面同时平行于第三个平面,那么这两个平面平行;(5)利用“线线平行”“线面平行”“面面平行”的相互转化.
2.如图,AB是圆O的直径,C是圆O上的点,P为平面ABC外一点.设Q为PA的中点,G为△AOC的重心.求证:QG∥平面PBC.
【证明】如图,连接OG并延长,交AC于点M,连接QM,QO,由G为△AOC的重心,得M为AC的中点.由Q为PA的中点,得QM∥PC.又O为AB的中点,所以OM∥BC.因为QM∩MO=M,QM⊂平面QMO,MO⊂平面QMO,BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,所以平面QMO∥平面PBC.又QG⊂平面QMO,所以QG∥平面PBC.
题组训练二 空间中的垂直关系 1.如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.(1)求证:BC⊥AF;(2)试判断直线AF与平面EBC是否垂直.若垂直,请给出证明;若不垂直,请说明理由.
【解析】(1)因为EF∥AB,所以EF与AB确定平面EABF,因为EA⊥平面ABCD,所以EA⊥BC.由已知得AB⊥BC且EA∩AB=A,所以BC⊥平面EABF.又AF⊂平面EABF,所以BC⊥AF.
(2)直线AF垂直于平面EBC.证明如下:由(1)可知,AF⊥BC.在四边形EABF中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90°,所以tan∠EBA=tan∠FAE= ,则∠EBA=∠FAE.设AF∩BE=P,因为∠PAE+∠PAB=90°,故∠PBA+∠PAB=90°.则∠APB=90°,即EB⊥AF.又因为EB∩BC=B,所以AF⊥平面EBC.
2.如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.
【证明】(1)如图所示,取EC的中点F,连接DF,易知DF∥BC,因为EC⊥BC,所以DF⊥EC.在Rt△DEF和Rt△DBA中,因为EF= EC=BD,FD=BC=AB,所以Rt△DFE≌Rt△ABD,故DE=DA.
(2)取CA的中点N,连接MN,BN,则MN? EC,所以MN∥BD,即N点在平面BDM内.因为EC⊥平面ABC,所以EC⊥BN.又CA⊥BN,EC∩CA=C,所以BN⊥平面ECA.因为BN在平面MNBD内,所以平面MNBD⊥平面ECA,即平面BDM⊥平面ECA.
(3)因为DM∥BN,BN⊥平面ECA,所以DM⊥平面ECA.又DM⊂平面DEA,所以平面DEA⊥平面ECA.
【方法技巧】空间垂直关系的判定方法(1)判定线线垂直的方法①计算所成的角为90°(包括平面角和异面直线所成的角);②线面垂直的性质(若a⊥α,b⊂α,则a⊥b).
(2)判定线面垂直的方法①线面垂直的定义(一般不易验证任意性);②线面垂直的判定定理(a⊥m,a⊥n,m⊂α,n⊂α,m∩n=A⇒a⊥α);③平行线垂直平面的传递性质(a∥b,b⊥α⇒a⊥α);④面面垂直的性质定理(α⊥β,α∩β=l,a⊂β,a⊥l⇒a⊥α);⑤面面平行的性质(a⊥α,α∥β⇒a⊥β);⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ⇒l⊥γ).
(3)面面垂直的判定方法①根据定义(作两平面构成二面角的平面角,计算其为90°);②面面垂直的判定定理(a⊥β,a⊂α⇒α⊥β).
题组训练三 空间几何体的体积及表面积 1.已知三棱柱的底面是边长为4的正三角形,侧棱长为3,一条侧棱与相邻两边所成的角都是60°,求棱柱的侧面积.
【解析】如图,侧棱AA1与底边AB,AC所成的角为60°,过A1作A1O⊥底面ABC,连接AO,过A1作A1D⊥AB于D,连接OD,因为∠A1AB=∠A1AC=60°,所以AO为∠BAC的平分线,又因为△ABC为正三角形,所以AO⊥BC,又因为A1O⊥BC,A1O∩AO=O,所以BC⊥平面AA1O,所以BC⊥AA1,所以BC⊥BB1,
所以四边形BCC1B1为矩形,得S三棱柱侧=
2.已知在三棱锥A-BCD中,AB=CD=1,BC=BD=AC=AD=2.求三棱锥A-BCD的体积.
【解析】如图所示,取AB的中点M,连接CM,DM,则平面CDM把三棱锥分成两个小三棱锥.因为AC=BC,所以AB⊥CM.因为AD=BD,所以AB⊥DM.因为CM∩DM=M,所以AB⊥平面CDM.CM=DM= 取CD的中点N,连接MN,则MN⊥CD.所以MN=
从而S△CDM= 所以VA-BCD=VA-CDM+VB-CDM= S△CDM·AM+ S△CDM·BM= S△CDM·AB= × ×1= .
【方法技巧】 几何体的表面积及体积的计算是现实生活中经常遇到的问题,在计算中应注意各数量之间的关系及各元素之间的位置关系,特别是特殊的柱、锥、台体,要注意其中矩形、梯形及直角三角形等重要的平面图形的应用,注意分割与组合的合理应用,关注展开与折叠问题.
题组训练四 空间角的计算问题 1.如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,AB≠AC,D,E分别是BC,AB的中点,AC>AD,设PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是________.
【解析】因为D,E分别是BC,AB的中点,所以DE∥AC,所以PC与DE所成的角为∠PCA,即α;连接AD,因为PA⊥平面ABC,所以PD与平面ABC所成的角为∠PDA,即β;过A作AH⊥BC,垂足为H,连接PH,易证BC⊥平面PAH,所以∠PHA是二面角P-BC-A的平面角,即γ.因为AB≠AC,
所以AD>AH,又AC>AD,所以AC>AD>AH,所以 所以tan α
【解析】(1)因为A'C'∥AC,所以AO与A'C'所成的角就是∠OAC.因为AB⊥平面BC',OC⊂平面BC',所以OC⊥AB,又OC⊥BO,AB∩BO=B.所以OC⊥平面ABO.又OA⊂平面ABO,所以OC⊥OA.在Rt△AOC中,OC= ,AC= ,sin∠OAC= 所以∠OAC=30°,即AO与A'C'所成角的度数为30°.
(2)如图,作OE⊥BC于E,连接AE.因为平面BC'⊥平面ABCD,所以OE⊥平面ABCD,所以∠OAE为OA与平面ABCD所成的角.在Rt△OAE中,OE= AE= 所以tan∠OAE=
(3)因为OC⊥OA,OC⊥OB,OA∩OB=O,所以OC⊥平面AOB.又因为OC⊂平面AOC,所以平面AOB⊥平面AOC.即平面AOB与平面AOC所成角的度数为90°.
【方法技巧】空间角的求法 求空间各种角的大小一般都转化为平面角来计算,空间角的计算步骤:一作,二证,三计算.(1)求异面直线所成的角常用平移转化法(转化为相交直线的夹角).(2)求直线与平面所成的角常用射影转化法(作垂线、找射影).(3)二面角的平面角的作法常有三种:①定义法;②垂线法;③垂面法.
题组训练五 平面图形的翻折问题 1.如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC= AP,D是AP的中点,E,F分别为PD,PC的中点,将△PCD沿CD折起得到四棱锥P-ABCD.(1)G为线段BC上任一点,求证:平面EFG⊥平面PAD;(2)当G为BC的中点时,求证:AP∥平面EFG.
【证明】(1)在直角梯形ABCP中,因为BC∥AP,BC= AP,D为AP的中点.所以BC?AD,又AB⊥AP,AB=BC,所以四边形ABCD为正方形,所以CD⊥AP,CD⊥AD,CD⊥PD.在四棱锥P-ABCD中,因为E,F分别为PD,PC的中点,所以EF∥CD,EF⊥AD,EF⊥PD.又PD∩AD=D,PD⊂平面PAD,AD⊂平面PAD.
所以EF⊥平面PAD.又EF⊂平面EFG,所以平面EFG⊥平面PAD.(2)方法一:因为G,F分别为BC和PC的中点,所以GF∥BP.因为GF⊄平面PAB,BP⊂平面PAB,所以GF∥平面PAB.由(1)知,EF∥DC,因为AB∥DC,所以EF∥AB.
因为EF⊄平面PAB,AB⊂平面PAB,所以EF∥平面PAB.因为EF∩GF=F,EF⊂平面EFG,GF⊂平面EFG.所以平面EFG∥平面PAB.因为PA⊂平面PAB,所以PA∥平面EFG.
方法二:取AD中点H(作图略),连接GH,HE.由(1)知四边形ABCD为平行四边形.又G,H分别为BC,AD的中点,所以GH∥CD.由(1)知,EF∥CD,所以EF∥GH.所以E,F,G,H四点共面.因为E,H分别为PD,AD的中点,所以EH∥PA.因为PA⊄平面EFGH,EH⊂平面EFGH.所以PA∥平面EFGH,即PA∥平面EFG.
2.如图(1)所示,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF⊥平面ABCD,连接部分线段后围成一个空间几何体,如图(2)所示.(1)求证:BE∥平面ADF;(2)求三棱锥F-BCE的体积.
【解析】(1)方法一:取DF的中点G,连接AG,EG,因为CE= DF,所以EG?CD.又因为AB?CD,所以EG?AB,所以四边形ABEG为平行四边形,所以BE∥AG.因为BE⊄平面ADF,AG⊂平面ADF,所以BE∥平面ADF.
方法二:由题图(1)可知BC∥AD,CE∥DF,折叠之后平行关系不变. 因为BC⊄平面ADF,AD⊂平面ADF,所以BC∥平面ADF.同理CE∥平面ADF.因为BC∩CE=C,BC,CE⊂平面BCE,所以平面BCE∥平面ADF.因为BE⊂平面BCE,所以BE∥平面ADF.
(2)方法一:因为VF-BCE=VB-CEF,由题图(1)可知BC⊥CD.因为平面DCEF⊥平面ABCD,平面DCEF∩平面ABCD=CD,BC⊂平面ABCD,所以BC⊥平面DCEF.由题图(1)可知DC=CE=1,S△CEF= CE·DC= ,所以VF-BCE=VB-CEF= ×BC×S△CEF= .
方法二:由题图(1)可知,CD⊥BC,CD⊥CE,因为BC∩CE=C,所以CD⊥平面BCE.因为DF∥CE,点F到平面BCE的距离等于点D到平面BCE的距离,即为CD,由题图(1)可知,BC=CE=1,S△BCE= BC·CE= ,所以VF-BCE= ×CD×S△BCE= .
方法三:过E作EH⊥FC,垂足为H,如图所示,由题图(1)可知,BC⊥CD,因为平面DCEF⊥平面ABCD,平面DCEF∩平面ABCD=CD,BC⊂平面ABCD,所以BC⊥平面DCEF.因为FC,EH⊂平面DCEF,所以BC⊥EH,BC⊥FC,因为BC∩FC=C,所以EH⊥平面BCF.由FD⊥DC得,FC= S△BCF= BC·CF= ,在△CEF中,由等面积法可得EH= ,所以VF-BCE=VE-BCF= ×EH×S△BCF=
相关课件
数学必修2第一章 立体几何初步综合与测试复习课件ppt： 这是一份数学必修2第一章 立体几何初步综合与测试复习课件ppt，共31页。
苏教版必修二 高中数学阶段提升课第一课平面向量课件PPT： 这是一份高中苏教版 (2019)本册综合评优课ppt课件，共31页。PPT课件主要包含了思维导图·构建网络，考点整合·素养提升，解析答案等内容，欢迎下载使用。
苏教版必修二 高中数学阶段提升课第三课解三角形课件PPT： 这是一份高中数学苏教版 (2019)必修 第二册本册综合优秀课件ppt，共29页。PPT课件主要包含了思维导图·构建网络，考点整合·素养提升等内容，欢迎下载使用。
