初中数学18.1.2 平行四边形的判定优质ppt课件

这是一份初中数学18.1.2 平行四边形的判定优质ppt课件，共21页。PPT课件主要包含了情境引入，连结AC，ABCD已知，BCDA已知，∴AD∥BC，同理得AB∥CD，OAOC已知，OBOD已知，平行四边形判定定理，ADBC等内容，欢迎下载使用。

1.平行四边形判定方法的探究.（重点）2.平行四边形判定方法的理解和灵活应用.（难点）
学习了平行四边形之后，小明回家用细木棒钉制了一个平行四边形.第二天，小明拿着自己动手做的平行四边形向同学们展示. 小辉却问：你凭什么确定这四边形就是平行四边形呢? 大家都困惑了……
小强提议说：我们可以度量它的边，如果它的两组对边分别相等，那么它就是一个平行四边形.
你能根据平行四边形的定义证明它们吗？
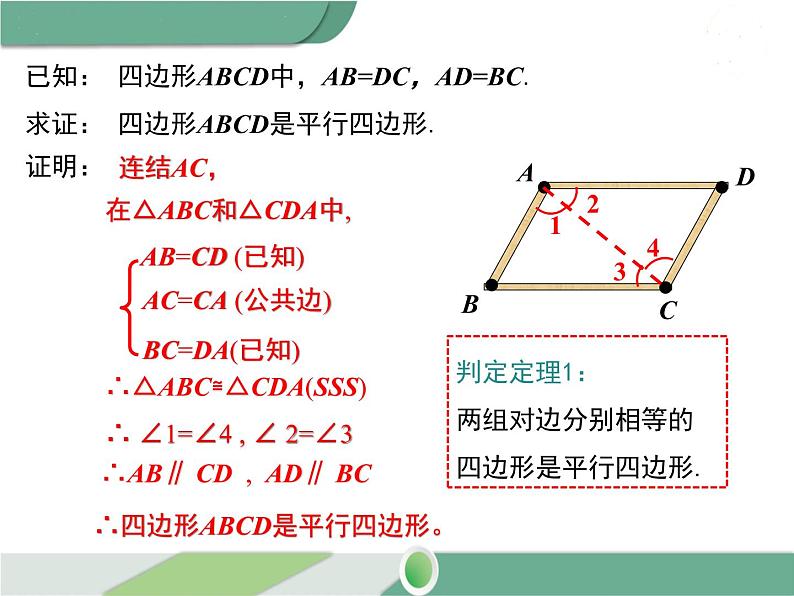
已知： 四边形ABCD中，AB=DC，AD=BC.求证： 四边形ABCD是平行四边形.
在△ABC和△CDA中,
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
判定定理1：两组对边分别相等的四边形是平行四边形.
小伟提议说：我们可以度量它的角，如果它的两组对角分别相等，那么它就是一个平行四边形.
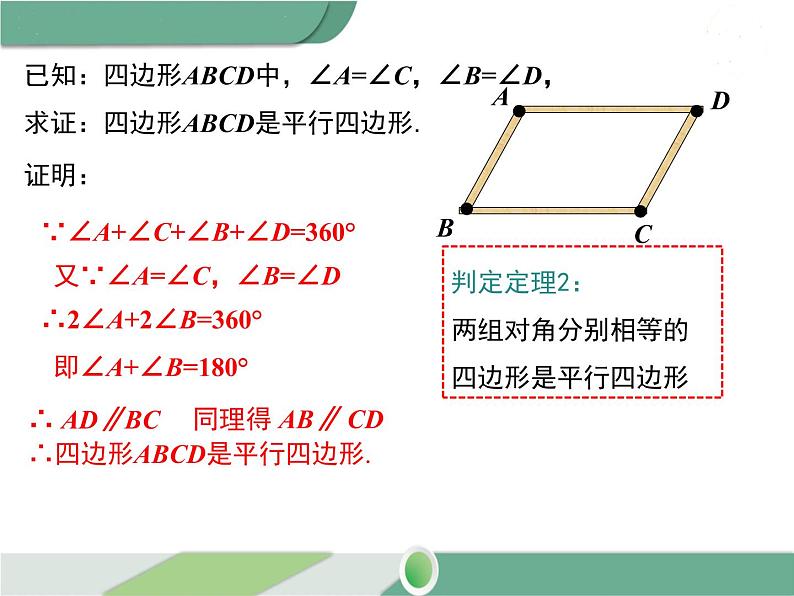
已知：四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形.
又∵∠A=∠C，∠B=∠D
∵∠A+∠C+∠B+∠D=360°
∴2∠A+2∠B=360°
即∠A+∠B=180°
∴四边形ABCD是平行四边形.
判定定理2：两组对角分别相等的四边形是平行四边形
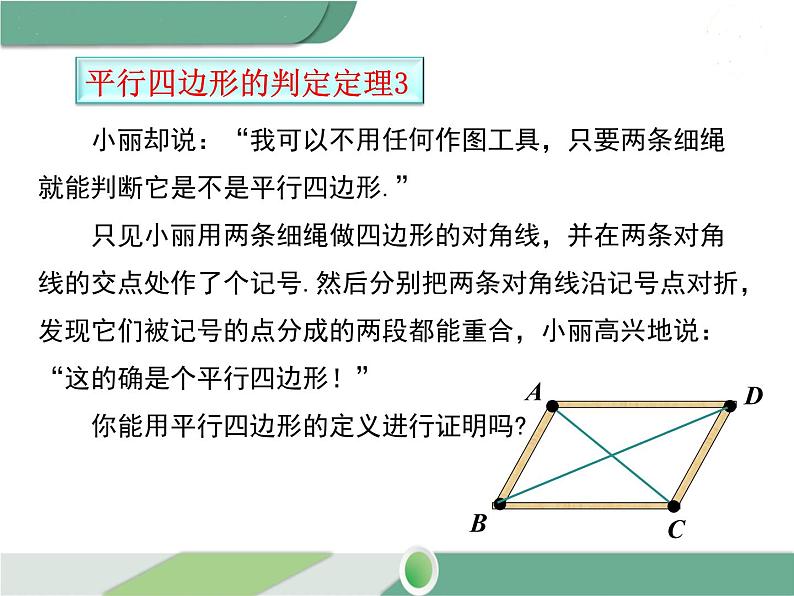
小丽却说：“我可以不用任何作图工具，只要两条细绳就能判断它是不是平行四边形.” 只见小丽用两条细绳做四边形的对角线，并在两条对角线的交点处作了个记号.然后分别把两条对角线沿记号点对折，发现它们被记号的点分成的两段都能重合，小丽高兴地说：“这的确是个平行四边形！” 你能用平行四边形的定义进行证明吗?
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO.
判定定理3：对角线互相平分的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∵AB=CD,AD=BC,∴四边形ABCD是 ABCD
∵ ∠ A= ∠ C, ∠ B= ∠ D,∴四边形ABCD是 ABCD
∵AO=CO,BO=DO,∴四边形ABCD是 ABCD
例1 填空：如图在四边形ABCD中
（1）若AB//CD，补充条件 ，使四边形ABCD为平行四边形；（2）若AB=CD，补充条件 ，使四边形ABCD为平行四边形；（3）若对角线AC、BD交于点O，OA=OC=3，OB=5，补充条件 ，使四边形ABCD为平行四边形.
解题方法：紧扣平行四边形的判定方法补上缺失条件.
（4）如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，补充条件： ,使得四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
我们知道，两组对分别平行或相等的是平行四边形。如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢？
连接AC.∵AB//CD, ∴∠1=∠2.又AB=CD，AC=CA，∴△ABC≌△CDA.∴BC=DA.∴四边形ABCD的两组对边分别相等，它是平行四边形.
已知：如图，在四边形ABCD中，AB//CD.求证：四边形ABCD是平行四边形.
一组对边平行且相等的四边形是平行四边形.
∵AB//CD，AB=CD, ∴四边形ABCD是平行四边形.
想一想：一组对边平行，另一组对边相等的四边形是不是平行四边形?如不是，请举出反例.
例2 如图，在 ABCD 中，E,F分别是AB,CD的中点，求证：四边形EBFD是平行四边形.
∵四边形ABCD是平行四边形，
∴AB=CD,EB//FD
∴四边形EBFD是平行四边形.
想一想：判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形（定义法）
两组对边分别相等的四边形是平行四边形（判定定理1）
一组对边平行且相等的四边形是平行四边形（判定定理4）
两组对角分别相等的四边形是平行四边形（判定定理2）
对角线互相平分的四边形是平行四边形（判定定理3）
1. 根据下列条件，不能判定一个四边形为平行四边形的是（ ）
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
2.能判定四边形ABCD是平行四边形的条件：∠A:∠B:∠C:∠D的值为（　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
3. 如图所示，△ABC是等边三角形，P是其内任意一点，PD//AB,PE//BC,PF//AC,若△ABC的周长为24，则PD+PE+PF= .
4.已知AD//BC ，要使这个四边形ABCD为平行四边形，需要增加条件 .
AD=BC或AB//CD
∴AB=CD,AB//CD.
∴∠ABE=∠CDF.
∴∠AEB=∠CFD=900.
∴△ABE≌△CDF.
∵ ∠AEF=∠CFE=900,
∴四边形AECF是平行四边形.