初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定优质ppt课件

这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定优质ppt课件，共31页。PPT课件主要包含了素养目标，连接中考，课后作业等内容，欢迎下载使用。

昨天初一的李明同学在生物实验室做实验时，不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校，带上玻璃剩下部分去玻璃店不安全，于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了，可原来的平行四边形怎么给它画出来呢？(A,B,C为三顶点,即找出第四个顶点D)
1. 经历并了解平行四边形的判别方法探索过程，逐步掌握说理的基本方法.
2. 掌握平行四边形的三个判定定理，能根据不同条件灵活选取适当的判定定理进行推理论证.
3. 在探索过程中发展我们的合理推理意识、培养主动探究的习惯.
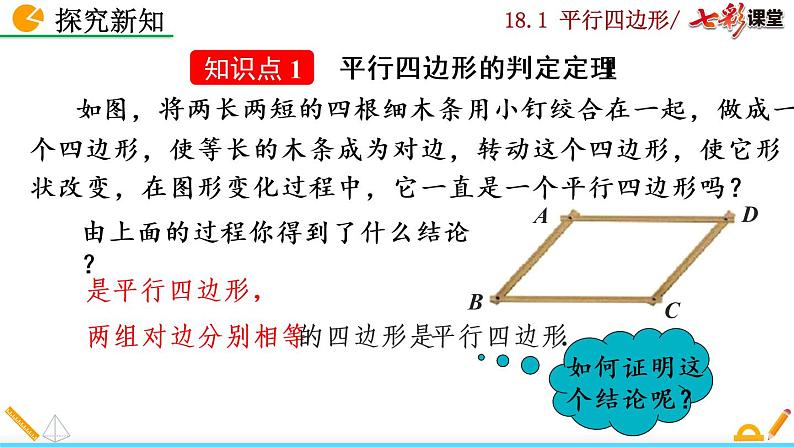
如图，将两长两短的四根细木条用小钉绞合在一起，做成一个四边形，使等长的木条成为对边，转动这个四边形，使它形状改变，在图形变化过程中，它一直是一个平行四边形吗？
由上面的过程你得到了什么结论？
是平行四边形， 两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理1
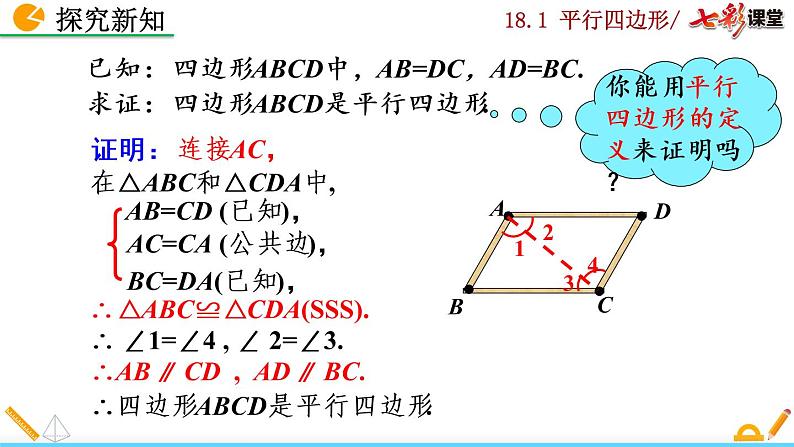
已知： 四边形ABCD中，AB=DC，AD=BC.求证： 四边形ABCD是平行四边形.
在△ABC和△CDA中,
AB=CD (已知)，
AC=CA (公共边)，
∴△ABC≌△CDA(SSS).
∴ ∠1=∠4 , ∠ 2=∠3.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
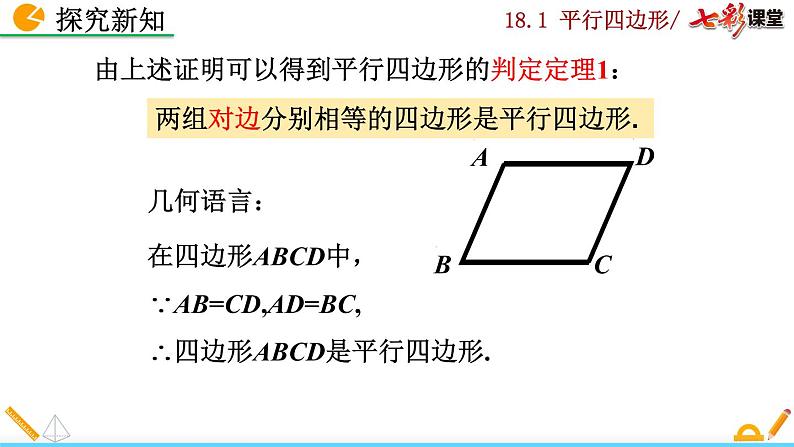
由上述证明可以得到平行四边形的判定定理1：
两组对边分别相等的四边形是平行四边形.
在四边形ABCD中，∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.
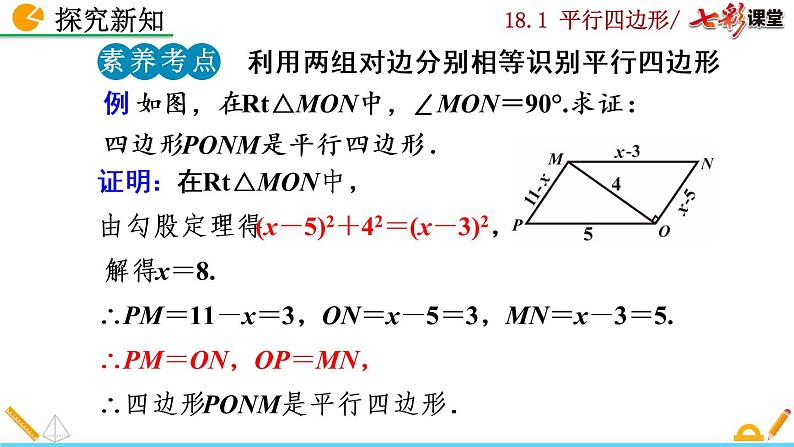
例 如图，在Rt△MON中，∠MON＝90°.求证：四边形PONM是平行四边形．
证明：在Rt△MON中，由勾股定理得(x－5)2＋42＝(x－3)2， 解得x＝8.∴PM＝11－x＝3，ON＝x－5＝3，MN＝x－3＝5.∴PM＝ON，OP＝MN，∴四边形PONM是平行四边形．
利用两组对边分别相等识别平行四边形
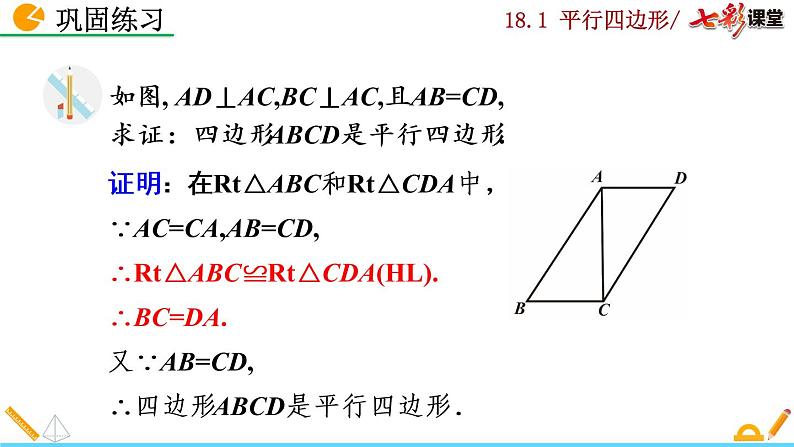
如图, AD⊥AC,BC⊥AC,且AB=CD,求证：四边形ABCD是平行四边形.
证明：在Rt△ABC和Rt△CDA中，∵AC=CA,AB=CD,∴Rt△ABC≌Rt△CDA(HL).∴BC=DA.又∵AB=CD,∴四边形ABCD是平行四边形．
一天，八年级的李明同学在生物实验室做实验时，不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校，带上玻璃剩下部分去玻璃店不安全，于是他想把原来的平行四边形重新在纸上画出来，然后带上图纸去就行了，可原来的平行四边形怎么画出来呢？
平行四边形的判定定理2
观看上面的图形，李明想使∠B=∠D，∠A=∠C即可，你觉得可以吗？对于两组对角分别相等的四边形的形状你的猜想是什么?
猜想：两组对角分别相等的四边形是平行四边形.
已知：四边形ABCD, ∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
∵∠A=∠C，∠B=∠D（已知）,
即∠A+ ∠B=180 °.
∴ AD∥BC （同旁内角互补，两直线平行）.
两组对角分别相等的四边形是平行四边形.
平行四边形的判定定理2:
∵∠A=∠C，∠B=∠D,
（两组对角分别相等的四边形是平行四边形）
例 如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.(1)求∠D的度数；(2)求证：四边形ABCD是平行四边形．
(1)解：∵∠D＋∠2＋∠1＝180°， ∴∠D＝180°－∠2－∠1＝55°；(2)证明：∵AB∥DC，∴∠2＝∠CAB.∴∠DAB＝∠1＋∠2＝125°. ∵∠DCB＋∠DAB＋∠D＋∠B＝360°，又∵∠D＝∠B＝55°，
利用平行四边形的判定定理2判定平行四边形
∴∠DCB＝∠DAB＝125°.
∴四边形ABCD是平行四边形．
判断下列四边形是否为平行四边形：
能判定四边形ABCD是平行四边形的条件： ∠A:∠B:∠C:∠D的值为 （　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
如图，将两根木条AC，BD的中点重叠，用小钉绞合在一起，用橡皮筋连接木条的顶点，做成一个四边形ABCD，转动两根木条，四边形ABCD一直是一个平行四边形吗？
对角线互相平分的四边形是平行四边形.
平行四边形的判定定理3
已知：如图，在四边形ABCD中，AC与BD相交于点O，OA=OC，OB=OD.
∴△ADO ≌△CBO.
求证：四边形ABCD是平行四边形.
在△ADO 和△CBO中，
∴ ∠1=∠2.
∵OA=OC ， OB=OD,
（对角线互相平分的四边形是平行四边形）
对角线互相平分的四边形是平行四边形.
平行四边形的判定定理3:
例 如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
利用平行四边形的判定定理3判定平行四边形
根据下列条件,不能判定四边形为平行四边形的是( )A.两组对边分别相等 B.两条对角线互相平分C.两条对角线相等 D.两组对边分别平行
如图，在四边形ABCD中，AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,BO=_____cm时，四边形ABCD是平行四边形.
1. ▱ABCD中，E，F的对角线BD上不同的两点．下列条件中，不能得出四边形AECF一定为平行四边形的是（　 ）A．BE=DF B．AE=CFC．AF∥CED．∠BAE=∠DCF
2. 平行四边形的其中一个判定定理是：两组对边分别相等的四边形是平行四边形．请你证明这个判定定理．已知：如图，在四边形ABCD中，AB＝CD，AD＝BC．求证：四边形ABCD是平行四边形．
证明：连接AC，如图所示：在△ABC和△CDA中，∴△ABC≌△CDA（SSS）.∴∠BAC＝∠DCA，∠ACB＝∠CAD.∴AB∥CD，BC∥AD.∴四边形ABCD是平行四边形．
1.如图，在四边形ABCD中，对角线AC , BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是( )A. AB∥CD，AD∥BC B. OA＝OC，OB＝ODC. AD＝BC，AB∥CD D. AB＝CD，AD＝BC
2.在四边形ABCD中，AC , BD相交于点O，（1）若AD=8cm，AB=4cm，那么当BC=___ cm， CD= ____cm时，四边形ABCD为平行四边形；（2）若AO=10cm，BO=18cm，那么当AC=___ cm， BD= ____cm时，四边形ABCD为平行四边形．
3.如图，AC∥DE且AC＝DE，AD，CE交于点B，AF，DG分别是△ABC，△BDE的中线，求证：四边形AGDF是平行四边形.
∵AC∥DE，AC＝DE，∴∠C＝∠E，∠CAB＝∠EDB.∴△ABC≌△DBE.∴AB＝DB，CB＝EB.∵AF，DG分别是△ABC，△BDE的中线，∴BG＝BF.∴四边形AGDF是平行四边形.
4.如图，已知E，F，G，H分别是▱ABCD的边AB，BC，CD，DA上的点，且AE=CG，BF=DH．求证：四边形EFGH是平行四边形．
在平行四边形ABCD中，∠A=∠C，AD=BC,又∵BF=DH，∴AH=CF.又∵AE=CG，∴△AEH≌△CGF（SAS）.∴EH=GF.同理得△BEF≌△DGH（SAS）.∴GH=EF.∴四边形EFGH是平行四边形．
如图，五边形ABCDE是正五边形，连接BD , CE，交于点P． 求证：四边形ABPE是平行四边形．
证明：∵五边形ABCDE是正五边形，∴正五边形的每个内角的度数是 AB=BC=CD=DE=AE.∴∠DEC=∠DCE= ×(180°-108°)=36°，同理∠CBD=∠CDB=36°，∴∠ABP=∠AEP=108°-36°=72°.∴∠BPE=360°-108°-72°-72°=108°=∠A.∴四边形ABPE是平行四边形．
如图，在△ABC中，分别以AB,AC,BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形．
证明：∵△ABD和△BCF都是等边三角形，∴∠DBF＋∠FBA＝∠ABC＋∠ABF＝60°. ∴∠DBF＝∠ABC.又∵BD＝BA，BF＝BC，∴△DBF≌△ABC(SAS).∴AC＝DF.又∵△ACE是等边三角形，∴AC＝DF＝AE.同理可证△ABC≌△EFC，∴AB＝EF＝AD.∴四边形DAEF是平行四边形．
定义法:两组对边分别平行的四边形叫平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形