



人教版八年级下册18.1.2 平行四边形的判定获奖ppt课件
展开1.运用类比的方法,探索平行四边形的判定方法;
2.理解平行四边形的判定方法,并会简单运用;
3.平行四边形的性质和判定的综合运用.
有两组对边分别平行的四边形叫做平行四 边形.
平行四边形的对边相等;
平行四边形的对角相等.
平行四边形的对角线互相平分.
既是平行四边形的性质也是平行四边形的判定.
你能说出这三个性质的逆命题吗?
两个命题的题设、结论正好相反,这样的两个命题叫做互逆命题.
通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
你能根据平行四边形的定义证明它们吗?
活动:探究平行四边形的判定
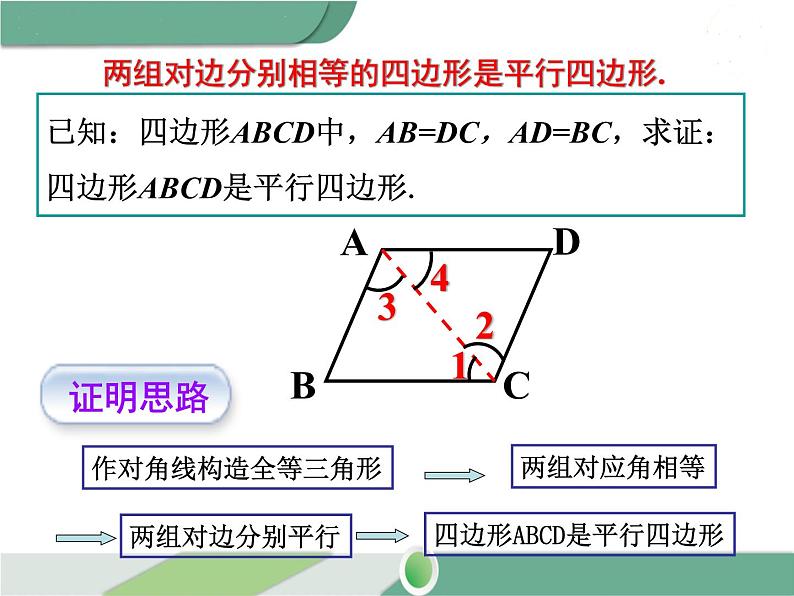
两组对边分别相等的四边形是平行四边形.
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形.
作对角线构造全等三角形
四边形ABCD是平行四边形
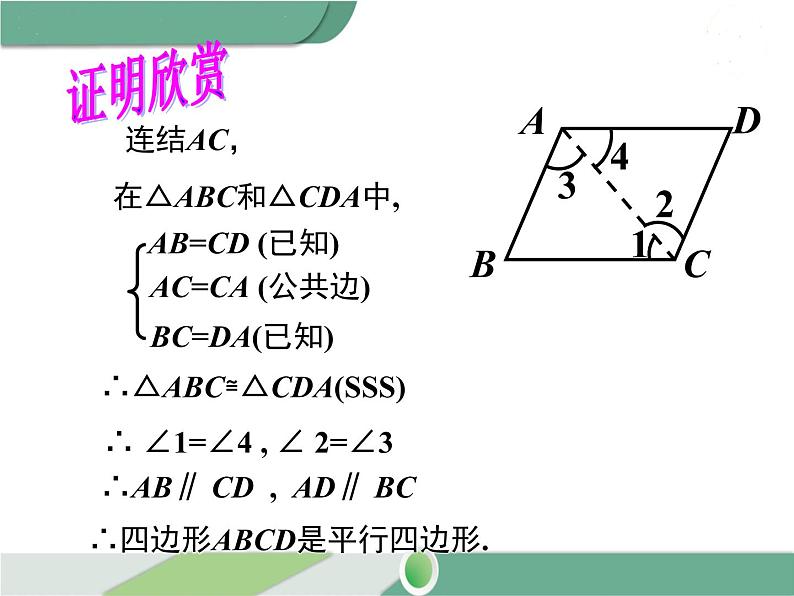
在△ABC和△CDA中,
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形.
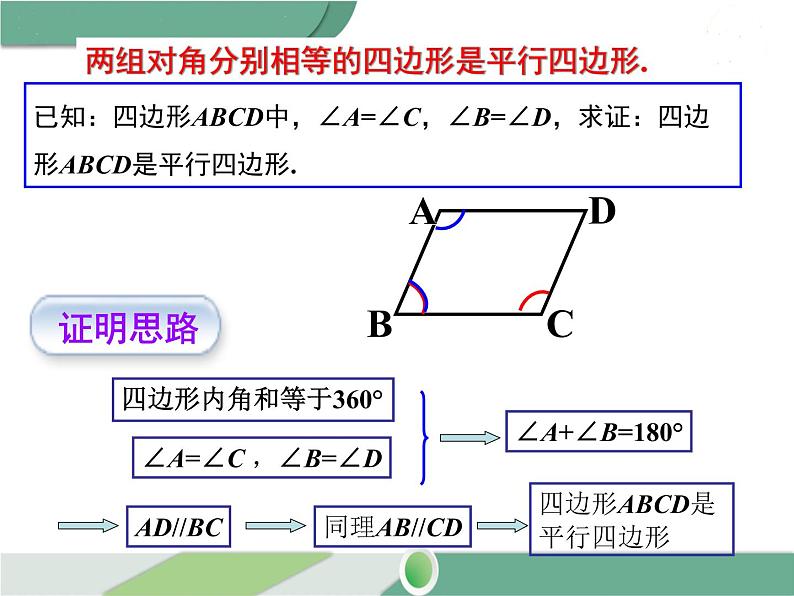
两组对角分别相等的四边形是平行四边形.
已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边 形ABCD是平行四边形.
四边形内角和等于360°
∠A=∠C ,∠B=∠D
又∵∠A=∠C,∠B=∠D
∵∠A+∠C+∠B+∠D=3600
∴2∠A+2∠B=3600
即∠A+∠B=1800
已知:四边形ABCD中,OA=OC,OB=OD,求证:四边 形ABCD是平行四边形.
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法:
定义法:两组对边分别平行的四边形是平行四边形.
判定定理2 两组对角分别相等的四边形是平行四边形.
判定定理3 两条对角线互相平分的四边形是平行四边形.
判定定理1 两组对边分别相等的四边形是平行四边形.
AB=DC AD=BC
AB∥DC AD∥BC
∠ABC=∠ADC ∠BAD=∠BCD
OA=OC OB=OD
例 填空:如图在四边形ABCD中
(1)若AB//CD,补充条件 ____,使四边形ABCD为平行四边形;(2)若AB=CD,补充条件 __,使四边形ABCD为平行四边形;(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,补充条件 ,使四边形ABCD为平行四边形.
紧扣平行四边形的判定方法补上缺失条件.
(4)已知E、F是平行四边形ABCD对角线AC上的两点,补充条件 ,使四边形BFDE是平行四边形.并请加以证明.
证明: ∵四边形ABCD是平行四边形 ∴ AO=CO,BO=DO ∵AE=CF ∴AO-AE=CO-CF ∴EO=FO 又 BO=DO ∴ 四边形BFDE是平行四边形.
1.一组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
两条对角线互相平分的四边形是平行四边形
(一)平行四边形的判定方法(1)
初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定授课课件ppt: 这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定授课课件ppt,共27页。PPT课件主要包含了学习目标,证明方法2,符号语言,链接中考,∠DAF∠E,DFCF,tcm,12-tcm,15-2tcm,平行四边形的判定等内容,欢迎下载使用。
初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定课堂教学ppt课件: 这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定课堂教学ppt课件,共13页。PPT课件主要包含了大家齐动手,行家伸伸手,平行四边形的判别方法,百炼成金,应用与拓展,想一想,尺规画平行四边形,众说纷纭,学海拾贝,收获与困惑等内容,欢迎下载使用。
初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定精品ppt课件: 这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定精品ppt课件,共18页。PPT课件主要包含了平行四边形的判定1,平行四边形的判定2,平行四边形的判定3,平行四边形的判定4,中位线,DE∥BC,DEBC,你能推理证明吗,中位线定理等内容,欢迎下载使用。













