初中数学苏科版八年级下册9.4 矩形、菱形、正方形导学案及答案

这是一份初中数学苏科版八年级下册9.4 矩形、菱形、正方形导学案及答案，共2页。学案主要包含了学习目标，学习重点、难点，课前准备，课堂研讨，课堂检测等内容，欢迎下载使用。

班级_________ 姓名____________


【学习目标】


1、经历菱形的概念、性质的发现过程；


2、掌握菱形的概念及性质定理。


3、探索菱形的对称性。


【学习重点、难点】


菱形的性质；菱形的对称性的推理过程。





【课前准备】


一、操作：如图，BO是等腰三角形ABC的底边中线，画出△ABC关于点O的中心对称图形。(把点B的对称点记作D)


思考：


（1）四边形ABCD是 图形，点O是 中心。四边形ABCD的边AB、BC之间有什么关系？.所得四边形ABCD的各边有什么特点？我们以前学过这样的四边形吗？





（2）所得四边形ABCD的对角线有什么特点？你能证明吗？





（3）归纳出：菱形概念： 的平行四边形是菱形。


二、菱形的性质


1、根据菱形的概念判断：


（1）菱形是平行四边形。 ( ) (2）平行四边形是菱形 。( )


（3）平行四边形的性质，菱形也具备。（ ）


2、根据课本P78”讨论”，把你的答案写在下面


（1）图中哪些线段相等？


哪些角相等？


（2）菱形的对角线有什么特殊的位置关系？


结论：菱形不但具备一般平行四边形的所有性质，还具备一般平行四边形没有的特殊性质：


（1）


（2） 。


思考：以上结论如何证明?








三、菱形性质的应用


1、 下列性质中，菱形具有而平行四边形不一定具有的是（ ）


A、内角和是360° B、对角相等 C、对角线互相垂直 D、对边平行


2、在菱形ABCD中，AB=3，O为对角线交点，∠,BCD=120°，则对角线AC=__ _


3、已知菱形的边长是8cm，则周长为 ；菱形的面积是4，高为1，则周长为


【课堂研讨】


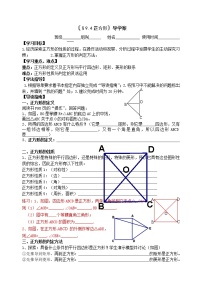
例1 如图，在菱形BCDE中，F是CD的中点，且BF⊥CD，


（1）求∠CDB的度数。 （2）若菱形边长为2，求菱形的面积。














例2 在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，求∠CDF的度数。




















【课堂检测】


A 1.已知菱形的周长是12cm，那么它的边长是______.


A 2.如下图：菱形ABCD中∠BAC＝60度，则∠BCD＝_______.


B 3、菱形的两条对角线长分别为24cm和18cm，则菱形的周长是


面积是____________


B 4、菱形ABCD 的周长为52，AC=10，则BD= .





B 5、如图，菱形ABCD的周长为20，∠DAB与∠ABC的度数之比为1:2，


对角线BD= ___ _________








C 6：已知菱形ABCD的一个内角∠BAD=80°，对角线AC、BD相交于点O，点E 在AB上，且BE=BO，求∠EOA的度数。